 |
Приложения деревьев.
|
|
|
|
Деревья имеют широкое применение при реализации трансляторов таблиц решений, при работе с арифметическими выражениями, при создании и ведении таблиц символов, где их используют для отображения структуры предложений, в системах связи для экономичного кодирования сообщений и во многих других случаях. Рассмотрим некоторые из них.
Деревья Хаффмена (деревья минимального кодирования)
Пусть требуется закодировать длинное сообщение в виде строки битов: А В А С С D А кодом, минимизирующим длину закодированного сообщения.
1) назначим коды:
| Символ | Код |
| A | |
| B | |
| C | |
| D |
Каждый символ тремя битами, получим строку:010 100 010 000 000 111 010.
А В А С С D А7*3=21 всего 21 бит - неэффективно
2) Сделаем иначе: предположим, что каждому символу назначен 2-битовый код
| Символ | Код |
| A | |
| B | |
| C | |
| D |
Тогда кодировка требует лишь 14 бит.
3) Выберем коды, которые минимизируют длину сообщения по частоте вхождений символа в строку: много вхождений - код короткий, мало вхождений - код длинный.
А -3 раза, С -2 раза, В -1 раз, D -1 раз то-есть можно:
· 1. использовать коды переменной длины.
· 2. код одного символа не должен совпадать с кодом другого (раскодирование идет слева направо).
Если А имеет код 0 т.к часто встречается, то В, С, D - начинаются с 1, если дальше 0,то это С, следующий может быть 0 или 1: 1 - D, 0 - В; то-есть В и D различаются по последнему биту, А -по первому, С - по второму, B и D - по третьему.
| Символ | Код |
| A | |
| B | |
| C | |
| D |
Таким образом, если известны частоты появления символов в сообщении, то метод реализует оптимальную схему кодирования.
Частота появления группы символов равна сумме частот появления каждого символа.
|
|
|
Сообщение АВАССDА кодируется как 0110010101110 и требует лишь 13 бит.
В очень длинных сообщениях, которые содержат символы, встречающиеся очень редко - экономия существенна.

Рис.6.30 Дерево Хаффмена
Обычно коды создаются на основе частоты во всем множестве сообщений, а не только в одном.
Деревья при работе с арифметическими выражениями
Операция объединения двух символов в один использует структуру бинарного дерева. Каждый узел содержит символ и частоту вхождения. Код любого символа может быть определен просмотром дерева снизу вверх, начиная с листа. Каждый раз при прохождении узла приписываем слева к коду 0, если поднимаемся по левой ветви и 1, если поднимаемся по правой ветви. Как только дерево построено код любого символа алфавита может быть определен просмотром дерева снизу вверх, начиная с места, представляющего этот символ. Начальное значение кода пустая строка. Каждый раз, когда мы поднимаемся по левой ветви, к коду слева приписывается ноль, если справа - 1. Часть info узла дерева содержит частоту появления символа представляемого этим узлом. Дерево Хаффмена строго бинарное. Если в алфавите п символов, то дерево Хаффмена может быть представлено массивом узлов размером 2п-1. Поскольку размер памяти, требуемой под дерево известен, она может быть выделена заранее.
МАНИПУЛИРОВАНИЕ АРИФМЕТИЧЕСКИМИ ВЫРАЖЕНИЯМИ.
Дано выражение а*(-b)+с/dОперации выполняются над выражениями, представленными в виде бинарных деревьев. Такие выражения можно символьно складывать,

Рис.6.31 Представление выражения в виде дерева

Рис. 6.32 Представление выражения в виде бинарного дерева.
перемножать, вычитать, дифференцировать, интегрировать, сравнивать на эквивалентность и т.д. Т.е. получаются символьные выражения, которые можно закодировать в виде таблиц:
· (-) - операция унарного минуса;
|
|
|
· () - операция возведения в степень;
· (+) - операция сложения;
· (*) - операция умножения;
· (/) - операция деления.
· (Е) - указательная переменная, адресующая корень дерева, каждая вершина которого состоит из левого указателя (LPТR), правого указателя (RPTR) и информационного поля TYPE.
| LPTR | DATA | RPTR |
Для неконцевой вершины поле TYPE задает арифметическую операцию, связанную с этой вершиной. Значения поля TYPE вершин +,-,*, /, (-) и равны 1, 2, 3, 4, 5, 6 соответственно.
Для концевых вершин поле символа в TYPE имеет значение 0, что означает константу или переменную. В этом случае правый указатель вершины задает адрес таблицы символов, который соответствует данной константе или переменной. В дереве указывается тип оператора, а не он сам, что позволяет упростить обработку таких деревьев.
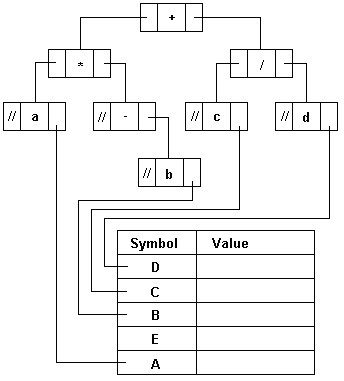
Рис.6.33 Таблица символов
Процедура вычислений:
Создается семимерный массив меток и его элементам задаются требуемые значения.Оператор генерирует метку исходя из значения поля корневой вершины. И передается управление управление оператору, помеченного меткой. Если данная вершина концевая, то в качестве значения выдается значение переменной или константы, обозначенной этой вершиной. Эта операция выполняется путем использования правого указателя данной вершины для ссылки на нужную запись в таблице символов. Для неконцевой вершины инициализируются рекурсивные вычисления ее поддеревьев, характеризующих операнды текущего оператора. Этот процесс продолжается до тех пор, пока не будут достигнуты листья дерева. Для полученных листьев значения выбираются из соответствующих записей таблицы символов.
Ниже приводится программа, вычисляющая арифметическое выражение.
|
|
|


