 |
Реологические свойства дисперсных систем. Структурная вязкость.
|
|
|
|
Структурно-механические свойства изучает реология – наука о деформациях и течении. В реологии механические свойства систем описываются с точки зрения деформаций, возникающих под действием внешних напряжений. В коллоидной химии методы реологии используются для изучения структуры и вязкостных свойств дисперсных систем.
Основными понятиями реологии являются деформация и напряжение. Под деформацией понимают относительное смещение точек системы без нарушения ее сплошности. Различают упругие и остаточные деформации. Упругие деформации обратимы, при упругой деформации после снятия приложенного напряжения структура тела полностью восстанавливается. Остаточные деформации необратимы, после снятия напряжения в структуре системы остаются изменения. Остаточные деформации, не приводящие к разрушению тела, называются пластическими.
Напряжение, под действием которого происходит деформация, определяется как отношение силы к площади, на которую эта сила действует. Напряжения, вызывающие деформации, делятся на нормальные и тангенциальные. Каждому виду напряжений соответствует определенный вид деформации. Нормальные напряжения вызывают деформации растяжения (сжатия), тангенциальные – деформации сдвига. Наиболее важными для реологических исследований являются деформации сдвига, т.к. при этих деформациях проявляются такие важнейшие свойства материальных систем как упругость, пластичность, вязкость и прочность.
П.А. Ребиндер предложил классифицировать структуры, образующиеся в дисперсных системах, по характеру взаимодействия частиц. В соответствии с этим различают конденсационно-кристаллизационные и коагуляционные структуры. При срастании частиц образуются конденсационно-кристаллизационные структуры, обладающие жесткой структурой и высокой прочностью. Коагуляционные структуры образуются в случае контактирования частиц через прослойку дисперсионной среды. Для систем с коагуляционными структурами характерно восстановление структуры во времени после ее механического разрушения. Это явление получило название тиксотропии.
|
|
|
По реологическим свойствам все реальные системы делят на жидкообразные и твердообразные. К жидкообразным системам относятся системы с пределом текучести равным нулю (q = 0), к твердообразным – с q > 0.
Жидкообразные системы делят на ньютоновские и неньютоновские. Ньютоновскими называют системы, подчиняющиеся закону Ньютона. Вязкость ньютоновских жидкостей не зависит от напряжения сдвига.
При перемещении жидкости по узким трубкам отдельные ее слои передвигаются с различными скоростями, возрастающими от стенок к центру (рисунок 5.1). Между слоями текущей жидкости возникает сила внутреннего трения F тр.равная, согласно закону Ньютона:
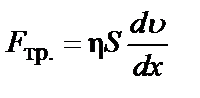 , (5.1)
, (5.1)
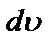 – изменение скорости абсолютной деформации между двумя слоями жидкости, находящимися на расстоянии dx;
– изменение скорости абсолютной деформации между двумя слоями жидкости, находящимися на расстоянии dx;
h – коэффициент пропорциональности;
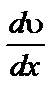 – градиент скорости абсолютной деформации жидкости.
– градиент скорости абсолютной деформации жидкости.
Разделив обе части уравнения (5.1) на площадь S, получим
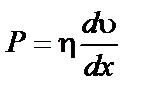 , (5.2)
, (5.2)
где Р – напряжение сдвига, то есть сила, отнесенная к единице площади поверхности трущихся слоев. При 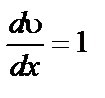 P= h, тогда h принимает смысл напряжения сдвига при градиенте скорости сдвига равном единице; и носит название коэффициента внутреннего трения или динамической вязкости.
P= h, тогда h принимает смысл напряжения сдвига при градиенте скорости сдвига равном единице; и носит название коэффициента внутреннего трения или динамической вязкости.
|
|
|
Из уравнения (5.2) вытекает размерность динамической вязкости 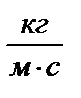 . Единицей вязкости в системе СИ является Па × с (паскаль-секунда); в системе СГC - пуаз (пз) (1 пз = 0,1 Па × с). Для маловязких жидкостей пользуются величиной мПа × с (миллипаскаль-секунда). Например, динамическая вязкость воды при 20°С равна 1,002 мПа × с (1 мПа × с = 1 спз).
. Единицей вязкости в системе СИ является Па × с (паскаль-секунда); в системе СГC - пуаз (пз) (1 пз = 0,1 Па × с). Для маловязких жидкостей пользуются величиной мПа × с (миллипаскаль-секунда). Например, динамическая вязкость воды при 20°С равна 1,002 мПа × с (1 мПа × с = 1 спз).
Непосредственное использование закона Ньютона для расчета вязкости затруднительно в силу сложности экспериментального определения градиента скорости. Обычно для этого применяют уравнение Пуазейля для истечения жидкости из узких трубок (капилляров)
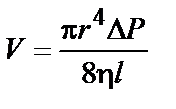 , (5.3)
, (5.3)
где V – объемная скорость истечения; r – радиус капилляра;  – перепад давления, под действием которого жидкость вытекает из капилляра; l – длина капилляра; h – вязкость жидкости.
– перепад давления, под действием которого жидкость вытекает из капилляра; l – длина капилляра; h – вязкость жидкости.
Уравнения Ньютона и Пуазейля справедливы только для ламинарного режима течения жидкости. Жидкости, подчиняющиеся законам Ньютона и Пуазейля, называются нормальными или ньютоновскими; жидкости, способные течь, но не подчиняющиеся этим уравнениям, принято называть аномальными или неньютоновскими.
Присутствие в жидкости частиц коллоидной степени дисперсности увеличивает вязкость. Связь между вязкостью системы h и концентрацией дисперсной фазы установил, исходя из чисто гидродинамических соображений, Эйнштейн:
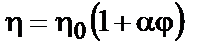 , (5.4)
, (5.4)
где  – вязкость дисперсионной среды;
– вязкость дисперсионной среды;
a– константа, зависящая от формы частиц дисперсной фазы (для сферических частиц a= 2,5); j– объемная доля дисперсной фазы в системе.
Уравнение (5.4) применимо только к разбавленным растворам, где частицы не оказывают влияния друг на друга и при условии ламинарного режима течения.
Однако в некоторых случаях даже при сравнительно небольших концентрациях лиофильного золя (например, разбавленные гидрозоли желатина, таннина, 0,0045 % –гидрозоль пятиокиси ванадия, 0,1% раствор бентонита в воде и др.), линейная зависимость, определяемая уравнением (5.4), нарушается, и вязкость оказывается значительно более высокой, чем это следует из уравнения.
Последнее обстоятельство объясняется, во-первых, тем, что эти золи могут легко переходить в гели и в системе появляется пространственная структура. Во-вторых, частицы коллоидов, взаимодействуя с дисперсионной средой, приобретают сольватные оболочки, что ведет к увеличению эффективного объема частиц.
|
|
|
При наличии в системе малопрочной пространственной структуры, способной разрушаться в вискозиметре, течение начинается лишь тогда, когда напряжение сдвига P превысит некоторое определенное критическое значение q, необходимое для. разрушения структуры, то есть, когда будет соблюдаться условие
Р – q > 0.
Такое течение называется пластическим, а критическое (предельное) напряжение сдвига q– пределом текучести. Для таких систем уравнение Ньютона заменяется уравнением Шведова-Бингама
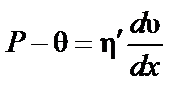 , (5.5)
, (5.5)
где  – вязкость, отвечающая так называемому пластическому течению системы.
– вязкость, отвечающая так называемому пластическому течению системы.
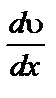 от напряжения сдвига P: 1 – ньютоновская жидкость, 2 – система Шведова-Бингама, 3 – система с прочной пространственной структурой, разрушающейся по мере роста напряжения сдвига сдвига от напряжения сдвига P: 1 – ньютоновская жидкость, 2 – система Шведова-Бингама, 3 – система с прочной пространственной структурой, разрушающейся по мере роста напряжения сдвига сдвига
|
В структурированных жидкостях течение с постоянной вязкостью начинается, когда напряжение сдвига Р превысит q (прямая 2 в системе координат  , рисунок 5.2).
, рисунок 5.2).
Отсюда пластическая вязкость
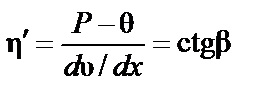 . (5.6)
. (5.6)
Примером систем, подчиняющихся уравнению Шведова-Бингама, являются пасты из глины (глинистые растворы или промывочные жидкости), консистентные смазки, некоторые краски.
На основе уравнения Шведова-Бингама создана гидравлика глинистых растворов, позволяющая решать важные теоретические и практические задачи, связанные с расчетом потерь напора в циркуляционной системе, правильного подбора насосов и др.
Системы, подчиняющиеся уравнению Шведова-Бингама, называются бингамовскими. Для них характерно явление тиксотропии – изотермического перехода структурированной системы под действием сдвигового напряжения Р в бесструктурную и восстановление структуры после прекращения воздействия сдвигового напряжения.
|
|
|
Однако в большинстве случаев зависимость 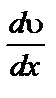 от Р выражается не прямой, а кривой 3 (рисунок 5.2); при достижении предела текучести структура разрушается не сразу, а постепенно по мере увеличения напряжения сдвига P.
от Р выражается не прямой, а кривой 3 (рисунок 5.2); при достижении предела текучести структура разрушается не сразу, а постепенно по мере увеличения напряжения сдвига P.
В этом случае различают три критических напряжения сдвига: qmin– минимальный предел текучести, соответствующий началу течения или разрушения структуры; qВ– предел текучести по Шведову-Бингаму; qmах –максимальный предел текучести, соответствующий значению напряжения, при котором кривая переходит в прямую, в этот момент структура полностью разрушена, и система течет как ньютоновская жидкость.
Как уже указывалось, в большинстве случаев структурированные системы изменяются постепенно и только после полного разрушения структуры текут как ньютоновские.
По реологическому поведению к бингамовским системам относятся пульпы, шламы, зубные пасты, масляные краски, пластичные смазки.
В качестве моделей структурированных систем рассмотрим поведение водного раствора КМЦ и толуольного раствора каучука при их продавливании через капилляр вискозиметра.
На рисунке 5.4 a показана модель структуры водного раствора КМЦ, представляющая собой "кучу хвороста", где роль ''хвороста" выполняют относительно небольшие макромолекулы КМЦ и структура "клубок ниток" (рисунок 5.4 b), образованная огромными и гибкими по сравнению с КМЦ макромолекулами каучука. Дисперсионной средой в этих системах являются соответственно вода и толуол. При приложении внешнего давления начинается постепенное "разрушение" структуры, выражающееся в упорядочении движения макромолекул. Структура считается разрушенной полностью, когда макромолекулы при их протекании через капилляр начинают двигаться упорядоченно, располагаясь вдоль оси капилляра – в этот момент указанные системы ведут себя как ньютоновские жидкости.
|
|
|
Вязкость жидкостей и дисперсных систем определяют различными методами: а) методом падающего шарика (вискозиметр Гепплера); б) методом истечения жидкости из капилляра (вискозиметр Оствальда, вискозиметр СПВ-5, используемый в нефтепромысловой практике); в) методом определения вязкостных характеристик с помощью ротационных и торсионных вискозиметров (вискозиметры Куэтта, Воларовича, СНС-2, Реотест-2 и др.).
При работе с капиллярным вискозиметром имеется простой способ выяснения вопроса, является ли исследуемая жидкость ньютоновской или неньютоновской. Для этого избыточное давление,под которым вытекает жидкость, умножают на соответствующее время истечения.
Представим уравнение Пуазейля в виде:
 . (5.7)
. (5.7)
Если произведение  не зависит от давления, под которым происходит истечение, жидкость является ньютоновской, если же зависит – жидкость аномальная, неньютоновская.
не зависит от давления, под которым происходит истечение, жидкость является ньютоновской, если же зависит – жидкость аномальная, неньютоновская.
Вязкость жидкостей существенно зависит от температуры. Для большинства жидкостей зависимость вязкости от температуры при постоянном давлении в узком интервале температур может быть описана уравнением:
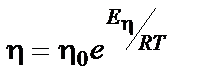 , (5.8)
, (5.8)
где h0 – предэкспоненциальный множитель, слабо зависящий от температуры; Е h – энергия активации вязкого течения.
Учитывая сильную зависимость вязкости жидкостей от температуры, эксперименты по изучению их реологического поведения проводят в условиях термостатирования исследуемой системы.
Лабораторная работа 5. 1
|
|
|


