 |
Закон гей- люссака (изобарный процесс)
|
|
|
|
ЗАКОН БОЙЛЯ-МАРИОТТА (ИЗОТЕРМИЧЕСКИЙ ПРОЦЕСС)
Некоторые простые закономерности, связывающие между собой параметры состояния газообразного вещества, были эмпирически открыто сравнительно давно. В середине 17-го века англичанин Р. Бойль и француз Э. Мариотт независимо друг от друга открыли закон, которому подчиняется изменение давления газа P при изменении объема V, если при этом температура T остается постоянной. Согласно закону, носящему их имя, при постоянной температуре для данной массы газа произведение объема, занимаемого газом, на его давление является постоянной величиной.
Рассмотрим газ в условиях, когда его температура поддерживается постоянной (такие условия называются изотермическими). Если в уравнений состояния PV=mRT/M положить T=const, то ясно, что вся правая часть уравнения оказывается величиной постоянной, так что
PV=const. (1)
Эта формула, которую называют уравнением изотермы, и выражает закон Бойля-Мариотта, согласно которому при постоянной температуре сжатие и расширение газа, т.е изменение его объема, сопровождается таким изменением давления, что произведение давления на объем остается величиной постоянной. Графически зависимость P от V для различных температур изображена нарисунке, который находится ниже 
.
Из формулы (1) видно, что эти кривые, называемые изотермами, представляют собой гиперболы.
Закон Бойля-Мариотта показывает как изменяется давление газа с изменением его объема при постоянной температуре и, конечно, при неизменной массе.
Закон Бойля — Мариотта утверждает, что давление газа в изотермическом процессе обратно пропорционально занимаемому газом объёму. Если учесть, что плотность газа[6] также обратно пропорциональна занимаемому им объёму, то мы придём к заключению:
|
|
|
При изотермическом процессе давление газа изменяется прямо пропорционально его плотности.
Известно, что сжимаемость, то есть способность газа изменять свой объём под действием давления, характеризуется коэффициентом сжимаемости [7]. В случае изотермического процесса говорят об изотермическом коэффициенте сжимаемости, который определяется формулой
{\displaystyle \beta _{T}=-{\frac {1}{V}}\left({\frac {\partial V}{\partial p}}\right)_{T},}
где индекс T означает, что частная производная берётся при постоянной температуре. Подставляя в эту формулу выражение для связи давления и объёма из закона Бойля — Мариотта, получаем[5]:
{\displaystyle \beta _{T}={\frac {1}{p}}.}
Таким образом, приходим к выводу:
Изотермический коэффициент сжимаемости идеального газа равен обратной величине его давления.
Нетрудно вычислить работу при изотермическом расширении идеального газа. Пусть исходное состояние газа имеет координаты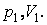 
Тогда из уравнения изотермы 
следует, что
|
Подставляя последнее соотношение в определение работы 
, получим
|
Используя уравнение изотермы , нетрудно выражение для работы (4.6.4) представить в следующем виде:
|
На основании соотношения (4.6.2) формулы (4.6.3–4.6.4) пригодны и для вычисления количества тепла, необходимого для изотермического расширения или сжатия идеального газа.
ЗАКОН ГЕЙ- ЛЮССАКА (ИЗОБАРНЫЙ ПРОЦЕСС)
Закон Гей-Люссака — закон пропорциональной зависимости объёма газа от абсолютной температуры при постоянном давлении, названный в честь французского физика и химика Жозефа Луи Гей-Люссака, впервые опубликовавшего его в 1802 году.
Следует отметить, что в англоязычной литературе закон Гей-Люссака обычно называют законом Шарля и наоборот. Кроме того, законом Гей-Люссака называют также химический закон объёмных отношений.
|
|
|
Неоднозначность терминологии связана с историей открытия газовых законов. Закон объёмов (называемый в русскоязычной литературе законом Гей-Люссака) впервые был опубликован в открытой печати в 1802 году Гей-Люссаком[1], однако сам Гей-Люссак считал, что открытие было сделано Жаком Шарлем в неопубликованной работе, относящейся к 1787 году. Независимо от них закон был открыт в 1801 году английским физиком Джоном Дальтоном. Кроме того, качественно закон был описан французом Гийомом Амонтоном в конце XVII века. В любом случае, Гей-Люссак первым продемонстрировал, что закон справедлив не только для воздуха, но и для других газов и паров. (На самом деле пары весьма приближенно подчиняются газовым законам).
Пусть теперь газ находится в условиях, когда постоянным сохраняется его давление, но изменяется температура. Такие условия можно осуществить, если поместить газ в цилиндр, закрытый подвижным поршнем. В таком цилиндре изменение температуры вызывает перемещение поршня и изменение объема. Давление же остается постоянным.
Из уравнения Менделеева-Клапейрона видно, что в этом случае постоянным будет отношение объема газа к его температуре:
Это уравнение, называемое уравнением изобары (процесс, происходящий при постоянным давлении, называется изобарическим), выражает известный закон Гей-Люссака (иногда его называют, без достаточных, впрочем,, оснований, законом Шарля).
График изобары, как это видно из (2), имеет вид прямой, исходящей из начала координат.
Согласно закону объёмных отношений, если два газа участвуют в химической реакции, то отношение их объёмов, измеренных при одинаковой температуре и давлении, образует дробь, числитель и знаменатель которой являются небольшими целыми числами.
Этот закон отражает тот факт, что
· одинаковые объёмы газов при одинаковых температуре и давлении содержат одинаковые количества молекул;
· в химической реакции участвует целое количество молекул и на одну молекулу вещества приходится одинаковое количество молекул другого вещества (стехиометрия химической реакции), которое определяется коэффициентами уравнения реакции.
Работа газа при изобарном расширении или сжатии выражается соотношением
|
|
|
| A = P (V 2 – V 1) = P Δ V. |
Первый закон термодинамики для изобарного процесса записывается в виде
| Q = U (T 2) – U (T 1) + P (V 2 – V 1) = Δ U + P Δ V. |
Здесь U (T 1) и U (T 2) – внутренняя энергия газа в начальном и конечном состояниях, V 1 и V 2 – начальный и конечный объемы. При изобарном расширении Q > 0 – тепло поглощается, и газ совершает положительную работу. При изобарном сжатии Q > 0 – тепло отдается внешним телам. В этом случае A < 0.
В модели можно выбирать давление газа и проводить процесс при выбранном давлении. Приводится график зависимости V (T) для изобарного процесса, выводится энергетическая диаграмма, на которой указываются количество теплоты Q, полученной газом, произведенная работа A и изменение Δ U его внутренней энергии.
При помощи энергетической диаграммы вы также можете убедиться, что при изобарном расширении внутренняя энергия газа увеличивается (при этом его температура растет), и газ совершает положительную работу. При изобарном сжатии температура и внутренняя энергия уменьшаются, работа газа отрицательна. Также из диаграммы видно, что при расширении газ поглощает тепло, а при сжатии – отдает окружающим телам.
|
|
|
