 |
Закон Шарля (изохорический процесс)
|
|
|
|
Зако́н Ша́рля или второй закон Гей-Люссака — один из основных газовых законов, описывающий соотношение давления и температуры для идеального газа. Экспериментальным путём зависимость давления газа от температуры при постоянном объёме установлена в 1787 году Шарлем и уточнена Гей-Люссаком в 1802 году.
Изохорический или изохорный процесс (от др.-греч. ἴσος — «равный» и χώρος — «место») — термодинамический процесс, который происходит при постоянном объёме. Для осуществления изохорного процесса в газе или жидкости достаточно нагревать (охлаждать) вещество в сосуде, который не изменяет своего объёма.
При изохорическом процессе давление идеального газа прямо пропорционально его температуре (см. Закон Шарля). В реальных газах закон Шарля не выполняется.
На графиках изображается линиями, которые называются изохоры. Для идеального газа они являются прямыми во всех диаграммах, которые связывают параметры: {\displaystyle T} (температура), {\displaystyle V} (объем) и {\displaystyle P} (давление).
Наиболее часто первые исследования изохорного процесса связывают с Гильомом Амптоном. В своей работе «Парижские мемуары» в 1702 году он описал поведение газа в фиксированном объёме[Комм 1] внутри так называемого «воздушного термометра». Жидкость в нём находится в равновесии под воздействием давления газа в резервуаре и атмосферным давлением. При нагревании давление в резервуаре увеличивается, и жидкость вытесняется в выступающий столб. Зависимость между температурой и давлением была установлена в виде:
{\displaystyle {\frac {p_{1}}{p_{2}}}={\frac {1+\alpha t_{1}}{1+\alpha t_{2}}}}
В 1801 году Джон Дальтон в двух своих эссе опубликовал эксперимент, в котором установил, что все газы и пары, исследованные им при постоянном давлении, одинакового расширяются при изменении температуры, если начальная и конечная температура одинакова[2][3]. Данный закон получил название закона Гей-Люссака, так как Гей-Люссак, вскоре провёл самостоятельные эксперименты и подтвердил одинаковое расширение различных газов, причём получив практически тот же самый коэффициент, что и Дальтон[3]. Впоследствии он же объединил свой закон с законом Бойля — Мариотта[4], что позволило описывать в том числе и изохорный процесс.
|
|
|
Изменение давления газа при изменении его температуры происходит так, что отношение P/T остается постоянным:
Это утверждение, однако, нельзя считать законом природы. Температурная шкала идеального газа строится именно на основе предположения, что
. Поэтому экспериментальная проверка этого закона не может дать иного результата.
В изохорном процессе (V = const) газ работы не совершает, A = 0.
АДИАБАТИЧЕСКИЙ ПРОЦЕСС
Адиабати́ческий, или адиаба́тный проце́сс (от др.-греч. ἀδιάβατος — «непроходимый») — термодинамический процесс в макроскопической системе, при котором система не обменивается теплотой с окружающим пространством. 
Серьёзное исследование адиабатических процессов началось в XVIII веке[1].
Адиабатический процесс является частным случаем политропного процесса, так как при нём теплоёмкость газа равна нулю и, следовательно, постоянна[2]. Адиабатические процессы обратимы только тогда, когда в каждый момент времени система остаётсяравновесной (например, изменение состояния происходит достаточно медленно) и изменения энтропии не происходит. Некоторые авторы (в частности, Л. Д. Ландау) называли адиабатическими только обратимые адиабатические процессы[3].
Обратимый адиабатический процесс для идеального газа описывается уравнением Пуассона. Линия, изображающая адиабатный процесс на термодинамической диаграмме, называется адиабатой Пуассона. Примером необратимого адиабатического процесса может быть распространение ударной волны в газе. Такой процесс описывается ударной адиабатой. Адиабатическими можно считать процессы в целом ряде явлений природы. Также такие процессы получили ряд применений в технике.
|
|
|
Существование атмосферного давления было показано рядом экспериментов в XVII веке. Одним из первых доказательств гипотезы стали магдебургские полушария, сконструированные немецким инженером Герике. Из сферы, образованной полушариями, выкачивался воздух, после чего их было трудно разъединить в силу внешнего давления воздуха. Другой эксперимент в рамках исследования природы атмосферного давления поставил Роберт Бойль. Он состоял в том, что если запаять изогнутую стеклянную трубку с короткого конца, а в длинное колено постоянно подливать ртуть, она не поднимется до верха короткого колена, поскольку воздух в трубке, сжимаясь, будет уравновешивать давление ртути на него. К 1662 году данные опыты позволили прийти к формулировке закона Бойля — Мариотта[4].
В 1779 году в «Пирометрии» Ламберта был описан опыт повышения и понижения температуры в приёмнике воздушного насосапри движении поршня. Впоследствии данный эффект был подтверждён Дарвином (1788) и Пикте (1798). В 1802 году Дальтонопубликовал доклад, в котором, в числе прочего, указал, что сгущение газов сопровождается выделением тепла, а разрежение — охлаждением. Рабочий оружейного завода зажёг трут в дуле духового ружья путём сжатия воздуха, о чём сообщил в 1803 году лионский физик Моле[1].
Теоретическим обобщением накопившихся экспериментальных знаний занялся физик Пуассон. Так как при адиабатическом процессе температура непостоянна, то закон Бойля — Мариотта требует поправки, которую Пуассон обозначил как коэффициент k и выразил через соотношение теплоёмкостей. Экспериментально данный коэффициент определялся Вальтером и Гей-Люссаком (эксперимент описан в 1807 году) и затем, более точно Дезормом и Клеманом в 1819 году. Практическое использование адиабатического процесса предложил С. Карно в работе «Движущая сила огня» в 1824 году.
|
|
|
Если термодинамический процесс в общем случае представляет собой три процесса — теплообмен, совершение системой (или над системой) работы и изменение её внутренней энергии[5], то адиабатический процесс в силу отсутствия теплообмена (dQ=0{\displaystyle \Delta Q=0}) системы со средой сводится только к последним двум процессам[6]. Поэтому, первое начало термодинамики в этом случае приобретает вид dU=-A
{\displaystyle \Delta U=-A,}
Где dU {\displaystyle \Delta U} — изменение внутренней энергии тела, dA{\displaystyle A} — работа, совершаемая системой.
Изменения энтропии {\displaystyle S}dS системы в обратимом адиабатическом процессе вследствие передачи тепла через границы системы не происходит[8]: dS=dQ/T=0
{\displaystyle \mathrm {d} S=\delta Q/T=0.}
Здесь {\displaystyle T}T — температура системы, {\displaystyle \delta Q}dQ — теплота, полученная системой. Благодаря этому адиабатический процесс может быть составной частью обратимого цикла.
Открытие адиабатического процесса практически сразу нашло применение в дальнейших исследованиях. Создание теоретической модели цикла Карно позволило установить пределы развития реальных тепловых машин (сам С. Карно показал, что двигатель с более высоким КПД позволил бы создать вечный двигатель[25]). Однако цикл Карно трудно осуществим для некоторых реальных процессов, так как входящие в его состав изотермы требуют определённой скорости теплообмена[26]. Поэтому были разработаны принципы циклов, частично сходных с циклом Карно (например, цикл Отто, цикл сжижения газа), которые были бы применимы в конкретных практических задачах.
Дальнейшие исследования показали также, что некоторые процессы в природе (например, распространение звука в газе) можно с достаточной степенью приближения описывать адиабатическим процессом и выявлять их закономерности[27]. Химическая реакция внутри объёма газа в случае отсутствия теплообмена с окружающей средой также по определению будет адиабатическим процессом. Таким процессом является, например, адиабатическое горение. Для атмосферы Земли также считается адиабатическим процесс совершения газом работы на увеличение его потенциальной энергии. Исходя из этого, можно определить адиабатический градиент температуры для атмосферы Земли[28]. Теория адиабатического процесса употребляется и для других астрономических объектов с атмосферой. В частности, для Солнца наличие макроскопических конвекционных движений теоретически определяют путём сравнения адиабатического градиента и градиента лучевого равновесия[29]. Адиабатическими можно считать процессы, происходящие с применением адиабатных оболочек.
|
|
|
Цикл Карно является идеальным термодинамическим циклом. Тепловая машина Карно, работающая по этому циклу, обладает максимальным КПД из всех машин, у которых максимальная и минимальная температуры осуществляемого цикла совпадают соответственно с максимальной и минимальной температурами цикла Карно[8][30].
Максимальное КПД достигается при обратимом цикле[8]. Для того, чтобы цикл был обратимым, из него должна быть исключена передача тепла при наличии разности температур. Чтобы доказать этот факт, предположим, что передача тепла при разности температур имеет место. Данная передача происходит от более горячего тела к более холодному. Если предположить процесс обратимым, то это означало бы возможность передачи тепла обратно от более холодного тела к более нагретому, что невозможно, следовательно процесс необратим[26]. Соответственно, преобразование тепла в работу может происходить только изотермически[Комм 3]. При этом обратный переход двигателя в начальную точку только путём изотермического процесса невозможен, так как в этом случае вся полученная работа будет затрачена на восстановление исходного положения. Так как выше было показано, что адиабатический процесс может быть обратимым — то этот вид адиабатического процесса подходит для использования в цикле Карно.
Всего при цикле Карно происходят два адиабатических процесса[30]:
1. Адиабатическое (изоэнтропическое) расширение (на рисунке — процесс 2→3). Рабочее тело отсоединяется от нагревателя и продолжает расширяться без теплообмена с окружающей средой. При этом его температура уменьшается до температуры холодильника.
2. Адиабатическое (изоэнтропическое) сжатие (на рисунке — процесс 4→1). Рабочее тело отсоединяется от холодильника и сжимается без теплообмена с окружающей средой. При этом его температура увеличивается до температуры нагревателя.
ПОЛИТРОПНЫЙ ПРОЦЕСС
Политропным называют процесс, который описывается уравнением
| PVn = const, |
где n - показатель политропы.
Политропный процесс протекает при постоянной теплоемкости.
|
|
|
Найдем молярную теплоемкость Сn идеального газа в политропном процессе.
Согласно первому началу термодинамики
 .
|
Уравнение состояния одного моля идеального газа
| PV = RT. |
Решив совместно (3.35) и (3.37), получим
| TVn-1=const. |
Дифференцируем уравнение (3.38):
| (n-1)TVn-1dV+Vn-1dT=0. |
Преобразуем последнее выражение к виду
 .
|
Правую часть равенства (3.40) подставим в (3.36). Тогда
|
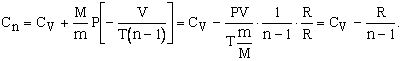
После подстановки выражения 
в (3.41) окончательно получим, что теплоемкость политропного процесса
|
Политропный процесс является обобщением всех изопроцессов.
Замечание: 1. Изобарический процесс, Р=сonst. В этом случае уравнение политропы PVn = const принимает вид PV0 = const, т.к. показатель политропы n=0, Cn=Cp.
2. Изотермический процесс, Т=сonst. При n=1 уравнение политропы переходит в уравнение изотермы, т.е. PV=сonst. Теплоемкость при постоянной температуре согласно (3.42) Cn=CT =±¥.
3. Изохорический процесс, V=сonst. При n=±¥ уравнение политропы переходит в уравнение изохоры.
Теплоемкость при постоянном объеме 
.
4. Адиабатический процесс, Q=сonst. При n=g уравнение политропы переходит в уравнение адиабаты, а теплоемкость Cn=CQ=0.
Найдем работу политропного процесса.
Рассмотрим два адиабатических состояния:
 .
|
Из (3.43) найдем давление
 .
|
Работа политропного процесса
 .
|
|
|
|
