Расчет сталефибробетонных элементов на продавливание при действии сосредоточенных силы и изгибающего момента

6.6.4 Расчет сталефибробетонных элементов на продавливание при совместном действии сосредоточенных силы и изгибающего момента, при фибровом армировании (рис. 6.13) производят из условия:

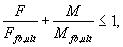(6.92)

где F - сосредоточенная сила от внешней нагрузки;

М - сосредоточенный изгибающий момент от внешней нагрузки, учитываемый при расчете на продавливание (п. 6.6.1);

F_{fb , ult} и M_{fb , ult} - предельные сосредоточенные сила и изгибающий момент, которые могут быть восприняты сталефибробетоном в расчетном поперечном сечении при их раздельном действии.

В сталефибробетонном каркасе зданий с плоскими перекрытиями сосредоточенный изгибающий момент М_lос равен суммарному изгибающему моменту в сечениях верхней и нижней колонн, примыкающих к перекрытию в рассматриваемом узле.

Предельную силу F_{fb , ult} определяют согласно п. 6.6.2.

Предельный изгибающий момент М_{fb , ult} определяют по формуле;

М_{fb , ult} = R_fbtW_fbh, (6.93)

где W_fb - момент сопротивления расчетного контура поперечного сечения, определяемый согласно п. 6.6.6.

При действии изгибающих моментов в двух взаимно перпендикулярных плоскостях расчет производят из условия:

_{0675S10-02602}

(6.94)

где F, M_x и M_y - сосредоточенные сила и изгибающие моменты в направлениях осей X и Y, учитываемые при расчете на продавливание (п. 6.6.1), от внешней нагрузки;

F_{fb , ult} , M_{fbx , ult} и M_{fby , ult} - предельные сосредоточенные сила и изгибающие моменты в направлениях осей X и Y, которые могут быть восприняты сталефибробетоном в расчетном поперечном сечении при их раздельном действии.

Усилие F_{fb , ult} определяют согласно п. 6.6.2.

Усилия M_{fbx , ult} и M_{fby , ult} определяют согласно указаниям, приведенным выше, при действии момента соответственно в плоскости оси X и в плоскости оси Y.

При расположении сосредоточенной силы внецентренно относительно центра тяжести контура расчетного поперечного сечения значения изгибающих сосредоточенных моментов от внешней нагрузки определяют с учетом дополнительного момента от внецентренного приложения сосредоточенной силы относительно центра тяжести контура расчетного поперечного сечения.

0675S10-02602

1 - расчетное поперечное сечение; 2 - контур расчетного поперечного сечения; 3 - границы зоны, в пределах которых в расчете учитывается поперечная арматура; 4 - контур расчетного поперечного сечения без учета в расчете поперечной арматуры; 5 - контур площадки приложения нагрузки

Рисунок 6. 14 - Схема для расчета сталефибробетонных плит с вертикальной равномерно распределенной поперечной арматурой на продавливание

6.6.5 Расчет сталефибробетонных элементов на продавливание при действии сосредоточенных силы и изгибающего момента при комбинированном армировании (рис. 6.14) производят из условия:

_{0675S10-02602}

(6.95)

где F и M - по п. 6.6.4;

F_{fb , ult} и M_{fb , ult} - предельные сосредоточенные сила и изгибающий момент, которые могут быть восприняты сталефибробетоном в расчетном поперечном сечении при их раздельном действии;

F_{sw , ult} и M_{sw , ult} - предельные сосредоточенные сила и изгибающий момент, которые могут быть восприняты поперечной арматурой при их раздельном действии.

Усилия F_{fb , ult} , M_{fb , ult} и F_{sw , ult} определяют согласно пп. 6.6.3 и 6.6.4.

Усилие M_{sw , ult}, воспринимаемое поперечной арматурой, нормальной к плоскости элемента и расположенной равномерно вдоль контура расчетного сечения, определяют по формуле:

M_{sw , ult} = 0,8 q_swW_sw, (6.96)

где q_sw и W_sw - определяют согласно пп. 6.6.3 и 6.6.7.

При действии сосредоточенных изгибающих моментов в двух взаимно перпендикулярных плоскостях расчет производят из условия

_{0675S10-02602}

(6.97)

где F, М_х и М_y - согласно п. 6.6.4;

F_{fb , ult} , M_{fbx , ult} и M_{fby , ult} - предельные сосредоточенные сила и изгибающие моменты в направлениях осей X и Y, которые могут быть восприняты сталефибробетоном в расчетном поперечном сечении при их раздельном действии;

F_{sw , ult} , M_{swx , ult} и M_{swy , ult} - предельные сосредоточенные сила и изгибающие моменты в направлениях осей X и Y, которые могут быть восприняты поперечной арматурой при их раздельном действии.

Усилия F_{fb , ult} , M_{fbx , ult} и M_{fby , ult} и F_{sw , ult} определяют согласно пп. 6.6.3 и 6.6.4. Усилия M_{swx , ult} и М_{swy , ult} определяют согласно рекомендациям, приведенным выше, при действии изгибающего момента соответственно в направлении оси X и оси Y.

Значения F_{fb , ult} + F_{sw , ult} , M_{fb , ult} + M_{sw , ult}, M_{fbx , ult} + M_{swx , ult}, M_{fby , ult} + M_{swy , ult} в условиях (6.95) и (6.97) принимают не более 2 F_{fb , ult} , 2 M_{fb , ult}, 2 M_{fbx , ult}, 2 M_{fby , ult} соответственно.

Поперечная арматура должна отвечать конструктивным требованиям, приведенным в разделе 8.

6.6.6 В общем случае значения момента сопротивления расчетного контура сталефибробетона при продавливании W_{fbx ( y )} в направлениях взаимно перпендикулярных осей Х и Y определяют по формуле:

(6.98)

где I_{fbx ( y )} - момент инерции расчетного контура относительно осей Х ₁ и Y ₁, проходящих через его центр тяжести (рис. 6.12);

у (х)_max - максимальное расстояние от расчетного контура до его центра тяжести.

Значение момента инерции I_{fbx ( y )} определяют как сумму моментов инерции I_{fbx ( y ) i} отдельных участков расчетного контура поперечного сечения относительно центральных осей, проходящих через центр тяжести расчетного контура.

Положение центра тяжести расчетного контура относительно выбранной оси определяют по формуле:

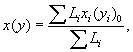(6.99)

где L_i - длина отдельного участка расчетного контура;

x_i (y_i)₀ - расстояние от центров тяжести отдельных участков расчетного контура до выбранных осей.

Для замкнутого прямоугольного контура (рис. 6.12, б, г) с длиной участков L_х и L_y в направлении осей Х и Y центр тяжести расположен в месте пересечения осей симметрии контура.

Значение момента инерции расчетного контура определяют по формуле:

I_{fbx (y)} = I_{fbx (y)1} + I_{fbx (y)2}, (6.100)

где I_{fbx ( y )1,2} - момент инерции участков контура длиной L_x и L_y относительно осей Y ₁ и X ₁, совпадающих с осями Y и X.

Значения I_{fbx ( y )1,2} определяют по формулам (6.101) и (6.102), принимая условно ширину каждого участка контура длиной L_x и L_y, равной единице:

(6.101)

I_{fbx (y)2} = 0,5 L_{x (y)} L ² _{x (y)}. ( 6.102)

Значения W_{fbx ( y )} определяют по формуле:

(6.103)

или W_{fbx ( y )} = L_{x ( y )} L_{y ( x )} + L ² _{x ( y )}/3. (6.104)

Для незамкнутого расчетного контура, состоящего из трех прямолинейных участков длиной L_x и L_y (рис. 6.12, в), например, при расположении площадки передачи нагрузки (колонны) у края плоского элемента (плиты перекрытия), положение центра тяжести расчетного контура в направлении оси X определяют по формуле:

(6.105)

а в направлении оси Y - центр тяжести расположен по оси симметрии расчетного контура.

Значения момента инерции расчетного контура относительно центральных осей Y ₁ и Х ₁ определяют по формуле (6.100).

Значения I_{fbx 1} и I_{fbx 2} определяют по формулам:

_{0675S10-02602}

(6.106)

(6.107)

Значения I_{fby 1} и I_{fby 2} определяют по формулам:

I_{fby 1} = 0,5 L_xL ² _y; (6.108)

I_{fby 2} = L_y ³/12. (6.109)

Значения W_fbx и W_fby определяют по формулам:

и (6.110)

(6.111)

При расчете принимают наименьшие значения моментов сопротивления W_fbx.

Для незамкнутого расчетного контура, состоящего из двух прямолинейных участков длиной L_x и L_y (рис. 6.12, а), например, при расположении площадки передачи нагрузки (колонны) вблизи угла плоского элемента (плиты перекрытия), положение центра тяжести расчетного контура в направлении осей Х и Y определяют по формуле:

_{0675S10-02602}

(6.112)

Значения момента инерции расчетного контура относительно центральных осей Y ₁ и Х ₁ определяют по формулам (6.106) и (6.108).

Значения I_{fbx ( y )1} и I_{fbx ( y )2} определяют по формулам:

_{0675S10-02602}

(6.113)

I_{fbx 2} = L_y (L_x - x_o)²; (6.114)

I_{fby 1} = L_x (L_y - y_o)²; (6.115)

_{0675S10-02602}

(6.116)

Значения W_fbx и W_fby определяют по формулам:

и (6.117)

и (6.118)

При расчете принимают наименьшие значения моментов сопротивления W_fbx и W_fby.

6.6.7 Значения моментов сопротивления поперечной арматуры при продавливании W_{sw , x ( y )} в том случае, когда поперечная арматура расположена равномерно вдоль расчетного контура продавливания в пределах зоны, границы которой отстоят на расстоянии h /2 в каждую сторону от контура продавливания сталефибробетона (рис. 6.14), принимают равными соответствующим значениям W_fbx и W_fby.

При расположении поперечной арматуры в плоском элементе сосредоточенно по осям грузовой площадки, например, по оси колонн (крестообразное расположение поперечной арматуры в перекрытии) моменты сопротивления поперечной арматуры определяют по тем же правилам, что и моменты сопротивления сталефибробетона, принимая соответствующую фактическую длину ограниченного участка расположения поперечной арматуры по расчетному контуру продавливания L_swx и L_swy (рис. 6.12, г).

⇐ Предыдущая567891011121314Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: