Методы обработки результатов экспертизы

При получении оценок в качественных (номинальной или порядковой) шкалах с использованием таких методов высказывания суждений, как разбиение множества, последовательный выбор, последовательное упорядочение, никакой обработки результатов экспертного опроса не требуется. Можно лишь для наглядности представить их в каком-либо графическом виде.

При проведении групповой экспертизы с применением количественных шкал каждому эксперту обычно удобнее пользоваться собственной системой выставления оценок (баллов). Эти системы могут отличаться диапазоном выставляемых оценок (например, от 0 до 5; 0-10; 1-100 и др.). Поэтому для получения общих результатов необходимо индивидуальные оценки экспертов привести к сопоставимому виду, т.е. представить их в единой шкале с фиксированной суммой оценок, равной единице. Такую предварительную процедуру обработки результатов называют нормированием оценок.

Для получения общей групповой оценки можно использовать один из следующих методов:

· среднеарифметическая оценка;

· медиана индивидуальных оценок;

· средневзвешенная оценка;

· правило большинства;

· метод ранга и др.

Пример 3.1. В табл.3.1 приведены результаты групповой экспертизы некоторых объектов. Каждый эксперт пользовался собственной балльной шкалой оценок. Требуется представить результаты в нормированном виде.

Таблица 3.1

Результаты групповой экспертизы

Объекты экспертизы	Оценки экспертов
Э1	Э2	Э3	Э4	Э5	Э6	Э7	Э8
				2,8			9,55
				3,0			9,60
				4,0			9,87
				2,9			9,33
				3,3			9,40
Сумма оценок				16,0			47,75

Подсчитав суммы оценок, выставленных каждым экспертом (последняя строка в табл.3.1), вычислим нормированные оценки. Для этого каждую оценку отнесем к соответствующей сумме оценок. Полученные результаты представлены в табл.3.2.

Обратим внимание на то, что нормированные оценки 7-го эксперта неадекватно отражают его предпочтения, явно прослеживаемые по табл.3.1. Это объясняется по существу неиспользуемым в оценке запасом баллов в выбранной им балльной шкале и малым интервалом варьирования оценок. Неиспользуемый запас баллов – величина неизвестная. Поэтому необходимо путем последовательных приближений установить такое минимальное число, вычитая которое из каждой оценки, проставленной 7-м экспертом, можно было бы получить результаты в нормированном виде, адекватно отражающие его предпочтения.

Таблица 3.2

Промежуточные результаты

Объекты экспертизы	Оценки экспертов в нормированном виде
Э1	Э2	Э3	Э4	Э5	Э6	Э7	Э8
	0,18	0,18	0,19	0,18	0,21	0,19	0,20	0,16
	0,21	0,16	0,21	0,19	0,18	0,19	0,20	0,22
	0,27	0,25	0,25	0,25	0,21	0,25	0,21	0,27
	0,15	0,20	0,18	0,18	0,18	0,19	0,20	0,18
	0,18	0,21	0,17	0,21	0,24	0,19	0,20	0,16

 

Аналогичную ситуацию можно наблюдать и для оценок, выставленных 4-м экспертом. Путем последовательных приближений находим, что неиспользуемый запас баллов у 7-го эксперта равен 8, а у 4-го эксперта – 0,5. С учетом преобразований последовательные ряды оценок

7-го эксперта: 1,55+1,60+1,87+1,33+1,40=7,75;

4-го эксперта: 2,3+2,5+3,5+2,4+2,8=13,5.

В окончательном виде нормированные оценки групповой экспертизы приведены в табл.3.3.

Таблица 3.3

Нормированные оценки групповой экспертизы

Объекты экспертизы	Оценки экспертов в нормированном виде
Э1	Э2	Э3	Э4	Э5	Э6	Э7	Э8
	0,18	0,18	0,19	0,17	0,21	0,19	0,20	0,16
	0,21	0,16	0,21	0,19	0,18	0,19	0,21	0,22
	0,27	0,25	0,25	0,26	0,21	0,25	0,24	0,27
	0,15	0,20	0,18	0,18	0,18	0,19	0,17	0,18
	0,18	0,21	0,17	0,21	0,24	0,19	0,18	0,16

 

Методы определения среднеарифметической оценки и правила большинства не нуждаются в дополнительных пояснениях. Отметим лишь, что правило большинства чаще всего используется при принятии бинарных решений, когда требуется принять решение типа «да/нет», «или/или».

Средневзвешенная по компетентности экспертов оценка определяется, когда известны показатели уровня компетентности каждого из экспертов, участвующих в групповой экспертизе:

,

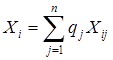где X_i - групповая оценка i -го объекта;

X_ij - индивидуальная оценка i -го объекта j -м экспертом;

q_j - показатель компетентности j -го эксперта.

Методы ранга и медианы поясним на примере обработки результатов групповой экспертизы, информация о которой содержится в табл.3.4 примера 3.2.

Пример 3.2. На основании информации, содержащейся в табл.3.4, вычислим сумму оценок, полученных каждым объектом. После этого найдем отношения каждой суммы оценок объекта к сумме всех суммарных оценок, полученных в результате экспертизы. Это и будет общая групповая оценка, полученная по методу ранга.

В методе медианы из общего количества оценок исключаются 25% самых высоких и 25% самых низких оценок. Таким образом, обработке подлежит только половина всех оценок, которые располагают в упорядоченный ряд. Медиана – это значение параметра, которое делит упорядоченный ряд на две равные по объему группы. При нечетном количестве оставшихся для рассмотрения оценок, т.е. при n = 2 i +1, значение (i +1)-й оценки будет медианным. При четном, т.е. при n = 2 i (в нашем примере n = 4), медианой является средняя арифметическая двух значений, расположенных в середине ряда (в нашем примере это 2-я и 3-я оценки в ряду).

Окончательные результаты представлены в табл.3.4.

Таблица 3.4

Результаты групповой экспертизы

Объекты экспертизы	Оценки экспертов в нормированном виде	Сумма оценок	Групповые оценки
Э1	Э2	Э3	Э4	Э5	Э6	Э7	Э8	по методу ранга	по методу медианы
	0,18	0,18	0,19	0,17	0,21	0,19	0,20	0,16	1,48	0,185	0,185
	0,21	0,16	0,21	0,19	0,18	0,19	0,21	0,22	1,57	0,196	0,200
	0,27	0,25	0,25	0,26	0,21	0,25	0,24	0,27	2,00	0,249	0,250
	0,15	0,20	0,18	0,18	0,18	0,19	0,17	0,18	1,43	0,178	0,180
	0,18	0,21	0,17	0,21	0,24	0,19	0,18	0,16	1,54	0,192	0,185
Сумма оценок	8,02

 

Таким образом, на основании групповых оценок лучшим признан объект 3, далее в порядке убывания значимости объекты 2, 5, 1, 4.

⇐ Предыдущая123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: