 |
Качественный состав экспертной группы
|
|
|
|
На завершающем этапе формирования экспертной группы целесообразно провести тестирование, самооценку, взаимооценку экспертов, анализ их надежности и проверку согласованности мнений.
Тестирование состоит в решении экспертами задач, подобных реальным, с известными (но не экспертам) ответами. На основании результатов тестирования устанавливаются компетентность и профпригодность экспертов.
Самооценка экспертов заключается в ответах на вопросы специально составленной анкеты, в результате чего проверяются профессиональные знания и деловые качества самими же экспертами.
Взаимооценка экспертов друг друга может состоять, например, в составлении каждым экспертом списка группы, которая, по его мнению, компетентна рассматривать решение заданной проблемы.
При наличии сведений о результатах работы эксперта в других экспертных группах критерием его квалификации может быть показатель или степень надежности – отношение числа случаев, когда мнение эксперта совпало с результатами экспертиз, к общему числу экспертиз, в которых он принимал участие.
Проверка согласованности мнений экспертов проводится на контрольных примерах. Вниманию экспертов представляется несколько объектов, которые в зависимости от их качества нужно расставить по шкале порядка, т.е. определить их ранг. Измерение по шкале порядка называется ранжированием. При этом лучшему объекту присваивается высший ранг (число, равное количеству объектов, представленных на экспертизу) и далее по убывающей. Самый худший объект получает ранг, равный единице.
За меру согласованности мнений экспертов принимается так называемый коэффициент конкордации (от лат. concordatum – соглашение):
|
|
|
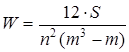 ,
,
где n - количество экспертов; m - количество объектов экспертизы; S - сумма квадратов отклонений суммы рангов каждого объекта экспертизы от среднего арифметического рангов. В зависимости от степени согласованности мнений экспертов коэффициент конкордации W может принимать значения от 0 (при отсутствии согласованности) до 1 (при полной согласованности).
Пример 5.1. Необходимо определить степень согласованности мнений пяти экспертов, участвовавших в групповой экспертизе. Результаты ранжирования ими семи объектов по уровню качества приведены в табл.5.1.
Среднее арифметическое суммы рангов
 .
.
При n =5 и m =7 коэффициент конкордации
 .
.
Коэффициент конкордации близок к единице, следовательно, мнения экспертов хорошо согласованы.
Таблица 5.1
Обработка результатов групповой экспертизы
| Объекты экспертизы | Результаты ранжирования | Сумма рангов | Отклонение суммы рангов от среднего арифметического | Квадрат отклонения от среднего арифметического | ||||
| Э1 | Э2 | Э3 | Э4 | Э5 | ||||
| -5 | ||||||||
| -11 | ||||||||
| -13 | ||||||||
| Среднее арифметическое суммы рангов | ||||||||
| Сумма квадратов отклонений от среднего арифметического рангов |
Задача о лидере»
Одним из наиболее удобных методов индивидуального экспертного оценивания является метод парных сравнений. Психологический механизм любого оценивания предполагает в своей основе парные сравнения. Поэтому эксперту всегда легче высказывать свои суждения в результате попарного сопоставления объектов, кроме того, качество таких суждений оказывается значительно лучшим.
Процедура расстановки приоритетов при попарных сравнениях объектов получила название метода расстановки приоритетов. В своем первоначальном варианте метод расстановки приоритетов известен как метод решения «задачи о лидере», или задачи по определению результатов некоторого спортивного турнира. Определение победителя (лидера) и распределение мест среди других участников турнира производится по сумме набранных игроком или командой очков.
|
|
|
Легко обнаружить аналогию между формальными процедурами проведения какого-либо спортивного турнира и попарного экспертного оценивания объектов, конкурирующих между собой. Результаты такого оценивания эксперт может представить в виде результатов некоторого турнира этих объектов, т.е. в виде системы парных сравнений (турнирной таблицы). Следует только несколько изменить существующий порядок заполнения таких турнирных таблиц.
Дело в том, что в обычном турнире сумма набранных каждым участником очков является показателем его силы, однако этот показатель не учитывает силы соперников (одинаковое количество очков можно набрать, имея разные исходы встреч с соперниками). Решение «задачи о лидере» позволяет учесть эту силу и более точно распределить места между участниками турнира.
Рассмотрим алгоритм решения «задачи о лидере». Для этого представим себе результаты некоторого турнира в виде табл.6.1, в которой за выигрыш игроку или команде начисляется 2 очка, за ничью – 1 очко, за проигрыш – 0 очков. В отличие от обычной турнирной таблицы вместо заштрихованных клеток, означающих, что команда не может встречаться сама с собой, в табл.5.14 проставлен результат, равный единице, что означает отсутствие выигрыша или проигрыша (отсутствие предпочтения) - ничья.
Таблица 6.1
Результаты некоторого турнира в «задаче о лидере» (матрица смежности)
 i
j i
j
| X 1 | X 2 | X 3 | X 4 | Pj (1) | 
|  Pj (2) Pj (2)
| 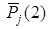
|  Pj (3) Pj (3)
| 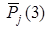
|
| X 1 | 0,375 | 0,397 | 0,385 | |||||||
| X 2 | 0,188 | 0,155 | 0,168 | |||||||
| X 3 | 0,188 | 0,224 | 0,236 | |||||||
| X 4 | 0,250 | 0,224 | 0,212 | |||||||
| Суммы | 1,001 | 1,000 | 1,001 |
Вводится понятие итерированной силы порядка k игрока Xj. Итерированная сила первого порядка Pj (1) находится как сумма очков j -го игрока без учета силы соперников:
|
|
|
 ,
,
где aij - количество очков j -го игрока в каждой встрече; n - количество игроков.
Итерированная сила второго порядка Pj (2) рассчитывается с учетом сил соперников:
 .
.
Итерированные силы последующих порядков вычисляются аналогично:
 и т.д.
и т.д.
С каждой последующей итерацией значения Pj (k) все время уточняются.
Через 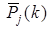 в табл.6.1 обозначены итерированные силы порядка k в норми-рованном виде.
в табл.6.1 обозначены итерированные силы порядка k в норми-рованном виде.
Поясним вычисления, результаты которых занесены в табл.6.1.

 и т.д.
и т.д.

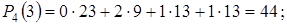
 и т.д.
и т.д.
Интересно проследить по табл.6.1, как изменяется распределение мест среди участников турнира по мере вычисления итерированных сил каждого следующего порядка. Так, после обычного подведения итогов – вычисления суммы очков - места участников могут быть распределены следующим образом: 1-е место – X 1, 2-е место - X 4, 3-е место - X 2, 4-е место – X 3, т.к. X 2 выиграл у X 3 в личной встрече.
После вычисления итерированных сил второго порядка, которые учитывают силы соперников, ситуация в распределении мест изменяется: 1-е место по-прежнему за X 1, 2-е место - X 4, а на 3-е место нужно поставить X 3, т.к.  .
.
Ситуация окончательно уточняется после вычисления итерированных сил третьего порядка: 1-е место – X 1, 2-е место - X 3, 3-е место - X 4, 4-е место – X 2.
7. Метод расстановки приоритетов [1]
Алгоритм решения «задачи о лидере» - это один из простейших вариантов реализации метода расстановки приоритетов; его можно с успехом применять в случаях:
· определения лучшего объекта из заданной совокупности по заранее сформулированному признаку;
· упорядочения объектов по степени выраженности заданного признака.
При решении перечисленных задач требуется только проранжировать объекты в порядке предпочтения по шкале порядка. Если же необходимо найти количественную меру предпочтения, как, например, при вычислении весовых коэффициентов, то алгоритм решения «задачи о лидере» нуждается в некотором усовершенствовании.
Дело в том, что при решении «задачи о лидере» мы основывались на произвольно выбранной системе оценок (выигрыш – 2 очка, ничья – 1 очко, проигрыш – 0 очков). Поэтому получаемые в конечном итоге численные значения приоритетов (значения итерированных сил 1-го, 2-го и т.д. порядков) нельзя интерпретировать как количественную меру степени превосходства одного объекта над другим. Для подобной интерпретации необходимо согласовать систему оценок с мерой превосходства (или предпочтения) одного объекта (или признака) над другим. Такое согласование достигается путем последовательных приближений (или методом итераций).
|
|
|
В усовершенствованном виде алгоритм метода расстановки приоритетов (МРП) сводится к следующему.
1. Устанавливается система оценок, зависящая от некоторого параметра y, уточняемого в процессе решения задачи:

где  любое рациональное число в заданном интервале.
любое рациональное число в заданном интервале.
2. На основе анализа имеющейся информации или с помощью экспертной оценки задаются пределы изменения степени выраженности данного признака в оцениваемых объектах, которые фиксируются в виде отношения крайних членов ранжированного ряда:
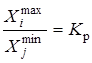 ,
,
где 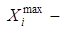 объект с максимальной оценкой критерия (признака);
объект с максимальной оценкой критерия (признака);
 объект с минимальной оценкой критерия (признака);
объект с минимальной оценкой критерия (признака);
K p - расчетный коэффициент отношения.
3. По найденному отношению K p определяют параметр y, который в первом приближении устанавливают равным
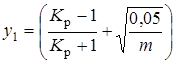 ,
,
где m - число оцениваемых объектов.
4. С выбранной системой оценок методом расстановки приоритетов решается задача (заполняется матрица смежности). Получаемые в результате величины итерированных сил k -го порядка (при k = 1, 2, 3, …) являются оценками объектов (или весовыми коэффициентами признаков) в первом приближении. Увеличение порядка итерированных сил способствует уточнению результатов первого приближения, однако можно ограничиться вычислениями на этом этапе до k = 3.
5. Рассчитывается фактический коэффициент отношения оценок крайних членов ранжированного ряда:
 .
.
Если  существенно отличается от единицы, то производится следующее приближение
существенно отличается от единицы, то производится следующее приближение  , устанавливается новая система оценок и решение повторяется, начиная с п. 4. Затем в п. 5 вычисляется новое значение фактического коэффициента, которое сравнивается с предыдущим, и т.д. При согласованности коэффициентов задача считается решенной.
, устанавливается новая система оценок и решение повторяется, начиная с п. 4. Затем в п. 5 вычисляется новое значение фактического коэффициента, которое сравнивается с предыдущим, и т.д. При согласованности коэффициентов задача считается решенной.
Достоинством метода расстановки приоритетов является тот факт, что его практическое применение не требует строгой транзитивности – логичности предпочтений (если a лучше b, а b лучше c, то и a лучше c). Нетранзитивность (нарушение логичности) системы попарных сравнений может встречаться по разным причинам: большое количество объектов, неодинаковый порог различения и др.
При отсутствии требования транзитивности системы сравнений эксперт производит сопоставление объектов независимо от результатов других сопоставлений и одна-две допущенные ошибки практически не повлияют на результаты расчета значений приоритетов объектов.
|
|
|
Пример 7.1. Важным этапом изучения курса «Управление качеством» является завершающая стадия – оценка результатов обучения. Совокупная (комплексная) оценка за учебный курс может складываться из следующих показателей:
1) посещаемости занятий;
2) активности обучения – проявления заинтересованности (выяснение возникающих вопросов) в ходе всего учебного процесса, участия в обсуждении конкретных ситуаций (обоснованность, доказательность и аргументированность выдвигаемых предложений) на практических занятиях, участия в выполнении учебных научно-исследо-вательских работ и др.;
3) результатов аттестаций – промежуточных контрольных мероприятий;
4) оценки выполнения домашних заданий (контрольных, курсовых работ и проектов);
5) оценки знаний на экзамене.
Определим значимость (весовые коэффициенты) каждого из перечисленных показателей качества обучения в совокупной (комплексной) оценке, выставляемой студенту на экзамене по курсу «Управление качеством». Для этого воспользуемся методом расстановки приоритетов.
С точки зрения авторов, наиболее значимым показателем качества обучения следует считать 2-й показатель – активность обучения, наименее значимым из перечисленных – результаты аттестаций. Зададимся отношением этих крайних членов пока еще не ранжированного ряда:
 .
.
Тогда параметр y в первом приближении выбирается равным
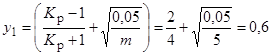 ;
;
система оценок:

Составляем матрицу смежности.
| Показатели | Pj (1) | 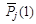
| Pj (2) | 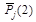
| Pj (3) | 
| |||||||||||||
| 1. Посещаемость | 0,4 | 1,6 | 0,4 | 4,4 | 0,176 | 18,4 | 0,165 | 80,48 | 0,165 | ||||||||||
| 2. Активность | 1,6 | 1,6 | 1,6 | 1,6 | 7,4 | 0,296 | 35,56 | 0,319 | 156,78 | 0,321 | |||||||||
| 3. Аттестация | 0,4 | 0,4 | 0,4 | 0,4 | 2,6 | 0,104 | 11,56 | 0,104 | 51,46 | 0,105 | |||||||||
| 4. Дом. задание | 0,4 | 1,6 | 0,4 | 4,4 | 0,176 | 18,4 | 0,165 | 80,48 | 0,165 | ||||||||||
| 5. Экзамен | 1,6 | 0,4 | 1,6 | 1,6 | 6,2 | 0,248 | 27,4 | 0,246 | 119,00 | 0,244 | |||||||||
| Сумма | 25,0 | 1,000 | 111,32 | 0,999 | 488,20 | 1,000 | |||||||||||||
Фактический коэффициент отношения оценок крайних членов ранжированного ряда:
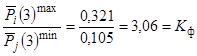 .
.
Если считать, что отношение  существенно отличается от единицы, то необходимо произвести еще одно приближение
существенно отличается от единицы, то необходимо произвести еще одно приближение  , установить новую систему оценок и решение повторить. Однако будем считать достигнутую точ- ность в первом приближении достаточной. Тогда значения итерированных сил
, установить новую систему оценок и решение повторить. Однако будем считать достигнутую точ- ность в первом приближении достаточной. Тогда значения итерированных сил  являются коэффициентами значимости показателей качества обучения. Так, например, если студент по первым четырем показателям имеет оценки «удовлетворительно» (3), а на заключительном экзамене его знания оценены с оценкой «хорошо», то определяющей (комплексной) оценкой по дисциплине следует считать:
являются коэффициентами значимости показателей качества обучения. Так, например, если студент по первым четырем показателям имеет оценки «удовлетворительно» (3), а на заключительном экзамене его знания оценены с оценкой «хорошо», то определяющей (комплексной) оценкой по дисциплине следует считать:
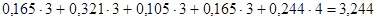 - «удовлетворительно».
- «удовлетворительно».
Резюме
1. Для управления качеством продукции необходимо уметь определять уровень качества. Уровень качества продукции – это относительная характеристика качества, основанная на сравнении значений показателей качества оцениваемой продукции с соответствующими показателями базового образца.
2. Область деятельности, связанная с определением, измерением и вообще с количественной оценкой качества продукции, называется квалиметрией.
3. Показатель качества – это количественная характеристика одного или нескольких свойств продукции, составляющих ее качество, рассматриваемая применительно к определенным условиям ее создания, эксплуатации или потребления.
4. Показатели качества продукции можно классифицировать по характеризуемым свойствам (назначению, надежности, технологичности и др.), по количеству характеризуемых свойств, по способу выражения единиц измерения, по применению для оценки, по стадии определения и др.
5. Промышленная продукция по характеру реализации ее свойств при использовании разделяется на два класса:
· продукция, расходуемая при использовании (природное сырье и топливо, материалы и продукты, расходуемые изделия);
· продукция, расходующаясвой ресурс (неремонтируемые изделия, ремонтируемые изделия).
6. Услуги можно классифицировать по четырем признакам:
· область распространения (среди населения, в сфере производства);
· назначение (материальные, нематериальные);
· характер потребления (индивидуальные, коллективные);
· условия предоставления (платные, льготные, бесплатные).
7. Основные группы показателей качества услуг:
· надежность;
· компетентность и ответственность;
· достоверность, полнота и доступность информации;
· культура обслуживания, этика общения.
· санитарно-гигиеническое состояние салонов и производственных помещений;
· комплексность, ассортимент и совместимость услуг;
· безопасность и экологичность при обслуживании.
8. Показатели качества продукции могут быть абсолютными и относительными, единичными и комплексными. Абсолютные значения всегда имеют размерность, относительные – всегда безразмерные. Относительные значения единичных показателей качества определяют по отношению к соответствующим показателям базового образца. Единичный показатель качества характеризует одно простое свойство продукции; комплексный показатель характеризует совместно несколько простых свойств или одно сложное свойство продукции.
9. В квалиметрии применяют способ образования комплексных показателей по принципу среднего взвешенного. В зависимости от степени однородности величин слагаемых применяют либо среднее взвешенное арифметическое, либо среднее взвешенное гармоническое, либо среднее взвешенное геометрическое.
10. Комплексный показатель качества должен объективно соединять и представлять комплекс простых и сложных свойств продукции. Поэтому он должен отвечать требованиям репрезентативности, монотонности, критичности, нормированности и сравниваемости по отношению к включаемой в него информации.
11. Для определения показателей качества продукции существуют измерительный, регистрационный, расчетный, органолептический, экспертный и социологический методы. Основным из них является измерительный метод в силу наибольшей объективности получаемой информации. Поэтому он должен применяться всегда, когда это возможно и экономически оправдано.
12. Для оценки уровня качества продукции применяют дифференциальный, комплексный или смешанный методы. Дифференциальный метод предполагает оценку по нескольким отдельным показателям. Комплексный метод предусматривает использование комплексного (обобщенного) показателя качества, выраженного одним числом. Для оценки уровня качества сложной продукции, имеющей широкую номенклатуру показателей качества, используют смешанный метод.
13. Когда невозможно применение других, более объективных методов измерений используют методы экспертного оценивания. Процедура экспертного оценивания предполагает наличие и применение заранее предусмотренных шкалы измерения информации, метода высказывания суждений экспертом и метода обработки результатов экспертизы.
14. Существуют номинальные, порядковые, интервальные шкалы и шкала отношений. Номинальные и порядковые шкалы – это чисто качественные шкалы, а шкалы интервалов и отношений – количественные шкалы. Выбор той или иной шкалы для измерений обусловлен спецификой решаемой задачи, уровнем компетентности экспертов и другими факторами.
15. При получении индивидуальных экспертных оценок различают методы разбиения множества, последовательного выбора и последовательного упорядочения, методы парных сравнений, балльной оценки, непосредственной количественной оценки и метод деления пополам.
16. Методы групповой экспертной оценки, такие как заочный опрос, интервью, дискуссии, метод Дельфы, позволяют повысить уровень объективности индивидуальных оценок благодаря использованию суждений большего числа экспертов и применению определенных процедур приведения индивидуальных мнений к единому, групповому.
17. В качестве методов обработки результатов экспертизы для получения общей групповой оценки можно использовать среднеарифметическую оценку, средневзвешенную по компетентности экспертов оценку, медиану индивидуальных оценок, правило большинства, метод ранга и др.
18. На качество результатов экспертизы оказывают влияние количественный и качественный состав группы. Поэтому на завершающем этапе формирования экспертной группы целесообразно провести тестирование, самооценку, взаимооценку экспертов, анализ их надежности и проверку согласованности мнений.
19. Одним из наиболее удобных методов индивидуального экспертного оценивания является метод расстановки приоритетов в парных сравнениях объектов (или признаков) между собой. Алгоритм этого метода очень похож на обычную процедуру подведения итогов какого-либо спортивного турнира, однако отличается от нее тем, что позволяет учитывать ите-
рированные силы соперников (или объектов, признаков в экспертном оценивании). Метод легко реализуется, когда необходимо проранжировать объекты (или признаки) в порядке предпочтения по шкале порядка.
20. Метод расстановки приоритетов дает количественную оценку степени превосходства одного объекта (или признака) над другим, если согласовать принятую систему предпочтений с количественной мерой. Согласование достигается путем итераций. Такой вариант метода применим для определения величин весовых коэффициентов при показателях качества продукции.
[2] Гоголь Н.В. Собрание сочинений в восьми томах. Т.5.- М.: Правда, 1984. - С.5.
[3] Предложен в начале 50-х гг. ХХ века американскими учеными Т.Дж.Гордоном и О.Хелмером для решения военных проблем. Название происходит от древнегреческого города Дельфы, где, по преданию, при храме Апполона с IX в. до н.э. по IV в. н.э. существовал совет мудрецов («дельфийский оракул»), славившийся своими предсказаниями.
|
|
|


