 |
Принцип воспитывающего обучения
|
|
|
|
Всякое обучение должно быть воспитывающим, т. е. наряду с определенными обучающими функциями должны осуществляться и воспитательные функции. Отсюда, однако, не следует, что все воспитание сводится к обучению. Наоборот, по-видимому, правильнее будет считать, что обучение является составной частью системы воспитания.
Воспитание в процессе обучения вообще, и математике в частности, имеет своей основной целью формирование у школьника мировоззрения и морали. Как решается эта задача при начальном обучении математике? На этом этапе обучения необходимо прежде всего показать, что всем изучаемым понятиям и фактам соответствуют реальные объекты, свойства и отношения между ними. Именно в начальном обучении иллюстрируется на многочисленных примерах известное утверждение Ф. Энгельса о том, что натуральные числа и геометрические фигуры взяты из реального мира, а не возникли из чистого мышления. Мы неоднократно обращаемся к реальным прообразам количественных отношений и пространственных форм. т. е. начинаем по существу формирование правильных представлений о предмете математики, о том, что математика, как и другие науки, изучает окружающий нас реальный мир.
Мораль - это совокупность норм и правил поведения людей во всех сферах общественной жизни. В математике существует много правил, которые нужно строго выполнять. Воспитание строгости соблюдения разного рода математических правил (алгоритмов) способствует и воспитанию правил поведения в обществе, соблюдению норм, регулирующих отношения между людьми.
На уроках математики учитель имеет большие возможности для воспитания у учащихся честности, трудолюбия, стремления к преодолению трудностей и т. д. Важнейшим средством воспитания этих качеств являются арифметические задачи, текст которых выполняет воспитательную функцию. Воспитывающий характер обучения в значительной мере зависит также от методов преподавания.
|
|
|
Научность в обучении
В соответствии с этим принципом учебный материал должен излагаться в последовательности, сохраняющей связи между понятиями, темами, разделами в рамках отдельного предмета, а также межпредметные связи. Таким образом, принцип научности в обучении включает систематичность и последовательность (иногда в педагогической литературе этот принцип называют принципом научности, систематичности и последовательности в обучении).
Научность в обучении математике не означает, что в учебную программу включается система математических знаний в том виде, в котором она существует в науке математике. Применительно к начальному обучению математике принцип научности следует понимать как отражение в нем определенных математических идей, позволяющее осуществить их раннюю пропедевтику. Такими фундаментальными математическими идеями являются идеи числа, функциональной зависимости, геометрической фигуры, измерения величин, алгоритма.
В начальных классах формируется представление о натуральном ряде как об упорядоченном, дискретном множестве с первым и без последнего элемента. Такие используемые в практике обучения выражения, как "соседние числа", "сосед справа", "сосед слева", соответствуют отношениям, рассматриваемым в науке математике, "непосредственно следует за", "непосредственно предшествует".
Свойства натурального ряда - "для каждого числа имеется единственный сосед справа", "для каждого числа, кроме 1, имеется единственный сосед слева", "сосед справа получается прибавлением 1", "сосед слева получается вычитанием 1" - отражают идеи порядковой теории натурального ряда и значения функции прибавления 1 для формирования этого ряда.
|
|
|
В первом классе смысл операции сложения раскрывается через объединение множеств конкретных предметов. При этом неявно используется известное положение количественной теории натуральных чисел:

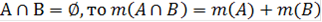
"Открываемая" младшими школьниками зависимость между результатами и компонентами арифметических операций служит пропедевтикой идеи функциональной зависимости.
В начальных классах важно сформировать представление о замкнутости множества натуральных чисел относительно отдельных операций: для любых двух натуральных чисел можно найти их сумму, их произведение, но не для любых двух натуральных чисел можно найти натуральное число, равное их разности или их частному.
Ознакомление учащихся с процедурой измерения отрезков служит подготовкой к усвоению ими в дальнейшем более общих вопросов теории измерения величин.
Сознательность усвоения
Сознательность усвоения понимается как такое овладение учащимися знаниями, которое включает глубокое понимание усвоенного и умение применять его в новых конкретных ситуациях.
Трудности, связанные с реализацией принципа сознательности, обусловлены отчасти тем, что механизм понимания недостаточно изучен. Однако можно все же утверждать, что если ученик понял, какой - то материал, то он должен уметь отвечать на такие вопросы, решать какие - то задачи (важно правильно подобрать соответствующие вопросы и задачи). Если же ученик не справляется с этими вопросами и задачами, значит, он не понял данный материал.
В процессе обучения учитель должен постоянно получать информацию о качестве усвоения учащимися изучаемого материала. Это особенно важно при начальном обучении математике, так как непонимание последующего материала. Чтобы выяснить, заучен материал или же понят, нужна педагогически целесообразная система вопросов и задач. Считают, что вопрос "педагогически целесообразно" поставлен, если он вызывает активную мыслительную деятельность учащегося и не допускает ответа заученными словами из учебника.
Сознательное усвоение знаний исключает догматическое преподавание, результатом которого являются "формальные знания". Формализм чаще всего встречается при обучении математики, в частности широким использованием в ней искусственного символического языка. Учащиеся иногда ориентируются на запоминание внешнего символического выражения содержательного математического факта. Формальные знания бесполезны, так как их невозможно применять на практике. Так, ученик может знать таблицы сложения и умножения чисел, но не понимать, в каких задачах применяются действия сложения и умножения чисел от конкретных, реальных интерпретаций этих записей в процессе их изучения.
|
|
|
Активность учащихся
Сознательность усвоения предполагает активность учащихся в процессе обучения. Без активной мыслительной деятельности не может быть достигнуто сознательного усвоения знаний. Различают активность в широком и узком смысле. Активность в широком смысле при обучении математике существенно не отличается от активности учащихся в процессе обучения их другим предметам, т. е. она не затрагивает специфику учебного предмета. Активность же в узком смысле можно понимать как проявление специфической мыслительной деятельности, характерной для ученого - математика и называемой потому "математической" деятельностью.
На первый взгляд сама постановка проблемы обучения математической деятельности может показаться неправомерной. Действительно, способен ли ученик младших классов школы к математической деятельности? Очевидно, что к математической деятельности на высоком логическом уровне не способен ни ученик 3-го, ни ученик 10-го класса. Но к какой - то математической деятельности, адекватной уровню мышления, способен и первоклассник. Все зависит от того, что мы понимаем под "математической деятельностью".
Когда первоклассник (или дошкольник) образует пары элементов из двух множеств и приходит к выводу, что в одном множестве больше предметов, чем в другом, он уже осуществляет некоторую, хотя и весьма примитивную, математическую деятельность. Усваивая понятие арифметической операции, ученик переходит от действия над множествами конкретных предметов к операциям над соответствующими числами.(числами элементов этих множеств), отвлекаясь при этом от природы предметов. Это тоже математическая деятельность, но на более высоком уровне. Открывая законы действий над числами, отвлекаясь при этом от конкретных чисел, заменяя их буквами (или пустыми окошками различной формы), он осуществляет математическую деятельность на еще более высоком уровне.
|
|
|
Обучение математике может и должно строиться так, чтобы начиная с первого класса ученик последовательно переходил от одного уровня математической деятельности к другому, более высокому.
Известный математик-педагог Д. Пойа так формулирует принцип активного учения: лучший способ изучить что-нибудь - это открыть самому. Хотя ученик третьего класса "открывает", то, что уже давно открыто, он мыслит при этом как первооткрыватель. Важная задача методики преподавания - стимулировать открытия учащихся.
Наглядность обучения
Наглядное обучение, по словам К. Д. Ушинского, - такое обучение, которое строится не на отвлеченных представлениях и словах, а на конкретных образах, непосредственно воспринятых ребенком. Наглядность очень важна при начальном обучении математике в связи с особенностью конкретно-образного мышления младших школьников. В средних и старших классах широко используется символическая деятельность (чертежи, графики, графы, схемы, таблицы и др.). При начальном же обучении математике применяются все виды наглядности: натуральная, символическая и особенно изобразительная. Например, приступая к изучению числа и цифры 5, показывают различные картинки, на каждой из которых изображено множество каких - либо предметов, причем общим для всех этих множеств является лишь то, что каждое состоит из пяти элементов (карандашей, птиц, рыб, мальчиков, автомашин и т. д.). Широкое использование изобразительной наглядности связано с тем, что на начальном этапе обучения математике математические понятия абстрагируются от их реальных прообразов. Используется также символическая наглядность, сначала в сочетании с изобразительной. Так, например, желая показать, что девочек на одной картинке столько же, сколько мячиков, изображенных на другой картинке, проводят стрелки от каждой девочки к одному из мячиков так, чтобы никакие две стрелки не оканчивались у одного мячика. Конечно, эти стрелки можно истолковать, как обозначения выбора мячика девочкой. При формировании представлений об отношениях "меньше", "больше" рассматриваются случаи, когда всем девочкам не хватает мячиков ("Леночка плачет, ей не достался мячик") и когда остаются лишние мячики. От этой изобразительно-символической наглядности до чисто символической наглядности один шаг. Можно и девочек и мячик обозначать какими-нибудь фигурами, например треугольниками, кружочками или просто точками.
|
|
|
Любое средство символической наглядности представляет собой условную знаковою систему, с помощью которой изучаемые свойства предметов, явлений, процессов отделяются от прочих свойств. Таким образом, символическая наглядность является по существу своеобразным языком. Так, например, чтобы стрелки, о которых шла речь выше, стали понятными, необходимо разъяснить, что они обозначают. То же можно сказать и о записях 5 +3=8, 5 х 3=15 и т. д. Каждая из них становится наглядной лишь после того, как проиллюстрируют с помщью какой-нибудь реальной ситуации, которую она описывает, т. е. после того, как разъяснена ее семантика (выраженный этой записью смысл).
Часто символическая запись, например 5 х 3=15, может иллюстрироваться с помощью геометрической модели, например прямоугольника, изображенного на бумаге, длина которого 5, а ширина 3 клеточки. В таком случае легко определить произведение - число клеточек, содержащихся в изображенном прямоугольнике, легко "доказать" свойство коммутативности (переместительности) умножения, сосчитав число клеточек по рядам и столбцам (слово "доказать" взято в кавычки, так как это предматематическое доказательство на частном случае, модели).
Важную роль играет наглядность при формировании математических понятий. Обычно различают две ступени этого процесса: чувственную, состоящую в формировании ощущений, восприятия и представления, и логическую, заключающуюся в переходе от представления к понятию с помощью обобщения и абстрагирования.
Прочность знаний
Сохранение у учащихся в течение длительного времени систематизированных знаний, умений и навыков возможно лишь при осознанном усвоении знаний. Сознательность усвоения обеспечивается активной мыслительной деятельностью, поэтому необходимым условием прочности знаний является приобретение их активным способом. Однако наряду с сознательностью и активностью необходима также соответствующая организация обучения, учитывающая особенности механизма запоминания. Существуют следующие общедидактические положения: а) запоминание находится в прямой зависимости от повторения; б) память имеет избирательный характер - запоминается преимущественно то, что для нас существенно, интересно; в) материал запоминается лучше, когда раскрываются возможности применения его на практике; г) запоминанию способствует разделение изучаемого материала на небольшие порции по смысловому содержанию с выделением опорных пунктов в форме заголовков, вопросов, математических соотношений; д) эмоционально окрашенный материал запоминается лучше.
Вопрос о том, что должен запомнить ученик из изучаемого материала, гораздо сложнее, чем может показаться на первый взгляд. Совершенно очевидно, что запомнить все невозможно да и не нужно, если имеется в виду весь школьный курс математики. В курсе же математики начальных классов почти все подлежит запоминанию: таблицы сложения и умножения однозначных чисел, алгоритмы выполнения четырех арифметических действий над многозначными числами и т. д.
Повторение ранее изученного материала перед изучением новой темы является одним из важнейших видов повторения при обучении математике вообще и в начальных классах в частности. Оно способствует лучшему запоминанию как старого, так и нового материала.
Индивидуальный подход в обучении
При обучении необходимо учитывать особенности мышления каждого ученика, свойства его памяти, отдельных анализаторов (зрение, слух) и т. д. Даже у учащихся одного возраста они различны, поэтому один и тот же материал одни учащиеся усваивают быстрее, а другие медленнее. Все это и обуславливает необходимость индивидуального подхода в обучении.
Если бы можно было как-то "измерить" скорость усвоения математического материала различными учащимися, то разброс был бы намного больше, чем по другим предметам. Ориентирование на "среднего" ученика приводит к отрицательным последствиям. Слабые учащиеся, находящиеся ниже уровня "среднего", становятся неуспевающими, а сильные начинают скучать на уроках и теряют интерес к предмету. Поэтому в условиях классно-урочной системы, когда в классе одновременно обучается 30-40 человек, необходимо осуществлять принцип индивидуального подхода, использовать различные приемы, учитывающие особенности усвоения материала различными учащимися (дифференцированные задания, опережающие, выравнивающие занятия, дополнительные индивидуальные занятия, кружковые занятия и т. д.). Одно из возможных решений проблемы индивидуального подхода связано с использованием в обучении персональных компьютеров.
Метод как многомерное явление
Поиск ответа на традиционный дидактический вопрос - как учить - выводит нас на категорию методов обучения. Без методов невозможно достичь поставленной цели, реализовать намеченное содержание, наполнить обучение познавательной деятельностью. Метод - сердцевина учебного процесса, связывающее звено между запроектированной целью и конечным результатом. Его роль в системе "цели - содержание - методы - формы - средства обучения" является определяющей.
Метод обучения (от греч. metodos - буквально: путь к чему-либо) - это упорядоченная деятельность педагога и учащихся, направленная на достижение заданной цели обучения. Под методами обучения (дидактическими методами) часто понимают совокупность путей, способов достижения целей, решение задач образования. В педагогической литературе понятие метода иногда относят только к деятельности педагога или к деятельности учащихся. В первом случае уместно говорить о методах преподавания. А во втором - о методах учения. Если же речь идет о совместной работе учителя и учащихся, то здесь, несомненно, проявляются методы обучения. В структуре методов обучения выделяются приемы. Прием - это элемент метода, его составная часть, разовое действие, отдельный шаг в реализации метода или модификация метода в том случае, когда метод небольшой по или простой по структуре.
Метод обучения - сложное, многомерное, многокачественное образование. Если бы нам удалось построить его пространственную модель, то мы бы увидели причудливый кристалл, сверкающий множеством граней и постоянно меняющий свою окраску. Именно такую конфигурацию предлагают и высвечивают на экранах современные ЭВМ при попытке наглядного моделирования метода. В методе обучения находят отражение объективные закономерности, цели, содержание, принципы, формы обучения. Диалектика связи метода с другими категориями дидактики взаимообратная: будучи производным от целей, содержания, форм обучения, методы в то же время оказывают обратное и очень сильное влияние на становление и развитие этих категорий. Ни цели, ни содержание, ни формы работы не могут быть введены без учета возможностей их практической реализации, именно такую возможность обеспечивают методы. Они же задают темп развития дидактической системы - обучение прогрессирует настолько быстро, насколько позволяют ему двигаться вперед применяемые методы.
В структуре методов обучения выделяются прежде всего объективная и субъективная части. Объективная часть метода обусловлена теми постоянными, незыблемыми положениями, которые обязательно присутствуют в любом методе, независимо от его использования различными педагогами. В ней отражаются общие для всех дидактические положения, требования законов и закономерностей, принципов и правил, а также постоянные компоненты целей, содержания, форм учебной деятельности. Субъективная часть метода обусловлена личностью педагога, особенностями учащихся, конкретными условиями. Очень сложным и не вполне еще разрешенным является вопрос о соотношении объективного и субъективного в методе. Диапазон мнений по данному вопросу очень широк: от признания метода чисто объективным образованием до полного отрицания объективных начал и признания метода личным, а поэтому неповторимым произведением педагога. Истина, как всегда, находится между крайностями. Именно наличие в методе постоянной, общей для всех объективной части позволяет разрабатывать теорию методов, рекомендовать практике пути, являющиеся наилучшими в большинстве случаев, а также успешно решать проблемы логического выбора, оптимизации методов. Справедливо и то, что в области методов больше всего проявляется собственное творчество, индивидуальное мастерство педагогов, а поэтому методы обучения всегда были и всегда останутся сферой высокого педагогического искусства.
Методы обучения математике
Общие и специальные методы
В дидактической литературе встречаются различные определения понятия "метод обучения". Будем исходить из достаточно широко распространенного представления о методах обучения как об упорядоченных способах взаимосвязанной деятельности учителя и учащихся, направленных на достижение целей обучения как средства образования и воспитания. Описание каждого метода обучения должно раскрывать: 1) обучающую деятельность учителя; 2) содержание учебной (познавательной) деятельности ученика; 3) связь между ними, т. е. способ, с помощью которого учитель управляет познавательной деятельностью учащихся.
В дидактике рассматриваются, однако, лишь общие методы обучения, т. е. методы не учитывающие специфики отдельных предметов. Исследование возможностей конкретной реализации общих методов в начальном обучении математике путем их модификации, адаптации с учетом специфики математики и мыслительной деятельности учащихся начальных классов является предметом методики начального обучения математике. Используются также специальные методы обучения, отражающие особенности математического познания.
Специальные методы обучения, и прежде всего метод моделирования (построения математических моделей), в наибольшей степени влияют на формирование и развитие математического стиля мышления.
|
|
|


