 |
Решение Шварцшильда как базовая метрика
|
|
|
|
Итак, решение Шварцшильда имеет вид
, (2.2.1)
где 
– координаты кривизны, а
, 
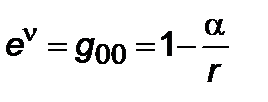. (2.2.2)
Здесь 
– гравитационный радиус, равный
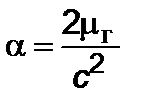, (2.2.3)
– гравитационная постоянная тела. Хотя поле Шварцшильда не вполне отражает поле реальных небесных тел, оно позволяет учесть релятивистские поправки, особенно важные при движении ракеты вблизи мощных гравитационных полей (“черных дыр”).
В работе [8], используя предельный переход Диксона и Фока (стремление объема материи к сосредоточенной точке), получаем из (2.1.1) уравнения движения в виде
(2.2.4)
.
Здесь, как отмечалось выше, 
определяют свойства риманового пространства, а именно связность неплоского пространства, 
– компоненты негравитационных сил (сил трения, электромагнитных сил), 
– относительная масса выхлопа ракеты,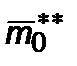 
– относительная масса внешних частиц. По определению, 4– мерная скорость есть
, (2.2.5)
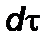– интервал времени по часам в ракете, 
– хронометрически инвариантная скорость; между скоростью 
и скоростью 
существует связь
. (2.2.6)
Аналогично определяются скорость частиц выхлопа 
и скорости набегающих на ракету внешних частиц 
.
Обозначая через 
компоненту реактивного ускорения 
, запишем (2.2.4) в виде (учитывая лишь реактивные силы)
, 
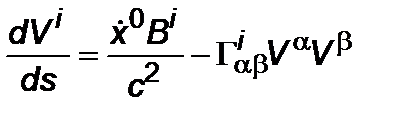, (2.2.7)
. (2.2.8)
При отсутствии внешних полей имеем просто
. (2.2.9)
Рассмотрим одномерное движение ракеты в бессиловом поле. Тогда, по определению, имеем для случая лишь отбрасывания частиц выражение для реактивного ускорения
, 
, (2.2.10)
где 
– скорость выхлопа. Из (2.2.9) имеем
, (2.2.11)
но 
. В итоге получим
. (2.2.12)
В случае постоянной скорости 
, равной
, (2.2.13)
где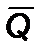 
– теплопроводная способность топлива, интегрирование (2.2.12) дает решение Аккерета
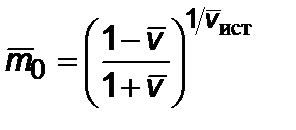, (2.2.14)
являющееся релятивистским аналогом формулы Циолковского
|
|
|
. (2.2.15)
Формула (2.2.13) определяет адиабатический процесс на срезе сопла. В случае термоядерного синтеза, в процессе которого возможен процесс воспроизводства гелия-3 (He3) – основного горючего термояда, не исключены рост теплотворной способности горючего и рост скорости истечения. Аналогичные особенности могут возникнуть в ракете при отборе (использовании) внешней среды (водорода), а также при иных физических процессах в ракете (например, аннигиляции). Поэтому можно представить скорость истечения в виде зависимости от скорости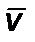 
, (2.2.16)
где коэффициенты 
и 
определяются из начальных и конечных условий; например, выражение 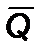определится из (2.2.13), когда начальный процесс – адиабатичный и 
; коэффициент 
определится из условия максимальной возможной скорости истечения, характерного для термояда 
и 
для аннигиляции. При этом следует учитывать условия реактивного коэффициента полезного действия 
, равного отношению разности мощности реактивной тяги и мощности потока выхлопа к полной мощности
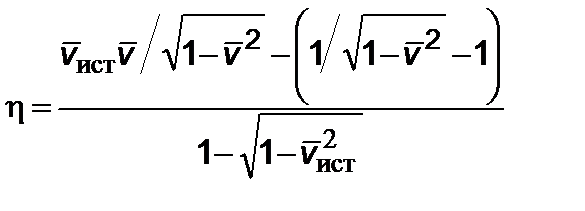. (2.2.17)
Максимум (2.2.17) имеет при условии 
. Итак, из (2.2.12) имеем
. (2.2.18)
Данное выражение является обобщением решения Аккерета на случай переменной скорости истечения. Приближенно, пренебрегая выражением под корнем, получим решение
. (2.2.19)
Уравнения релятивистской баллистики
Если спроектировать в евклидовой плоскости уравнения движения (2.2.7) и энергии ракеты (2.2.8), то получим
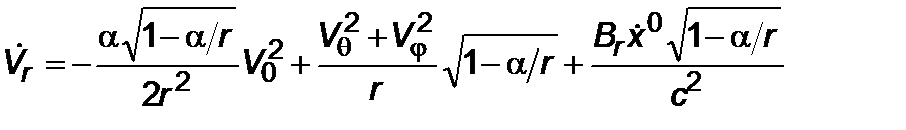, (2.3.1)
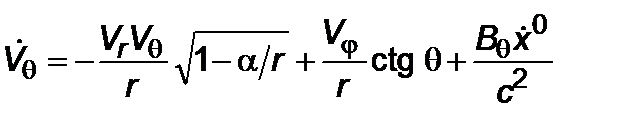, (2.3.2)
, (2.3.3)
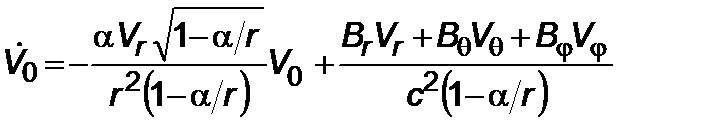. (2.3.4)
Здесь 
, 
, 
.
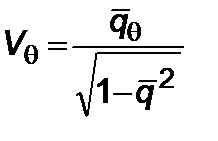Проекции записаны вдоль координат кривизн 
. Для плоского движения, учитывая соотношения
, 
, (2.3.5)
где 
, имеем
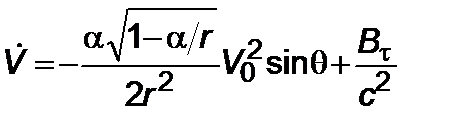, (2.3.6)
, (2.3.7)
, (2.3.8)
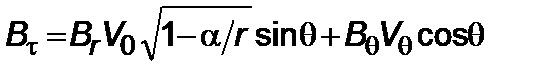, (2.3.9)
(2.3.10)
или
, 
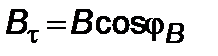, (2.3.11)
, 
– угол между касательной к траектории и модулем реактивного ускорения. Наконец
. (2.3.12)
Таким образом, дана полная система уравнений релятивистской баллистики ракеты. В пределе малых скоростей и слабых полей они сводятся к классическим уравнениям баллистики космических ракет в ньютоновском поле.
|
|
|
|
|
|
