Погрешности звеньев и средств измерений.

Классификации погрешностей звеньев и средств измерений в целом существенно не отличаются друг от друга.

Погрешности СИ можно классифицировать по различным признакам. Сейчас наиболее употребительны следующие признаки классификации.

1. В зависимости от условий появления погрешности СИ и их отдельных измерительных звеньев делятся на 2 большие группы:

а) статические погрешности , имеющие место при статическом режиме работы, и

б) динамические погрешности , возникающие в неустановившемся режиме или имеющие место при измерении переменных во времени величин.

2. По причинам появления можно выделить следующие виды погрешностей:

а) погрешности приближения (погрешности схемы), обусловленные неполным совпадением расчетной ФП, реализуемой схемой звена, и номинальной ФП, заданной техническими условиями;

б) технологические погрешности, вызываемые технологическим разбросом размеров ВП звеньев и действием ВДФ, то есть отклонением действительной ФП от расчетной;

в) эксплуатационные погрешности, связанные с влиянием ВВ.

3. По характеру связи о входной величиной погрешности звеньев (или СИ) принято подразделять на следующие виды:

а) аддитивные погрешности , постоянные во всём диапазоне преобразования;

б) мультипликативные погрешности , линейно возрастающие или убывающие с ростом входной величины;

в) степенные составляющие , пропорциональные степеням входной величины;

г) периодические погрешности , в простейшем случае синусоидально изменяющиеся с ростом входной величины;

д) погрешность обратного хода 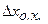, определяемая как разность значений входной величины, соответствующих одному в тому же значению выходной величины при подходе к этому значению со стороны ее больших или меньших значений;

е) нелинейные погрешности , сложным обрезом зависящие от входной величины.

В общем случае погрешность звена или СИ в целом может содержать все перечисленные выше составляющие погрешности. Тогда суммарная погрешность образуется как сумма этих составляющих (рис. 2).

4. В зависимости от размерности различают погрешности абсолютные, относительные и приведенные.

а). Абсолютная погрешность звена или СИ в целом определяется как разность между действительным значением выходной величины и его значением, определенным по номинальной ФП Эта погрешность приведена к выходу и определена в единицах выходной величины. Рассматривая эту погрешность как дифференциал от ФП

можно определить абсолютную погрешность, приведенную к входу:

где - чувствительность звена;

Рис.2 Формирование суммарной погрешности

б) Относительная погрешность определяется как отношение абсолютной погрешности к текущему значению величины:

в) Приведенная погрешность получается делением абсолютной погрешности на диапазон преобразования:

 

Относительная и приведенная погрешности часто выражаются в процентах.

5, В зависимости от характера проявления при многократных испытаниях данного звена и СИ в целом погрешности делят на систематические и случайные. Если в серии испытаний, проводимых в неизменных условиях с целью определения ФП, погрешность остается неизменной, то это означает, что она носит систематический характер. В противном случае она является случайной.

а). Систематическая составляющая проявляется одновременно со случайной составляющей. Для её выделения проводятся многократные измерения, после чего ее значение в точке х диапазона преобразования находится как

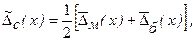
где

- среднее значение погрешности в точке х диапазона, полученное экспериментально при медленных изменениях входной величины со стороны меньших значений, и

- то же самое со стороны больших значений, (n – число измерений).

Но погрешность, систематическая для данного экземпляра измерительного звена (или СИ), становится случайной, если мы рассматриваем совокупность звеньев данного типо­размера. Тогда приходится определять статистическую оценку среднего значения систематической погрешности

 

и оценку среднего квадратического (стандартного) отклонения

Общим случаем является задание функции распределения систематической погрешности.

б) Случайная составляющая наиболее полно характеризуется законом распределения ее значений, который в общем случае изменяется с изменением входной величины. Поэтому приходится рассматривать условные законы распределения случайной составляющей погрешности. Условная функция распределения 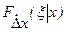выражает зависимость условной вероятности появления в эксперименте значений случайной погрешности в интервале от -∞ до текущего значения ξ от самого ξ при заданном значении x входного сигнала. (Рис. 3).

Условная плотность распределения (рис.4) является производной от условной функции распределения:

Она также изменяется при изменении величины на входе. Часто бывает достаточно охарактеризовать случайную погрешность лишь ее числовыми характеристиками. Важнейшей числовой характеристикой является дисперсия и среднее квадратическое или стандартное отклонение случайной погрешности. Его статистическая оценка вычисляется на основании экспериментальных данных как:

в) Шумы – это случайная погрешность, являющаяся случайной функцией времени и проявляющаяся в случайных блужданиях выходной величины при постоянном значении входной величины. Шумы могут генерироваться в самом звене (внутренние шумы), возникать за счет случайных флуктуаций внешних воздействий или поступать на вход звена вместе с входной величиной.

6. В зависимости от условий работы погрешность звена (и средства измерений в целом) подразделяется на основную и дополнительные.

а) Основная погрешность звена (или СИ) имеет место при нормальных условиях выполнения измерений. Нормальные условия регламентируются стандартом ГОСТ 8.050-73, входящим в систему стандартов ГСИ. Нормальные условия задаются в в форме допустимы отклонений ВВ от их номинальных значений.

Номинальные значения основных влияющих величин:

- температура окружающей среды ,

- атмосферное давление 101324,72 Па (760 мм HgS),

- относительная влажность окружающего воздуха 58 %,

- ускорение свободного падения 9,8 мс-1,

- направление линии измерения линейных размеров до 160мм у наружных поверхностей - вертикальное, в остальных случаях – горизонтальное,

- положение плоскости измерения углов – горизонтальное,

- относительная скорость движения внешней среды равна нулю,

- значение внешних сил равно нулю.

Пределы нормальной области значений ВВ устанавливаются стандартом ГОСТ 8.050-73 в зависимости от допусков не измеряемый размер и диапазона измеряемых размеров.

б) Дополнительные погрешности возникают за счет отклонения значений ВВ (или внешних возмущений) за пределы нормальной области их значений. Но при этом они должны оставаться в пределах рабочей области, устанавливаемой соответствующими стандартами. Можно говорить о частных дополнительных погрешностях, вызываемых влиянием лишь одного возмущения, или о суммарной дополнительной погрешности, обусловленной одновременным изменением всех внешних воздействий.

Наиболее подходящим для дальнейшего анализа является деление погрешностей на погрешности приближения, технологические. погрешности и эксплуатационные погрешности.

Погрешности приближения.

Общие соотношения

Погрешность приближения называется также погрешностью схемы или нелинейностью функций преобразования. Погрешность схемы возникает за счет того, что часто с целью повышения технологической точности звена используют упрощенные схемные решения, реализующие номинальную ФН лишь приближенно.

Погрешность схемы носит систематический характер, одинаковый для всех экземпляров звеньев данного типоразмера. В единицах выходной величины погрешность схемы равна разности между расчетной ФП и номинальной ФП:

Таким образом, погрешность схемы зависит от значения входной величины и от расчетных значений внутренних параметров. В качестве меры погрешности приближения используются следующие показатели:

I). Наибольшее отклонение в диапазоне преобразования расчетной функции преобразования от номинальной ФП

Расчетные значения внутренних параметров находятся при этом путем минимизации наибольшего отклонения. Такой способ приближения называется равномерным приближением.

2) Среднее квадратическое отклонение расчетной функции преобразования от номинальной ФП:

 

где p(x) - плотность распределения измеряемой величины. Если она заранее неизвестна, то в большинстве случаев для приборов с малым диапазоном измерений её можно считать равномерной в диапазоне измерения

и тогда

Расчетные значения внутренних параметров находятся путем минимизации средней квадратической погрешности или дисперсии .

Такой способ приближения называется приближением в среднем квадратическом.

Рассмотрим теперь математический аппарат, применяемый при этих способах приближения.

Равномерное приближение

Отличается использованием аппарата полиномов Чебышева, наименее отклоняющихся от нуля в диапазоне [-1; +1] среди всех других полиномов той же степени. Соберем в таблицу несколько первых полиномов Чебышева степени n=1, 2, …., 5, нормированные таким образом, чтобы коэффициенты при старшей степени переменной равнялись единице.

 

n	Полином Чебышева	Наибольшее отклонение	Точки наибольших отклонений	Корни полинома
		0,5000	0; ±1	±0,7071
		0,2500	±0,5; ±I	0; ±0,866
		0,1250	0; ±0,7071; ±1	±0,3827; ±0,9239
		0,0625	±0,309; ±0б809; ±1	0; ±0,5878; ±0.9511

 

Графически эти полиномы представлены на рис. 5.

 

Возможны две методики приближения.

I) Функцию преобразования можно разложить в степенной ряд Тейлора в середине диапазона преобразования :

где

Делаем замену переменных:

Поскольку изменяется в пределах от до , то переменная будет теперь изменяться в диапазоне [-1; +1]. В результате получаем:

Погрешность приближения при линейной номинальной функции преобразования

составляет

Таким образом, мы представили погрешность приближения в форме полинома от переменной в диапазоне ее изменения от –1 до +1. Всегда, уже по внешнему виду функция преобразования, можно судить о том, какой степенью этого полинома можно ограничиться. Во всяком случае, при предварительном анализе можно ограничиться степенью и затем уточнить решение.

Ограничиваясь третьим членом разложения, приведем выражение для к форме, сопоставимой с полиномами Чебышева. Для этого вынесем коэффициент за скобки:

Для того, чтобы стоящей в квадратных скобках полином был действительно полиномом Чебышева, необходимо выполнение следующих условий:

 

Исходя из этих условий, можно теперь выбирать расчетные значения ВП, входящих в выражение для ФП. Наибольшее значение погрешности схемы получается при этом равным:

Пример. Синусный механизм обладает расчетной функцией преобразования

 

которая раскладывается в степенной ряд относительно точки следующим образом:

поскольку

Пусть функция преобразования должна иметь вид:

а диапазон преобразования

Первое и третье условия выполняются автоматически. Второе условие приводит к выражению

Полученное решение и является искомым значением расчетного параметра, то есть плеча синусного рычага. Это решение получено из условия равномерного приближения ФП синусного механизма к линейной ФП (в диапазоне ±0,5 мм).

Наибольшее значение погрешности приближения составляет:

или в единицах входной величины

2) Вторая методика приближения не требует предварительного разложения функция преобразования в степенной ряд и основывается на использовании корней полинома Чебышева.

Если решен вопрос о выборе степени аппроксимирующего полинома Чебышева, то погрешность схемы должна обратиться в нуль в точках диапазона, соответствующих корням полинома Чебышева. Поэтому расчетные значения внутренних параметров можно найти из соотношений:

при всех ( - корни полинома).

Пример:

Для синусного механизма

Поэтому параметр можно найти из условия равенства значений расчетной и номинальной функций преобразования при =±0,866:

Поэтому

Погрешность приближение составляет при этом:

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: