 |
Функция полезности. Переход от кардинализма к ординализму
|
|
|
|
Количественная (кардиналисткая) функция полезности – это функция полезности, возникающая в том случае, когда мы не только можем определить расстановку и последовательность классов безразличия, но и указываем, как мы оцениваем разность в уровнях благосостояния, соответствующих каждому из таких классов безразличия. При этом можно будет сравнивать не только сами значения функции полезности, но и их изменения. Фактически это означает, что данный потребитель в данной ситуации оказывается в состоянии определить не только свои предпочтения как таковые, но и их интенсивность, поскольку он определяет разницу или равенство в степени удовлетворенности различных наборов. При этом сами количественные оценки таких разностей в уровнях благосостояния не имеют абсолютного значения. Эта функция, несмотря на ее ограниченность (только линейными функциями) дает нам взамен возможность оценивать количественные различия между разными уровнями благосостояния данного потребителя в данной ситуации с точностью до линейного преобразования.
Однако практика показала и большой недостаток кардиналистскогоподхода к измерению полезности. В частности, практика выяснила тот факт, что полезность нельзя измерить количественно. Этот вывод сделал итальянский экономист Вильфредо Парето (1848 – 1923). То есть, вывод Парето, практически означал отказ от концепции предельной полезности в ее первоначальном виде. Одновременно это подвигло многих экономистов поиску новых способов объяснения потребительского поведения на основе более реалистических допущений, сближающих теоретическое объяснение с практикой.
Суть этих допущений состояла в следующем. Как известно из повседневной практики, многие товары взаимосвязаны друг с другом в процессе потребления: некоторые товары могут потребляться только совместно (они называются «комлементарными»), другие, наоборот, служат удовлетворению одной и той же потребности и являются в той или иной степени взаимозаменяемыми (товары – «субституты). Следовательно, правильнее рассматривать полезность не от потребления отдельно взятого товара, а от всего набора потребляемых товаров. Это открывает возможность оценивать полезность не с количественной точки зрения, а с точки зрения порядка предпочтений наборов товаров. Так совершился переход «кадиналистского» (т.е. количественного) подхода к полезности – к «ординалистскому» (т.е. порядковому).
|
|
|
Первые шаги в этом направлении были сделаны российским экономистом Е. Е. Слуцким (1880 – 1948) в статье «К теории сбалансированного бюджета потребителя». Окончательное оформление ординалистский подход получил в работе Роя Аллана (1906 – 1983) и Джона Р. Хикса (1904 – 1989) «Пересмотр теории ценности» (1934).
Центральная идея ординалистского подхода может быть объяснена следующим образом. Теория отказывается от представления о том, что потребитель способен количественно измерить полезность, извлекаемую из некоторого набора товаров, а предполагает, что он может просто сравнить различные наборы товаров с точки зрения их предпочтительности. При этом более предпочтительны наборы товаров, имеющие более высокий уровень полезности, и равноценные наборы, имеющие одинаковый уровень полезности. Другими словами, наш потребитель не мучается вопросом количественной оценки полезности товара. Не требуется от него при выборе набора товаров и ответ на вопрос, во сколько данный набор полезнее всякого другого. Потребитель на основе своей субъективной оценки выносит решение, что данный набор товаров для него предпочтительнее всех прочих.
|
|
|
Порядковая (ординалистская) функция полезности выражает только определенную последовательность, порядок, в котором располагаются классы безразличия или группы равноценных для потребителя наборов благ (благ, обладающих одинаковой полезностью), например, от менее предпочтительных к более предпочтительным. Ее можно образовать с помощью любого последовательного множества чисел, соответствующих данным классам безразличия таким образом, что число, поставленное в соответствии более предпочтительному классу безразличия, будет больше числа, поставленного в соответствие менее предпочтительному классу безразличия. Тогда значения такой порядковой функции и будут выражать только расстановку (ранжирование последовательность, порядок) определенных групп равновесных наборов благ.
U (A) > U(Б); U(A) < U(Б) либо U(A) = U (Б).
Чаще всего для установления значений ординалистской функции полезности используют последовательность натуральных чисел, начиная с единицы, например:
U(A) =1; U(Б) = 2; U(В) = 3 и т.д.
При этом сами значения порядковой функции полезности выстраиваются в аналогичную последовательность:
U1, U2, U3 … Un.
Таким образом, с практической точки зрения потребитель с порядковой функцией всегда может сказать, что чему он предпочитает, но не может определить, насколько один набор лучше другого.
Таким образом, преобразовав субъективную теорию полезности в общую логику выбора, Р. Аллан и Д. Хикс значительно сблизили теоретическую базу с практическим поведением потребителя. Закономерности этого поведения уже не связаны с измерением полезности. Их исследование базируется на наблюдаемых эффектах «замещения» и эффекта «дохода».
Тем не менее, экономисты эффективно используют обе функции полезности. Даже кардиналистскую (количественную).
В частности, используя количественную (кардиналистскую) функцию полезности, можно охарактеризовать не только общую полезность, но и предельную полезность – т.е. дополнительное увеличение данного уровня благосостояния, получаемое при потреблении дополнительного количества блага данного вида и неизменных количествах потребляемых благ всех остальных видов. Экономисты обозначают ее как MU – marginal utilitу.
|
|
|
∆U
MU = ──, где
∆X
MU – предельная (приростная, дополнительная) полезность;
∆U – изменения полезности (прирост или уменьшение);
∆Х – изменения количества потребляемого блага (прирост или уменьшение).
Теория предельной полезности строится на предположениях:
1) предельная полезность – это не наибольшая и не средняя полезность, а именно наименьшая полезность, ради получения которой эта вещь может использоваться.
2) потребитель стремится получить максимальное удовлетворение (полезность), используя свой ограниченный доход;
3) за относительно короткий период времени, в течение которого вкусы потребителей не изменятся, предельная полезность каждой последующей единицы продукции падает, так как потребность в этом конкретном продукте постепенно удовлетворяется, или «насыщается». Так, экономисты открыли и сформулировали закон убывающей предельной полезности.
Закон убывающей предельной полезности гласит, что мере того, как вы потребляете все новые единицы одного и того же товара, растет общаяполезность (TU), получаемая вами, но при этом она возрастает все более медленными темпами вследствие того, что предельная полезность (MU) данного товара имеет тенденцию к сокращению.
Так, если потребление первого бутерброда принесет человеку полезность, равную, положим, 5 ютилям, второго – 4, третьего – 2, а четвертого – 1 ютилю, то общая полезность этого ряда составит 12 ютилей (а предельная полезность будет равна 1) Отказ от каждого последующего бутерброда будет означать уменьшение общей (суммарной) полезности и одновременное увеличение предельной полезности последнего бутерброда. Например, если отказаться от четвертого бутерброда, то общая полезность (TU) составит 11 единиц, а предельная полезность (MU), при отказе от третьего бутерброда TU составит 9 единиц, а MU возрастет до 4, и т.д.
То есть, если общая полезность (TU) растет до известного предела, то предельная полезность сразу начинает падать. Эта динамика изображена на рисунке 5.
|
|
|
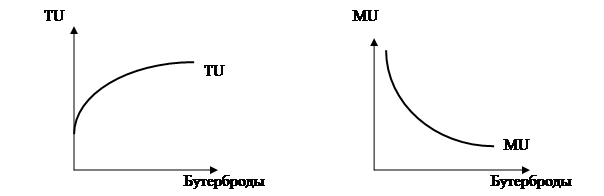
Рис.5. График общей (TU) и предельной полезности (MU)
Этот закон может быть представлен с помощью таблицы.
Таблица 2
| Количество потребленного товара | Общая полезность | Предельная полезность |
| (4 – 0 = 0) | ||
| (7 – 4 =3) | ||
| (9 – 7 = 2) | ||
| (10 – 9 = 1) | ||
| (10 – 10 = 0) |
Из таблицы видно, что хотя общая полезность увеличивается до 10, темпы этого увеличения все время снижаются. Это означает, что предельная полезность будет сокращаться. Снижение предельной полезности связано с уменьшением субъективной оценки потребителем единицы товара, когда возрастает количество приобретенных единиц этого блага. Или, еще проще: полезность обратно пропорциональна количествупотребляемого блага.
Каждая последующая партия блага удовлетворяет все менее насущную потребность людей, поэтому ее оценки все меньше. Если блага не хватает на менее насущные потребности, а хватает только на более насущные потребности, то оценка этого блага выше и определяется оценкой последней его партии.
Таким образом, человек дает ту или иную оценку вещи в зависимости от того, какую пользу она ему приносит. Если, например, человеку для удовлетворения его производственных и личных потребностей необходимо иметь 10 ведер воды, а в его распоряжении имеется 50, то излишек воды в 40 ведер не будет обладать никакой ценностью. Если же у него останется только 10 ведер воды, то каждое из них приобретет ценность, ибо лишение хотя бы одного из них не позволит человеку удовлетворить ту или иную потребность. Именно поэтому предельная полезность – это не наибольшая и не средняя полезность, а именно наименьшая польза, ради получения которой эта вещь еще может рациональным образом употребляться.
Математически, общая полезность равна сумме предельных полезностей:
TU = ∑ MU
Например, TU5 = MU1-5 = 4 + 3 + 2 + 1 = 10
В свою очередь: MU = TUn +1 – TUn.
В таблице для этого необходимо – от значения нижней строчки (колонки 2) отнять значения верхней строчки той же колонки.
Например, MU4 = 10 – 9 = 1.
По данной таблице и строятся кривые TU и MU.
Убывающая предельная полезность помогает также объяснить закон убывающего спроса. Дело в том, что линия спроса совпадает с кривой предельной полезности. С увеличением количества предлагаемого товара цены на каждую единицу падают. Это объясняется тем же – каждая добавляемая порция товара удовлетворяют все менее настоятельную потребность, и ценится меньше, чем предыдущие. Именно этим объясняется необходимость понижения цены, чтобы побудить потребителя к увеличению покупок такого товара.
|
|
|
Как может быть использован закон убывающей предельной полезности при объяснении потребительского выбора? Предположим, что мы пришли в магазин за покупками, имея 350 рублей. Предположим также, что имеется всего два товара: А и Б, цены которых соответственно 50 и 100 руб. Сколько единиц товара А и Б мы купим? Иными словами исходя из их полезности?
Оценим предельную полезность товаров А и Б в баллах исходя из наших субъективных представлений и поместим в соответствующие графы таблицы 3. Согласно нашей оценке, наибольшее удовлетворение нам принесет покупка товара Б. Однако мы учитываем не только предельную полезность, но и цену товара А. Мы принимаем решение о покупке, исходя из полезности на единицу затраченных средств, т.е. на 1руб.
Таблица 3
| Количество, шт. | Товар А (цена 50 руб.) | Товар Б (цена 100 руб.) | ||
| Предельная полезность MU | Предельная полезность на 1 руб. MU/P | Предельная полезность | Предельная полезность на 1 руб. MU/P | |
| 0,1 | 0,09 | |||
| 0,08 | 0,06 | |||
| 0,06 | 0,05 | |||
| 0,04 | 0,03 | |||
| 0,02 | 0,01 |
Данные предельной полезности на 1 руб. будут иными, поэтому максимально удовлетворит наши потребности покупка трех единиц товара А и двух единиц товара Б. Или: TU = 12 (5 + 4 + 3) + 15(9 + 6) = 27 ютилей.
Любая другая комбинация количеств товаров А и Б при существующих ценах и определенном размере имеющихся в наличии средств (350 руб.) даст меньшую суммарную полезность для покупателя.
Потребительское равновесие достигается, когда отношения предельных полезностей отдельных товаров к их ценам равны. Или математически это можно выразить формулой:
MUA / MUБ = PA / PБ.
После преобразования, используя свойства пропорций, мы получим формулу максимизации полезности.
MUA MUБ MUN
──── = ──── = … = ────
PA PБ PN
В нашем примере 3: 50 = 6: 100 = 0,06. Эта формула используется, таким образом, для определения условий (цены и объема покупок) равновесия покупателя, то есть условий, при которых он получает максимальную полезность в рамках своего бюджета. Математически – это значит, найти такие пары значений в таблице, у которых результат дроби одинаковый. У нас это 0,06.
Что произойдет, если цена товара Б снизится вдвое? Тогда на те же 350 рублей мы купим три единицы товара А и четыре единицы товара Б.
Эту же формулу можно вывести из графика кривых безразличия (изоквант) и изокост. Она, в частности, является выражением условий, при которых изокоста является касательной линией к изокосте (через тангенс равного угла наклона изокванты и изокосты).
Правило максимизации полезности гласит: потребитель может максимизировать полезность таким образом, чтобы последний рубль, израсходованный на продукт А, а также последний рубль, израсходованный на продукт Б и т.д., принесут ему одинаковое количество добавочной или предельной полезности.
Уравнение утверждает, что потребитель, максимизирующий полезность, покупает два товара таким образом, что их предельные полезности в расчете на 1 рубль равны.
Общее условие равновесия потребителя (эквимаржинальный принцип или принцип равной полезности) указывает, что потребитель в равновесии распределяет расходы на все товары таким образом, чтобы уравнять предельную полезность, приходящуюся на 1 рубль, затрачиваемый на каждый из товаров.
Теперь воспользуемся ординалистским подходом для определения условий равновесия потребителя. Инструментом такого анализа являются кривая безразличия (изокванта) и кривая равной стоимости (изокоста или бюджетная линия).
|
|
|


