Характеристики режима резания и сечения срезаемого слоя

К числу основных характеристик режима резания относятся глубина резания t и глубина врезания е, подачи на оборот S₀, на зуб S_Z, минутная подача S_м, скорость резания v.

Глубина резания t характеризует величину врезания режущей кромки, измеренную перпендикулярно рабочей плоскости. При прямых срезах, т. е. при , глубина резания вместе с углом в плане определяет ширину срезаемой стружки (см. рис. 13.2, а).

При обратных срезах, т. е. при , глубина резания более тесно связана с толщиной срезаемого слоя.

При торцовом фрезеровании на вертикально-фрезерном станке (см. рис. 13.6) рабочая плоскость расположена горизонтально и глубина резания измеряется перпендикулярно этой плоскости, т. е. вдоль оси вращения фрезы. При цилиндрическом фрезеровании (см. рис. 13.6, рис. 13.20) рабочая плоскость расположена вертикально. Глубина резания и в этом случае измеряется вдоль оси вращения фрезы, но в горизонтальной плоскости.

Глубина врезания е измеряется в рабочей плоскости в направлении, перпендикулярном подаче. Этот параметр рассматривают только для таких способов обработки, в которых угол между векторами скорости резания и подачи изменяется, например для торцового и цилиндрического фрезерования. Глубина врезания инструмента е вместе с его диаметром D характеризует путь режущего лезвия за один оборот, часть траектории, при прохождении которой зуб находится в контакте с деталью.

Подача характеризуется несколькими различными параметрами. Скорость подачи, как правило, измеряют в миллиметрах в минуту (мм/мин) и называют минутной подачей S_м. Кроме минутной подачи S_м используют подачу S₀ на один оборот инструмента (или детали) (мм/об) или подачу на один двойной ход (мм/дв. ход), а также подачу на одно режущее лезвие или зуб (мм/зуб) – подачу на зуб S_Z.

Все три перечисленные характеристики измеряют в направлении движения подачи S_м, а следовательно, в рабочей плоскости. Они связаны между собой следующими соотношениями:

, (13.1)

, (13.2)

где n – частота вращения; Z – число зубьев (режущих лезвий) инструмента.

Поскольку в общем случае подача не перпендикулярна скорости резания v и, следовательно, не обязательно находится в основной плоскости, целесообразно рассматривать также нормальную к скорости резания составляющую подачи S_Z– подачу S_q.

. (13.3)

Для точения, например,

(13.4)

а минутная подача

. (13.5)

Скорость резания v при вращательном движении инструмента или детали рассчитывается по формуле

(13.6)

где D и n – диаметр и частота вращения инструмента или детали.

При прямолинейном движении, например при строгании с длиной хода ползуна L и частотой n, скорость резания v определяется следующим образом:

. (13.7)

При значительном превышении длины главной режущей кромки в сравнении с длиной зачищающей (вспомогательной) кромки, т. е. при

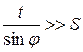, (13.8)

 

отклонением скорости v₁ от нормали можно пренебречь (n = 0),а угол y

 

между диагональю АС и подачей считать равным углу в плане j. При этом приближенное (статическое) значение ширины срезаемого слоя b_c вычисляется по простой формуле

. (13.9)

При косоугольном резании (т. е. когда угол l не равен нулю) ширина срезаемого слоя будет несколько больше:

. (13.10)

Толщина срезаемого слоя a может быть охарактеризована: действительной толщиной a_д, действительной максимальной толщиной а_м, действительной средней толщиной а_ср, статической толщиной срезаемого слоя а_с.

Действительная толщина срезаемого слоя a_д измеряется в основной плоскости в направлении скорости стружки v₁, т. е. перпендикулярно диагонали сечения срезаемого слоя. Поскольку в направлении скорости v₁ расстояние между ломаными линиями АВС и ADC переменно, то и действительная толщина срезаемого слоя может быть переменной по ее ширине.

При прямоугольном резании (l = 0)и выполнении условия (13.10) толщина срезаемого слоя приближенно оценивается статической толщиной срезаемого слоя а_с = BF, измеренной в направлении нормали к проекции главной режущей кромки:

. (13.11)

 

При свободном резании (одной прямолинейной режущей кромкой), а также при несвободном резании, не вызывающем отклонения вектора стружки v₁ от нормали к проекции главной режущей кромки на основную плоскость (например, при отрезке, сверлении и др.), используют статические значения толщины и ширины срезаемого слоя (y = j, n = 0).

 

 

14. ДЕФОРМАЦИИ, СИЛЫ И ТЕМПЕРАТУРЫ ПРИ РЕЗАНИИ

14.1. Схематизация стружкообразования и характеристики
деформаций при резании

Упрощенная схема зоны деформации с единственной плоскостью сдвига для образования сливной (сплошной, непрерывной) стружки предложена русским ученым – профессором И. А. Тиме (рис. 14.1).

 

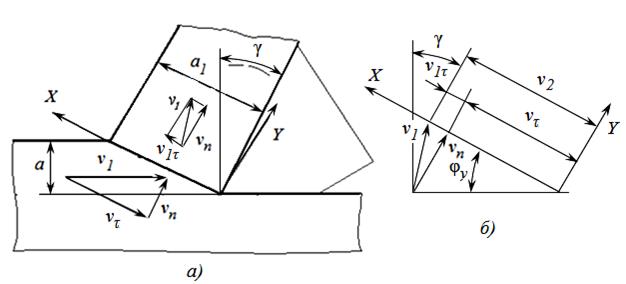
Рис. 14.1. Соотношения между скоростями стружки и детали при деформации
по схеме И. А. Тиме (с единственной плоскостью сдвига):
а – схема зоны стружкообразования; б – план скоростей

 

В силу условия непрерывности (сплошности) несжимаемой деформируемой среды при образовании сливной стружки при плоской деформации проекции скорости резания и скорости стружки на нормаль к условной плоскости сдвига должны быть равны друг другу (рис. 14.1, б):

, или . (14.1)

Из формулы (14.1) следует

. (14.2)

Отношение скорости резания v к скорости стружки v₁ называют усадкой стружки z.

Вследствие постоянства объема 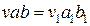и равенства ширины стружки ширине срезаемого слоя усадка стружки может быть определена и как отношение толщины стружки а₁ к максимальной толщине срезаемого слоя а_м:

_. (14.3)

Условие контакта стружки с инструментом требует, чтобы проекции скоростей стружки и резца (или детали) на нормаль к передней поверхности режущего лезвия были равны друг другу (рис. 14.2):

, откуда . (14.4)

 

Рис. 14.2. Схема скоростей резца и стружки при строгании:
1 – инструмент; 2 – стружка; 3 – обрабатываемый металл

 

Отношение скорости v₂, полученной из условия контакта стружки с резцом, к нормальной относительно условной плоскости сдвига составляющей скорости резания v_n = v·sinj_y называют относительным сдвигом e:

(14.5)

Используются и другие выражения для относительного сдвига e, тождественные (14.5):

γ

(14.6)

При прохождении материала через зону стружкообразования (плоскость сдвига) квадрат, сориентированный согласно рисунку 14.3, преобразуется в параллелограмм, а вписанная в него окружность – в эллипс.

 

 

Рис. 14.3. Схема образования текстуры стружки

 

Угол y между большой осью эллипса и направлением сдвига называют углом текстуры:

. (14.7)

Фактически при образовании непрерывной и сплошной (сливной) стружки зона деформации не является плоскостью, а имеет более сложную форму и условно может быть разбита на несколько зон (рис. 14.4).

Рис. 14.4. Схема зоны деформации (а): A – зона стружкообразования с параллельными
границами; Б – застойная зона адиабатических деформаций, поперечное сечение «уса»; В и Г – зоны контактных деформаций на передней и задней поверхностях;
распределение скоростей в зоне А (б)

Непрерывное изменение скоростей при переходе деформируемой частицы через зону стружкообразования с параллельными границами может быть достаточно хорошо аппроксимировано функциями вида:

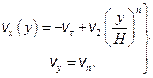(14.8)

Здесь n – показатель степени, характеризующий неоднородность распределения касательной скорости v_x(y) в зоне стружкообразования и, следовательно, неоднородность сдвига.

Скорость деформации сдвига

. (14.9)

В частности, у конечной границы зоны деформации при приближении к ней со стороны зоны стружкообразования, т. е. при y, стремящемся к (H→0), скорость деформации максимальна:

(14.10)

Для средних условий резания: e = 2,5, v = 1 м/с, j_у = 30°, n = 5,
H = (0,2–0,5) a при a = 0,2 мм

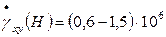, c^–1. (14.11)

В сравнении со стандартными механическими испытаниями на растяжение, сжатие, при которых скорость деформации приблизительно равна 10^–4–10^–3 с^–1, и даже в сравнении со скоростями деформаций при различных методах обработки металлов давлением, достигающими 10²–10^–2 с^–1, скорости деформации при резании очень велики.

Закон изменения истинных деформаций в зоне стружкообразования может быть получен интегрированием скоростей деформации:

(14.12)

Согласно (11.13) деформация в зоне стружкообразования может рассматриваться как неоднородный сдвиг.

Наибольшего значения истинный сдвиг достигает при y = H, т. е. у конечной границы зоны стружкообразования: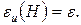

Силы при точении

К технологическим силовым характеристикам точения относят: составляющую силы резания P_Z, направленную по скорости резания v, проекцию P_X силы резания на направление подачи S, перпендикулярную названным направлениям, силу P_Y, а также крутящий момент M _кр и мощность резания N_e.

Сила P_X (рис. 14.5)нагружает механизм подачи станка и ограничивается прочностью наиболее слабых звеньев этого механизма. Сила P_Y отжимает резец в направлении, перпендикулярном обработанной поверхности. Величина этой силы ограничивается требованиями к точности обработки, а также виброустойчивостью процесса резания.

Рис. 14.5. Схема технологических осей x, y, z
и технологических составляющих P_X, P_Y, P_Z силы резания
при продольном точении

 

Силу P_Z, перпендикулярную основной плоскости, часто называют главной составляющей силы резания. Это связано с тем, что она, как правило, превышает по величине силы P_X и P_Y и, кроме того, совпадая по направлению со скоростью резания, определяет мощность резания N_e (кВт):

(14.13)

Вместе с диаметром D обработки сила P_Z определяет также крутящий момент (Н·м):

(14.14)

Силы P_X, P_Y, P_Z, крутящий момент M _кр, мощность резания N_e необходимо знать при определении допускаемых режимов резания, а также при проектировании станков, приспособлений и металлорежущих инструментов.

При сверлении, зенкеровании, развертывании в качестве технологических составляющих используются осевая сила и крутящий момент. При торцовом фрезеровании с вертикальной осью вращения фрезы используют крутящий момент, осевую силу P_W (вертикальную) и две силы в горизонтальной плоскости – силу подачи P_H и перпендикулярную ей силу P_V.

Физические составляющие силы резания относят к тем площадкам (или зонам), где они в действительности возникают, т. е. к условной плоскости сдвига, к передней и задней поверхностям режущего инструмента и застойной зоны. Таким образом, при этом раздельно учитываются силы на передней и задней поверхностях инструмента (рис. 14.6).

 

 

Рис. 14.6. Физические составляющие силы резания в основной (а) плоскости,
плоскостях резания (б) и стружкообразования (в)

 

Раздельно рассматриваются также силы на главной и вспомогательной задних поверхностях. Для повышения точности расчета сил целесообразно раздельно учитывать силы на задних поверхностях застойной зоны и фаски износа.

Методика расчета сил резания в каждом конкретном случае должна учитывать закономерности и специфику рассматриваемого способа обработки. По числу, форме и расположению режущих кромок точение может представлять собой одну из четырех разновидностей лезвийной обработки: свободное прямоугольное, несвободное прямоугольное, свободное косоугольное и несвободное косоугольное резание. Каждая из названных схем имеет свои особенности, которые проявляются главным образом в положении плоскости стружкообразования относительно системы технологических координат x, y, z.

Наиболее простым является случай свободного прямоугольного резания, когда резание осуществляется одной прямолинейной кромкой, перпендикулярной к скорости резания v (рис. 14.7).

 

Рис. 14.7. Положение плоскости стружкообразования и схема сил
при свободном прямоугольном точении

 

При свободном прямоугольном точении плоскость стружкообразования перпендикулярна режущей кромке, т. е. совпадает с главной секущей плоскостью, и содержит векторы скоростей схода стружки v ₁и резания v.

Введем систему координат n, m, x,связанную с плоскостью стружкообразования. Ось n совпадает с проекцией вектора скорости схода стружки на основную плоскость, а ось x – с вектором скорости резания. При этом третья ось координат m направлена вдоль режущей кромки резца. Силы на задней поверхности (F ₁ и N ₁), определяющиеся в главной секущей плоскости (рис. 14.7), и проекции силы стружкообразования (R _n и R _x), определяющиеся в плоскости стружкообразования, в данном случае находятся в одной плоскости. Проекция силы резания на ось m равна нулю.

 

Рис. 14.8. Схема сил в условной плоскости сдвига и на укороченной
передней поверхности резца со стабилизирующей фаской

 

Расчет технологических составляющих силы стружкообразования для условий пластического контакта стружки с инструментом целесообразно основывать на том, что в первую очередь определяются две касательные силы (рис. 14.8):

, (14.15)

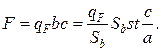(14.16)

Относительная длина контакта с/а для схем резания инструментами со стабилизирующей фаской определяется по ширине фаски и действительному углу схода стружки:

(14.17)

При резании инструментом с полной передней поверхностью может быть использована формула

(14.18)

Нормальную к передней поверхности составляющую силы стружкообразования найдем, проектируя на условную плоскость сдвига силы , действующие на стружку со стороны условной плоскости сдвига, силы F и N, действующие на стружку со стороны передней поверхности:

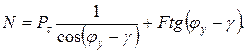(14.19)

Силы 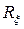и найдутся как проекции сил F и N на оси x и n:

(14.20)

где 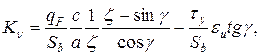(14.21)

(14.22)

Выразим силы N ₁ и F ₁ через нормальные напряжения q_{N 1} и коэффициент трения m₁ на задней поверхности инструмента:

(14.23)

Согласно экспериментальным данным, для резания сталей на ферритной основе твердостью HB < 3000 МПа без применения смазочно-охлаждающих жидкостей можно принять

.

 

С учетом вышеизложенного формулы для определения сил P_X, P_Y, P_Z при свободном прямоугольном точении имеют вид:

(14.24)

⇐ Предыдущая29303132333435363738Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: