 |
Задание С-3. Определение центра тяжести фигуры
|
|
|
|
Задание С-1. Определение реакций опор балки
Конструкция, состоящая из двух прямолинейных стержней, жестко скрепленных между собой в точке С, расположена в вертикальной плоскости. На конструкцию действует пара сил с моментом М, распределенная нагрузка интенсивностью q и одна сила, указанная в таблице. Определить реакции связей конструкции, вызванные заданными нагрузками.
Исходные данные: F 3 = 30 кН (в т. Е), a 3 = 60 °, М = 100 кН×м, q = 20 кН/м, а = 0,2 м.
Определить: 
| В |
| q |
| А |
| М |
| С |
| 5 а |
| K |
|
| a 3 |
| 60° |
| 3 а |
| 3 а |
| 4 а |
| Е |
Решение.
Рассмотрим равновесие балки АСB, состоящая из двух прямолинейных стержней, жестко скрепленных между собой в точке С.
Балка нагружена парой сил с моментом М, сосредоточенной силой 
, равномерно распределенной нагрузкой с интенсивностью 
,которую заменим ее равнодействующей 
, приложенной в середине нагружаемого участка АК и равной по величине:
В точке В балка закреплена неподвижным цилиндрическим шарниром. Реакцию шарнира А ‒ 
представим ее проекциями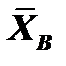 
, 
, направленными параллельно выбранным координатным осям. В точке А балка опирается на шарнирно подвижную опору. Реакция 
направлена перпендикулярно опорной поверхности.
Балка находится в равновесии под действием плоской произвольной системы сил, для которой справедливы три условия равновесия. Запишем условия равновесия плоской произвольной системы сил и составим уравнения равновесия:
(1)
(2)
(3)
Из (3) уравнения:
Из (1) уравнения:
Из (2) уравнения:
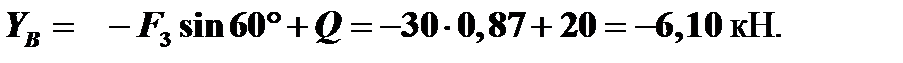
| x |
|
|
|
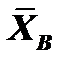
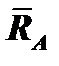
| y |
|
| 60° |
| F 3·cos60° |
| В |
| А |
| М |
| С |
| 2,5 а |
| K |
|
|
| 60° |
| 3 а |
| 3 а |
| 4 а |
| Е |
| 2,5 а |
 |
|
|
|
Для проверки правильности решения составим уравнение моментов относительно точки Е:
Следовательно, задача решена верно.
Ответ. 
Знак «минус» указывает на то, что истинное направление реакции противоположно показанному на расчетной схеме.
Задание С-2. Определение реакций опор твердого тела
Две однородные прямоугольные пластины, приваренные под прямым углом друг к другу, образуют угольник, который закреплен с помощью различного типа связей. Размеры пластин в направлениях параллельных координатным осям x, y, z, равны соответственно 2 l, 3 l и l. Вес большей из пластин равен ‒ G 1, вес меньшей ‒ G 2. Каждая из пластин расположена параллельно одной из координатных плоскостей.
Определить реакции связей.
Исходные данные: F 1 = 10 кН (в т. D), a 1 = 60 °, F 4 = 40 кН (в т. E), a 4 = 30 °, G 1 = 5 кН, G 2 = 2 кН, М = 10 кН×м, l = 0,5 м.
Определить: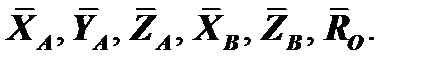 
Решение.
Рассмотрим равновесие изогнутой плиты,находящейся под действием пространственной произвольной системы сил.
На плиту действуют заданные силы: 
, 
, 
, 
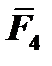,пара сил с моментом М.
Плита закреплена связями:
‒ в точке А – сферический шарнир, реакцию которого представляем тремя составляющими 
направленными по заданным координатным осям;
‒ в точке В ‒ подшипник, реакция которого лежит в плоскости перпендикулярной оси вращения шарнира и представляется двумя составляющими 
;
‒ в точке О ‒ стержень, реакцию 
которого направляем вдоль стержня к плите, предполагая, что стержень сжат.
| y |
| z |
| x |
| 3 l |
| B |
| 2 l |
|
|
| О |
| A |
|
|
|
|
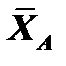
| E |
| D |
|
|
|
|
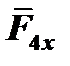
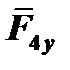
| a 4 |
|
|
| M |
| a 1 |
|
|
|
 |
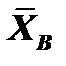
2. Составляем шесть уравнений равновесия действующей на плиту пространственной произвольной системы сил:
(1)
(2)
(3)
(4)
(5)
(6)
Из уравнения (6) определяем XB:
Из уравнения (1) определяем XA:
Из уравнения (2) определяем YA:
|
|
|
Из уравнения (5) определяем RO:
Из уравнения (4) определяем ZB:
Из уравнения (3) определяем ZA:
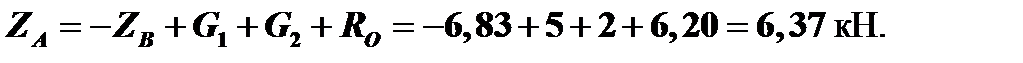
Ответ: 
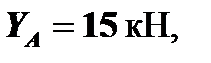
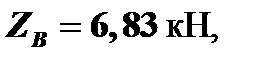
Знак «минус» указывает, на то, что истинное направление составляющей реакции 
противоположно показанному на рисунке.
Задание С-3. Определение центра тяжести фигуры
Две однородные прямоугольные пластины, приваренные под прямым углом друг к другу, образуют угольник. Размеры пластин в направлениях параллельных координатным осям x, y, z, равны соответственно 2 l, 3 l и l. Каждая из пластин расположена параллельно одной из координатных плоскостей.
Из угольника вырезана фигура в виде прямоугольного треугольника. Вычислить координаты центра тяжести пространственной фигуры в виде угольника с вырезом для обозначенной на рисунке системы координат. Толщиной пластин пренебречь.
Исходные данные: DN = 4 l, AB = 2 l, AE = 3 l, l = 0,5 м.
Определить: 
Решение.
1. Для решения задачи применяем метод разбиения тела на части, центры тяжестей которых легко определяются, с использованием способа отрицательных площадей. Вырезанный треугольник будем считать телом с отрицательной площадью:
1 – прямоугольник ABDE (центр тяжести С 1),
2 – прямоугольник DEON (центр тяжести С 2),
3 – треугольник EON (центр тяжести С 3).
| D |
| y 1= y 2 |
| y 3 |
| x 1 |
| y |
| z |
| x |
| 3 l |
| B |
| 2 l |
| О |
| A |
| E |
| N |
| C 1 |
| C 2 |
| C 3 |
    |
2. Вычислим площади составных частей и определим координаты их центров тяжести.
1) Прямоугольник ABDE:
S 1 = 2 l · 3 l = 6 l 2 = 6 · 0,52 = 1,5 м2, х 1 = l = 0,5 м, у 1 = 1,5 l = 1,5·0,5 = 0,75 м, z 1 = - l = - 0,5 м.
2) Прямоугольник DEON:
S 2 = l · 3 l = 3 l 2 = 3 · 0,52 = 0,75 м2, х 2 = 0, у 2 = 1,5 l = 1,5·0,5 = 0,75 м, z 2 = - 0,5 l = - 0,25 м.
3) Треугольник EON:
3. Вычисляем координаты центра тяжести фигуры по формулам:
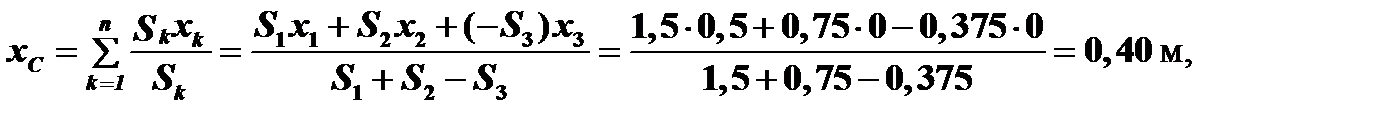
Ответ: xС = 0,40 м, yС = 0,80 см, zC = - 0,47 м.
|
|
|
