 |
Задание K-1. Определение кинематических характеристик движения
|
|
|
|
Материальной точки
По заданным уравнениям движения точки x = f 1(t), y = f 2(t) найти уравнение траектории точки, для момента времени t 1 = 1 c вычислить ее скорость. Нормальное, касательное и полное ускорения, а также радиус кривизны траектории. На рисунке в масштабе построить траекторию движения точки и для заданного момента времени построить вектора скорости и ускорения.
Дано: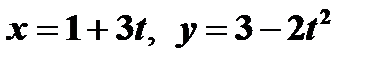 
(x,y ‒ см, t ‒ с), t 1 = 1 c.
Определить: y = f (x), 
r 1.
Решение.
1. Определяем траекторию движения точки и ее положение в заданный момент времени. Для этого из уравнений движения точки исключаем параметр t:
При t 0 = 0 имеем:
При t 1 = 1c имеем:
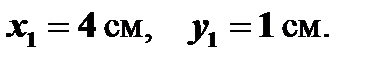
То есть траектория движения точки ‒ часть параболы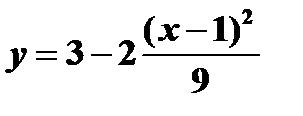 
. На рисунке в масштабе строим траекторию движения.
2. Определяем скорость точки.
При координатном способе задания движения вектор скорости точки определяется:
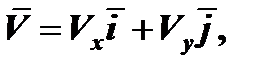
где Vx – проекции вектора скорости на ось x, Vy – проекции вектора скорости на ось y:
При t 1 = 1c имеем:
Определяем модуль вектора скорости:
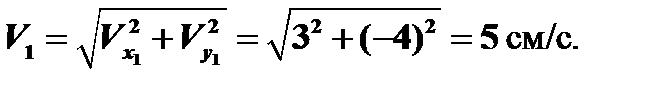
Вектор скорости строим в масштабе (1 см ‒ 2 см/с) по его проекциям.
3. Определяем ускорение точки.
При координатном способе задания движения вектор ускорения точки определяется:
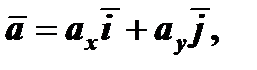
где аx – проекция вектора ускорения на ось х, ау – проекция вектора ускорения на ось у:
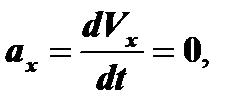
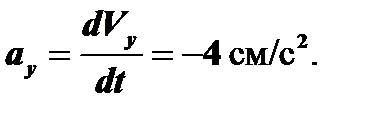
Определяем модуль вектора ускорения:
Строим в масштабе (1 см ‒ 1 см/с2) вектор ускорения по его проекциям, параллельным координатным осям.
4. Определяем касательное и нормальное ускорения.
Величину касательного ускорения находим по формуле:
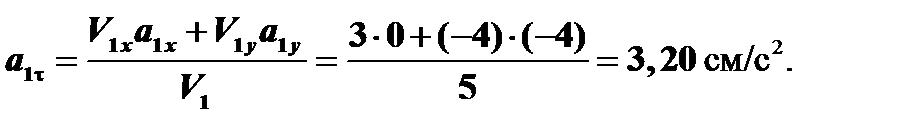
Величину нормального ускорения находим по формуле:
5. Определяем радиус кривизны траектории: 
| x |
| y |
| n |
| t |
|
|
|
|
|
|
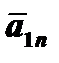
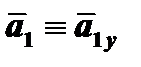
| М 1(4;1) |
| М 0 |
|
|
|
Результаты вычислений сведены в таблицу.
| Координаты, см | Скорость точки, см/с | Ускорение точки, см/с2 | Радиус кривизны, см | |||||||
| x 1 | y 1 |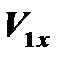 
| 
| 
| 
| 
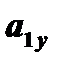
| a 1 |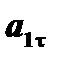 
| 
| r 1 |
| -4 | -4 | 3,20 | 2,40 | 10,42 |
Задание K-2. Исследование сложного движения
Материальной точки
Тело (квадрат со стороной 10 см или диск радиусом R = 5 см) вращается вокруг неподвижной оси по закону jе = f 1(t). По желобу, имеющему прямолинейную форму или форму дуги окружности, движется материальная точка М по закону ОМ = Sr = f 2(t).
На рисунках точка М показана в положении, при котором Sr > 0; положительное направление отсчета угла jе указано дуговой стрелкой.
Найти абсолютные скорость и ускорение точки М для заданного момента времени t = t 1.
Дано: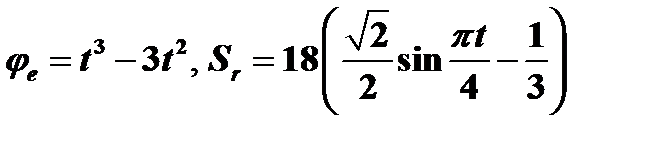 
(j ‒ рад, S ‒ см, t ‒ с), l = 0, b = 10 см, t 1 = 1 c, АО = ОВ.
Определить: абсолютную скорость 
и абсолютное ускорение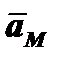 
точки М.
| А |
| B |
| l |
| O |
| (+) |
| (‒) |
| jе |
| M |
Решение.
1. Точка М совершает сложное движение: относительное движение по поверхности пластины и переносное ‒ вращение вместе с пластиной вокруг неподвижной оси.
Абсолютную скорость точки находим по теореме о сложении скоростей при сложном движении точки:
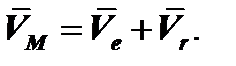
Для этого определим относительную и переносную скорости точки М в момент времени t 1 = 1 c по модулю и направлению.
2. Рассмотрим относительное движение точки, заданное естественным способом. Найдем положение точки М на траектории относительного движения (прямая АВ) в заданный момент времени:
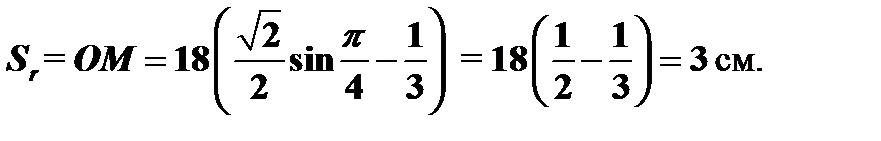
Точка в заданный момент времени находится в положительном направлении отсчета координаты S относительно т. О.
Определяем относительную скорость:
при t = 1 c
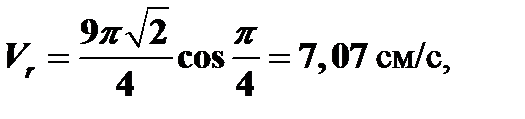
направлен вектор в сторону положительных значений координаты S относительно начала отсчета О.
3. Определяем переносную скорость:
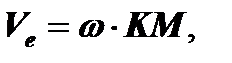
где 
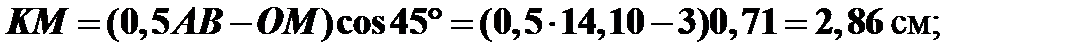
следовательно: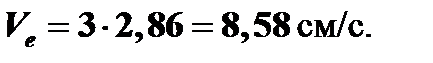 
Вектор переносной скорости точки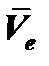 
направлен перпендикулярно плоскости рисунка в сторону вращения пластины(
).
|
|
|
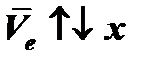| «е» |
| KR |
|
| А |
| О 1 |
| x |
| y |
| z |
| wе |
| b |
| В |
|
|
|
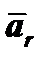
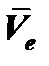
| М |
| O |
| (+) |
| (‒) |
| jе |
|
| «r» |
|
| 45° |
Так как вектор относительной скорости лежит в плоскости yz, а вектор переносной скорости параллелен оси x, то модуль абсолютной скорости определяем по теореме Пифагора:
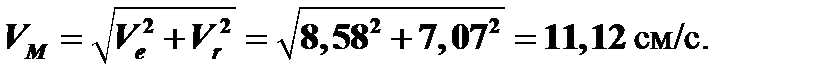
3. Абсолютное ускорение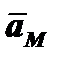 
точки М определяется по теореме Кориолиса:
или, учитывая, что траектория переносного движения точки окружность и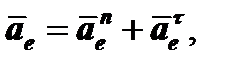 
получим:
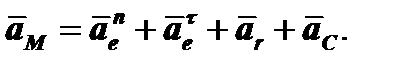(1)
Так как траекторией относительного движения является прямая линия, то:
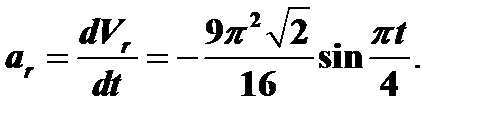
при t = 1 c
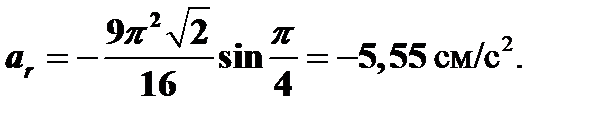
Направлен вектор относительного ускорения в сторону отрицательных значений относительно начала отсчета О.
Определяем нормальное и касательное ускорения точки в переносном движении:
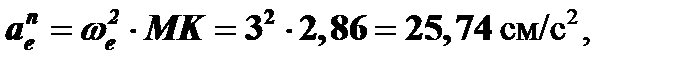
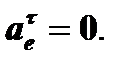
Вектор переносного нормального ускорения точки 
направлен по радиусу МК к оси переносного вращения.
Вычислим модуль ускорения Кориолиса:
Направление ускорения Кориолиса определяем по правилу Жуковского: вектор относительной скорости 
проецируем на плоскость, перпендикулярную оси переносного вращения и поворачиваем проекцию в этой плоскости в сторону переносного вращения на угол 90° (
).
Для определения модуля абсолютного ускорения спроецируем обе части векторного равенства (1) на оси декартовой системы координат:
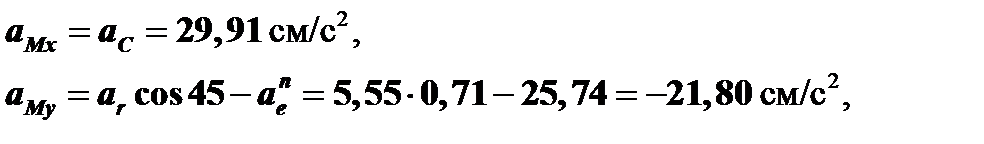
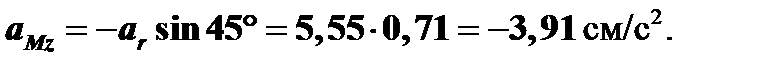
Вычисляем модуль абсолютного ускорения точки М по формуле:
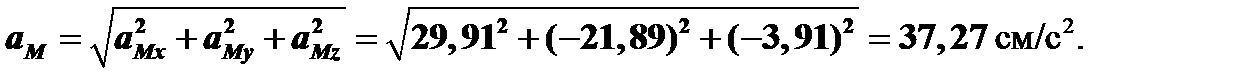
Ответ: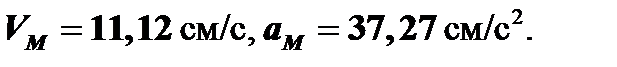 
|
|
|
