 |
Цепь Маркова для восстанавливаемого элемента систем электроснабжения без преднамеренных отключений
|
|
|
|
Рассмотрим простейший случай, когда плановые ремонты или любые другие преднамеренные отключения отсутствуют. Элемент СЭС находится в эксплуатации до тех пор, пока не откажет. После отказа выполняется его аварийный ремонт, и элемент снова поступает в эксплуатацию.
Такая упрощенная математическая модель не является чистой абстракцией и соответствует стратегии обслуживания с аварийными ремонтами. По стратегии аварийных ремонтов эксплуатируется практически вся бытовая техника, ряд мало ответственных промышленных потребителей, сельского хозяйства и других отраслей народного хозяйства. Более того, при низком значении ущерба от отказа стратегия аварийных ремонтов является оптимальной с точки зрения минимума средних удельных затрат на ремонт и восстановление [2]. Даже при наличии профилактического обслуживания, его в ряде случаев можно не учитывать. На промышленных предприятиях профилактические ремонты элементов СЭС часто выполняются в выходные или праздничные дни, совместно с ремонтом технологического оборудования, не оказывают влияния на производственный процесс и не ведут к ущербам.
Элемент СЭС без преднамеренных отключений будет иметь лишь два состояния: 0 – работоспособное; 1 – состояние аварийного восстановления. Цепь Маркова для такого элемента может быть изображена в виде направленного графа (рис.2.2), у которого вершины изображают соответствующие состояния элемента, а ребра – события переходов, отказов или восстановлений.

Рис.2.2. Цепь Маркова для элемента без преднамеренных отключений
Пусть в момент времени 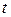 элемент находится в работоспособном состоянии с вероятностью
элемент находится в работоспособном состоянии с вероятностью  . Условная вероятность того, что за время
. Условная вероятность того, что за время  не произойдет отказа и элемент останется в работоспособном состоянии равна
не произойдет отказа и элемент останется в работоспособном состоянии равна
|
|
|
 . .
|
Безусловная вероятность того, что на интервале времени  отказа не произойдет, равна произведению
отказа не произойдет, равна произведению  . С другой стороны в момент времени
. С другой стороны в момент времени 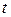 с вероятностью
с вероятностью  элемент мог находиться в состоянии аварийного ремонта. За время
элемент мог находиться в состоянии аварийного ремонта. За время  ремонт может завершиться с вероятностью
ремонт может завершиться с вероятностью  . А вероятность перехода элемента из состояния 1 в состояние 0 равна произведению
. А вероятность перехода элемента из состояния 1 в состояние 0 равна произведению  .
.
Таким образом, к моменту времени  элемент либо останется в состоянии 0, либо перейдет из состояния 1 в состояние 0, а вероятность
элемент либо останется в состоянии 0, либо перейдет из состояния 1 в состояние 0, а вероятность  будет равна сумме
будет равна сумме
 .
.
Раскрывая скобки, получим дифференциальное уравнение относительно вероятности пребывания элемента в работоспособном состоянии:
 . .
| (2.12) |
Аналогично для состояния аварийного ремонта получим:
 . .
| (2.13) |
Уравнения (2.12), (2.13) представляют собой систему дифференциальных уравнений относительно вероятностей  . Их решение зависит от начальных условий.
. Их решение зависит от начальных условий.
Естественно принять, что в начале срока эксплуатации элемент полностью работоспособен, то есть  . Для указанных начальных условий решение системы уравнений (2.12), (2.13) может быть записано в виде:
. Для указанных начальных условий решение системы уравнений (2.12), (2.13) может быть записано в виде:
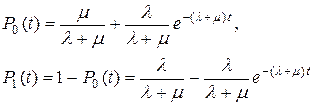 . .
| (2.14) |
Вероятность застать элемент в работоспособном состоянии определяет его коэффициент готовности  . Коэффициент аварийного простоя, как вероятность застать элемент в произвольный момент времени
. Коэффициент аварийного простоя, как вероятность застать элемент в произвольный момент времени 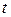 в неработоспособном состоянии, равен
в неработоспособном состоянии, равен  .
.
Задача 2.3.
Схема расчета надежности резервированного устройства для различных вариантов приведена на рис. 2.3 а-г. Интенсивности отказов элементов имеют следующие значения:
 1/ч;
1/ч;  1/ч;
1/ч;  1/ч;
1/ч; 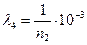 1/ч,
1/ч,
где  – последняя цифра учебного шифра (цифра 0 соответствует
– последняя цифра учебного шифра (цифра 0 соответствует 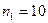 );
);  – предпоследняя цифра учебного шифра (цифра 0 соответствует
– предпоследняя цифра учебного шифра (цифра 0 соответствует  ). Предполагается, что последействие отказов элементов отсутствует. Необходимо найти среднюю наработку до первого отказа устройства и вероятность его безотказной работы в течение 100 часов.
). Предполагается, что последействие отказов элементов отсутствует. Необходимо найти среднюю наработку до первого отказа устройства и вероятность его безотказной работы в течение 100 часов.
|
|
|
Типовой пример. Схема расчета надежности резервированного устройства приведена на рис. 2.4. Интенсивности отказов элементов имеют следующие значения:
 1/ч;
1/ч;  1/ч;
1/ч;  1/ч. Предполагаем, что последействие отказов элементов отсутствует. Необходимо найти среднюю наработку до первого отказа устройства.
1/ч. Предполагаем, что последействие отказов элементов отсутствует. Необходимо найти среднюю наработку до первого отказа устройства.
Решение. Готовой формулы для средней наработки до первого отказа в рассматриваемом случае нет. Поэтому необходимо воспользоваться соотношением
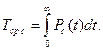
Найдем выражение для вероятности безотказной работы 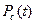 устройства. Очевидно,
устройства. Очевидно, 
где

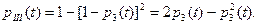
Тогда, подставляя значения  и
и  в выражение для
в выражение для 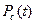 , получим
, получим

Так как  ,
,  ,
,  , то
, то


Подставляя в выражение для  значение интенсивности отказов из условия задачи, получаем
значение интенсивности отказов из условия задачи, получаем

 ч.
ч.
Задача 2.4.
Составить систему уравнений Колмогорова для графа состояний резервированной системы, изображенного на рис. 2.5, а-г (в соответствии с вариантом). В данном случае  и
и 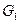 – неработоспособное состояние;
– неработоспособное состояние;  – вероятность нахождения системы в i-ом состоянии;
– вероятность нахождения системы в i-ом состоянии;  – интенсивность отказа;
– интенсивность отказа;  – интенсивность восстановления. Рассчитать коэффициент готовности системы
– интенсивность восстановления. Рассчитать коэффициент готовности системы  решив полученную систему уравнений.
решив полученную систему уравнений.
 1/ч;
1/ч;  1/ч.
1/ч.
Нерезервированная восстанавливаемая система в произвольный момент времени находится в одном из двух состояний: работоспособном  или неработоспособном
или неработоспособном  . Процесс её функционирования можно отразить графом состояний (рис. 2.2):
. Процесс её функционирования можно отразить графом состояний (рис. 2.2):
Из состояния  в состояние
в состояние 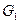 система переходит в результате отказов с интенсивностью
система переходит в результате отказов с интенсивностью  , а из
, а из 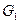 в
в  – в результате восстановления с интенсивностью
– в результате восстановления с интенсивностью  . В дальнейшем будем считать, что потоки отказов и восстановлений являются простейшими:
. В дальнейшем будем считать, что потоки отказов и восстановлений являются простейшими: 
 Это значит, что производительность труда ремонтника постоянна и не зависит от времени. Поэтому время восстановления имеет экспоненциальный закон распределения
Это значит, что производительность труда ремонтника постоянна и не зависит от времени. Поэтому время восстановления имеет экспоненциальный закон распределения 

Процесс функционирования резервированной восстанавливаемой системы является Марковским случайным процессом с дискретными состояниями. Случайный процесс называется дискретным, если его состояние можно пронумеровать и переход из состояния в состояние происходит скачком. Резервированная восстанавливаемая система описывается графом состояний (рис. 2.6).
|
|
|
В отличие от нерезервированной системы резервированная система в общем случае имеет три состояния:  – исправное,
– исправное, 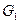 – неисправное, но работоспособное,
– неисправное, но работоспособное,  – неработоспособное.
– неработоспособное.
Переход системы из состояния в состояние происходит под воздействием потоков отказов и восстановлений. Если все потоки событий, переводящие систему из состояния в состояние, являются пуассоновскими, то случайный процесс есть Марковский процесс и задается системой дифференциальных уравнений.
Система составляется по следующим правилам. Производная вероятности состояния равна сумме стольких слагаемых, сколько стрелок связано с этим состоянием. Каждое слагаемое равно произведению интенсивности потока событий, переводящего систему по данной стрелке, на вероятность того состояния, из которого исходит стрелка. Слагаемое имеет знак минус, если стрелка исходит из данного состояния, а знак плюс – если стрелка направлена в данное состояние. Полученная система уравнений называется системой уравнений Колмогорова.
Например, для графа состояний, показанного на рис.2.7, получим следующую систему дифференциальных уравнений.
 . .
| (2.15) |
Система решается с помощью преобразований Лапласа или численными методами. При  справедлива предельная теорема А.А. Маркова: если все интенсивности потоков событий постоянны, а граф состояний таков, что из каждого состояния можно перейти в каждое другое за конечное число шагов, то предельные вероятности состояний существуют и не зависят от начального состояния системы. В соответствии с этой теоремой при
справедлива предельная теорема А.А. Маркова: если все интенсивности потоков событий постоянны, а граф состояний таков, что из каждого состояния можно перейти в каждое другое за конечное число шагов, то предельные вероятности состояний существуют и не зависят от начального состояния системы. В соответствии с этой теоремой при  производная
производная  и система дифференциальных уравнений превращается в однородную систему линейных алгебраических уравнений
и система дифференциальных уравнений превращается в однородную систему линейных алгебраических уравнений
 . .
| (2.16) |
Система дополняется нормировочным уравнением
 . .
| (2.17) |
|
|
|


