 |
Синтез реактивных двухполюсников
|
|
|
|
Введение
Задача высшего специального образования – научить студента разби-раться в большом объеме разнообразной технической информации.
Одной из основных общеинженерных дисциплин для инженеров-электриков любой специализации является «Теория линейных электрических цепей» (ТЛЭЦ). Курс ТЛЭЦ дает знания, необходимые для изучения специальных курсов. Линейные электрические цепи – это электрические системы, которые входят в состав любых устройств автоматики и электросвязи. Некоторые устройства, содержащие, например, электронные приборы, нельзя считать линейными электрическими цепями, но в определенном режиме работы такие устройства имеют свойства электрических цепей, и анализ их работы производится на основе ТЛЭЦ. В курсе ТЛЭЦ изучаются методы расчета электрических устройств, которые являются общими для линейных цепей и любых электрических систем.
Без знания ТЛЭЦ невозможно совершенствовать и разрабатывать новые системы электросвязи и автоматики, микропроцессорной техники, нельзя обеспечить грамотное техническое обслуживание эксплуатационного обо-рудования.
Выполнение курсовой работы по ТЛЭЦ способствует закреплению теоретических знаний по основным разделам курса – «Двухполюсники» и «Четырехполюсники» – и получению практических навыков, необходимых при эксплуатации, проектировании, разработке и усовершенствовании устройств автоматики, телемеханики и связи.
Общие положения
При проектировании современных устройств автоматики, телемеханики и связи решаются многочисленные задачи, связанные с использованием электрических явлений для передачи и обработки информации. В общем случае электрическая цепь состоит из источников электрической энергии, приемников и промежуточных звеньев, связывающих источники с приемниками. При выполнении курсовой работы необходимо произвести анализ и синтез основных промежуточных элементов: двух- (ДП) и четырехполюсников (ЧП).
|
|
|
Задача анализа электрической цепи – определение реакции цепи y (t), y (ω) на заданное внешнее воздействие х (t), х (ω). Задача синтеза – нахождение цепи по заданной ее реакции y (t), y (ω) на заданное внешнее воздействие х (t), х (ω).
Исходными данными в задаче анализа являются эквивалентная схема ДП (ЧП) и значения параметров всех входящих в нее элементов; описание внешнего воздействия.
В результате анализа определяется отклик (реакция) цепи в виде совокупности токов и напряжений. В зависимости от того, какая величина – частота или время – является аргументом в выражениях, описывающих соотношения между откликом и внешним воздействием, различают частотные и временные характеристики цепи.
Исходные данные в задаче синтеза: описание внешнего воздействия х (ω) и его отклика y (ω).
В задаче синтеза необходимо определить эквивалентную схему цепи и значения параметров всех входящих в нее элементов.
Анализ и синтез электрических цепей взаимосвязаны. Методы синтеза базируются на использовании общих свойств характеристик различных классов цепей, которые изучаются в процессе анализа.
В задании к курсовой работе приводится схема синтезируемого ЧП, составными частями которого являются ДП с известной частотной зависимостью сопротивления в символической или операторной форме.
В электрической цепи с сосредоточенными параметрами типа R, L, C (рис. 1.1) уравнение равновесия напряжения с подключенным внешним источником имеет вид:
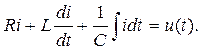 (1.1)
(1.1)
При изображении установившихся гармонических напряжения и тока функцией еjωt интегродифференциальное уравнение равновесия напряжения
|
|
|
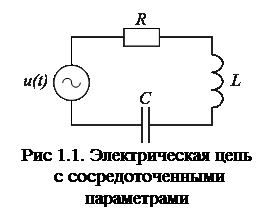 (тока) (1.1) превращается в алгебраическое. То же самое упрощение получается, когда зависимости u (t) и i (t) от времени отображаются функцией еpt, где р – любое комплексное число. Тогда
(тока) (1.1) превращается в алгебраическое. То же самое упрощение получается, когда зависимости u (t) и i (t) от времени отображаются функцией еpt, где р – любое комплексное число. Тогда
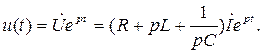 (1.2)
(1.2)
Отсюда 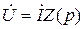 или
или 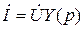 , где
, где 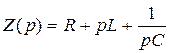 – операторное сопротивление;
– операторное сопротивление; 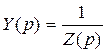 – опе-раторная проводимость ДП.
– опе-раторная проводимость ДП.
Для реактивных ДП комплексное число р может быть заменено на jω (р = jω) и операторные характеристики совпадают с частотными. Таким образом, при решении задач курсовой работы можно воспользоваться символическим или операторным методом.
Синтез реактивных двухполюсников
Функция Z (p) или Y (p), по которой можно построить соответствующую электрическую цепь, называется физически реализуемой. Удобнее всего представить исследуемый ДП в виде одной из четырех канонических схем. Реализуемая функция сопротивления (проводимости) должна иметь вид рациональной дроби:
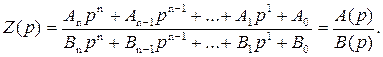 (2.1)
(2.1)
Многочлены в числителе и знаменателе рациональной дроби удобнее всего представить в виде произведения множителей вида (p – p i), где p i – корни многочленов А (р) и В (р):
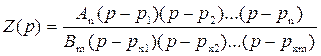 . (2.2)
. (2.2)
Значения переменного р, соответствующие корням многочлена А (р), обращают функцию Z (p) в нуль и называются нулями функции Z (p). При значениях р, соответствующих корням многочлена В (р), функция Z (p) становится неограниченно большой. Корни многочлена В (р) являются полюсами функции операторного сопротивления Z (p). Нули и полюсы физически реализуемой функции Z (p) всегда чередуются.
Определим нули и полюсы функции Z (p) ДП и построим полюсно-нулевое изображение на плоскости комплексного переменного.
При построении схемы ДП по заданному (ым) значению (ям) оператор-ного сопротивления Z (p) требуется выполнить следующие этапы синтеза:
1) выявить необходимые и достаточные условия, которым должна удов-летворять функция Z (p) для того, чтобы существовала хотя бы одна реали-зуемая цепь;
2) если функция Z (p) задана графиком (таблицей), то необходимо по-добрать рациональную функцию, наиболее точно воспроизводящую все свойства ДП, заданные графиком;
3) рассчитать все канонические схемы ДП, удовлетворяющие заданному выражению;
4) выбрать оптимальную из рассчитанных цепей для практического использования, имея в виду, что большие значения индуктивности элементов схем ДП нежелательны при реализации. Для этого все заданные формулы функции Z (p) проверяют на следующие необходимые и достаточные условия:
|
|
|
функция Z (p) реализуема, если она положительна и действительна, все коэффициенты при операторе р – только вещественные и положительные числа;
высшие и низшие степени многочленов числителя и знаменателя функции Z (p) отличаются не более чем на единицу;
нули и полюсы функции Z (p) пассивных ДП расположены в левой полуплоскости комплексного переменного. При этом мнимые корни бывают комплексно-сопряженными, нули и полюсы чередуются, отсутствуют кратные (одинаковые) корни;
если корни (нули и полюсы) функции Z (p) расположены на мнимой оси, то такая функция соответствует реактивному ДП. При этом в числителе (знаменателе) функции оператор р имеет только четные степени, а в знаменателе (числителе) – только нечетные. Разница между высшими и низшими степенями оператора р у числителя и знаменателя равна единице. Высшая степень оператора р равна числу реактивных элементов в канонической схеме.
Синтез пассивных ДП осуществляется двумя методами разложения:
на простые дроби, в результате чего при условии физической реализуемости получают канонические схемы Фостера первого или второго рода;
в непрерывные (цепные) дроби, при этом получаются канонические схемы Кауэра первого или второго рода (лестничные схемы).
Наиболее распространен первый метод разложения. При выделении простых слагаемых из функции Z (p) получают последовательное соединение двухэлементных резонансных контуров (схему Фостера первого рода).
При разложении функции Y (p) на простые слагаемые реализуется схема Фостера второго рода (параллельное соединение простых LC -элементов).
Для самого общего случая реактивного ДП класса «∞ – ∞» (рис. 2.1) функция сопротивления имеет вид:
 , (2.3)
, (2.3)
| где | 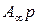 – целая часть дроби (полюс при р = ∞); – целая часть дроби (полюс при р = ∞);
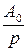 – полюс при р = 0; – полюс при р = 0;
 – пары мнимых полюсов функции при р = ± jω 2i. – пары мнимых полюсов функции при р = ± jω 2i.
|
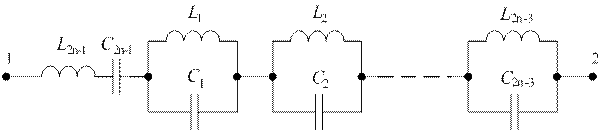
Рис. 2.1. Схема двухполюсника класса «∞ – ∞» (общий случай)
|
|
|
Значения коэффициентов А∞, А 0, А i в функции (2.3) определяются методом разложения:
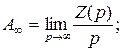 (2.4)
(2.4)
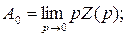 (2.5)
(2.5)
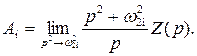 (2.6)
(2.6)
Учитывая, что 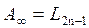 ,
, 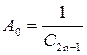 и
и  , а также
, а также 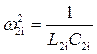 , можно определить элементы
, можно определить элементы 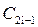 ,
, 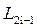 ,
, 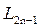 ,
, 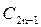 схемы.
схемы.
В качестве примера определим элементы схемы, сопротивление которой задано рациональной дробью в операторной форме:
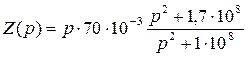 . (2.7)
. (2.7)
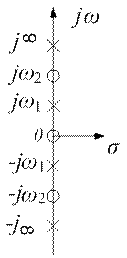
Выявляем необходимые и достаточные условия физической реализации схемы ДП. Строим полюсно-нулевое изображение (рис. 2.2, а) и характеристи-ческую строку (рис. 2.2, б). По ним определяем класс ДП, количество резо-нансов, элементов и вид схемы.
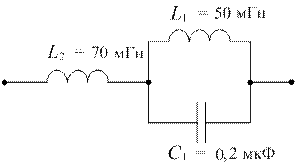
Допустим, выбрали схему Фостера первого рода, состоящую их трех элементов (высшая степень оператора р – третья). Так как класс ДП «0 – ∞» (это видно из полюсно-нулевого изображения функции Z (p)), то схема примет вид, изображенный на рис. 2.2, в.
Тогда из уравнений (2.4) – (2.6) функция
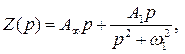 (2.8)
(2.8)
где  ;
; 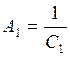 ;
;  .
.
Используя уравнения (2.4) – (2.6), получим:
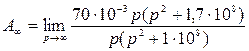 ; (2.9)
; (2.9)
 ;
;
 ; (2.10)
; (2.10)
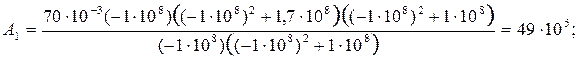
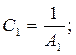 (2.11)
(2.11)
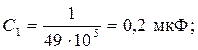
|
 б
б
|
| а | |
| 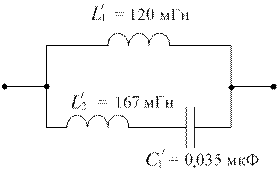
|
| в | г |

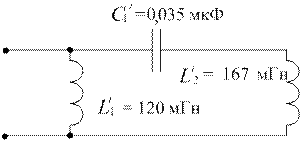
| 
|
| д | е |
Рис. 2.2. Синтез реактивных двухполюсников:
а – полюсно-нулевое изображение функции Z (p); б – характеристическая строка; в – схема Фостера первого рода; г – схема Фостера второго рода; д – схема Кауэра первого рода; е – схема Кауэра второго рода
 ; (2.12)
; (2.12)
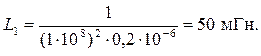
Если использовать функцию 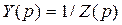 , то в результате разложения на простые дроби получим схему Фостера второго рода (рис. 2.2, г) того же класса («0 – ∞»).
, то в результате разложения на простые дроби получим схему Фостера второго рода (рис. 2.2, г) того же класса («0 – ∞»).
При разложении в непрерывную дробь функции Z (p) по нисходящим степеням оператора р получим значения элементов схемы Кауэра первого рода (рис. 2.2, д):
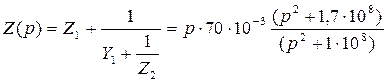 ; (2.13)
; (2.13)

| (2.14) |
При разложении в непрерывную дробь функции Y (p) по восходящей степени оператора р получим значения элементов схемы Кауэра второго рода (рис. 2.2, е):
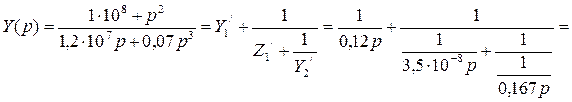
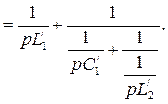 (2.15)
(2.15)
Для трехэлементных ДП схемы Фостера и Кауэра одинаковы, однако для более сложных ДП они будут различными. При сравнении схем, приведенных на рис. 2.2, видно, что в схеме рис. 2.2, г значения индуктивности больше, чем в схеме рис. 2.2, в, хотя количество катушек индуктивности одинаковое. Для физической реализации более целесообразно использовать схему ДП, изобра-женную на рис. 2.2, в.
Таким образом, при выполнении курсовой работы на первом этапе требуется
1) выявить необходимые и достаточные условия физической реализуемос-ти всех ДП, заданных функцией Z (p) или Y (p) в исходных данных;
2) определить все возможные схемы ДП, используя методы разложения на простые дроби и в непрерывные цепные дроби;
3) выбрать оптимальную схему ДП и использовать ее в дальнейшем при расчетах;
4) построить графики частотной зависимости сопротивления ДП.
|
|
|
При построении графика необходимо задаваться двумя – тремя значениями частоты в диапазонах между конечными и резонансными частотами ДП. Например, для ДП (см. рис. 2.2, в) резонансные частоты 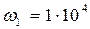 с–1 и
с–1 и 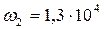 с–1. Результаты расчета сопротивления Z (p) сведены в табл. 2.1, а график функции Z (p) приведен на рис. 2.3.
с–1. Результаты расчета сопротивления Z (p) сведены в табл. 2.1, а график функции Z (p) приведен на рис. 2.3.
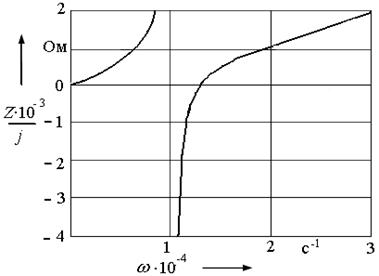
Рис. 2.3. Частотная зависимость сопротивления двухполюсника
Таблица 2.1
Расчет сопротивления Z (p)
| Параметр | Значение параметра | |||||||||
| ω ∙10-4, с-1 | 0,2 | 0,4 | 1,0 | 1,1 | 1,2 | 1,3 | 1,5 | 2,0 | ∞ | |
| Z, Ом | j 232 | j 513 | ∞ | – j 1797 | – j 496 | j 462 | j 1073 | ∞ |
|
|
|


