 |
Эквивалентность четырехполюсников
|
|
|
|
При расчете электрических схем бывают случаи, когда в схеме можно изменить число входящих в нее элементов. При этом сохраняются все электрические свойства схемы, хотя структура и входящие в нее элементы полностью изменяются.
Условием эквивалентности ЧП является равенство их собственных параметров, например (А (1)) = (А (2)), параметров х. х. и к. з., а также рабочих передаточных функций Н (р).
В курсовой работе задается вид схемы замещения синтезируемого ЧП. Необходимо рассчитать элементы эквивалентного пассивного ЧП, используя условие равенства соответствующих А -параметров исходного и эквивалентного четырехполюсников. Матрицы А -параметров схем замещения наиболее часто применяемых ЧП приведены в работах [1, 2].
Мостовая несимметричная схема ЧП – наиболее общий случай, она эквивалентна всем другим схемам ЧП, но содержит большое количество элементов и может быть представлена в виде какого-либо соединения более простых элементов с использованием идеального трансформатора.
В случае пассивных ЧП практическое применение имеет замена многоэлементных симметричных ЧП эквивалентными Т-, П-образными схемами и схемами, содержащими идеальный трансформатор (рис. 4.1).
Если представить мостовой ЧП в виде последовательного или параллельного соединения двух и более простых ЧП с включением реального трансформатора, имеющего малые потери и коэффициент трансформации, близкий к единице (например, n = 0,999), то можно получить эквивалентные симметричному мосту схемы со значительно меньшим числом элементов (см. рис. 4.1).
Активные RC -фильтры (АRСФ) чаще всего применяются на низких частотах, когда катушки индуктивности неприемлемы из-за громоздкости и плохого качества.
|
|
|
|
| 
|
| а | б | в |
Рис. 4.1. Схемы, эквивалентные симметричному мосту
Наиболее широко используются следующие основные методы реали-зации АRСФ:
1) имитации индуктивности;
2) нормирования по переменному сопротивлению;
3) переменных состояний;
4) каскадная.
Каскадная реализация позволяет минимизировать число операционных усилителей (ОУ) и удобна для настройки элементов после расчета, так как каждое звено изолировано от других высоким входным и низким выходным сопротивлениями ОУ.
Разработка фильтра начинается с определения передаточной функции Н (р), ее нулей и полюсов. В общем случае передаточная функция имеет вид:
. (4.1)
При m ≤ n выражение (4.1) можно представить в виде произведения:
, (4.2)
где k ≤ n,
, (4.3)
– коэффициенты, рассчитанные для соответствующих системных функций по формулам, приведенным в табл. 4.1.
Для каждого значения i = 1, 2,..., k функция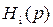 
является либо передаточной функцией звена первого порядка (4.4), либо передаточной функцией звена второго порядка (биквадом) (4.5):
; (4.4)
. (4.5)
Числитель (знаменатель) формулы (4.4) получается из вещественного корня полинома числителя (знаменателя) формулы (4.1), а числитель (знаменатель) выражения (4.5) – из пары комплексно сопряженных корней. Если в выражениях (4.4), (4.5) 
, то 
– передаточная функция ФНЧ, если 
– ФВЧ, если 
– ППФ, если 
– ПЗФ.
Расчетные формулы элементов соответствующих фильтров с одним операционным усилителем приведены в табл. 4.1.
Если в результате реализации биквадов, полученных из формулы (4.1), остается коэффициент G < 1,то на входе или выходе схемы включают дополнительный ЧП, схема которого приведена на рис. 4.2. При включении дополнительного ЧП на входе схемы его элементы определяются из следующего соотношения с учетом того, что 
:
, (4.6)
а при включении на выходе –
. (4.7)
Одно из сопротивлений (R 1 или R 2) задается, а второе – вычисляется по формуле (4.6) или (4.7).
|
|
|
Если коэффициент G < 0, то целесообразно включить делитель в цепь обратной связи инвертирующего операционного усилителя (рис. 4.3). При этом элементы делителя определяются из выражения:
. (4.8)
| 
|
| Рис. 4.2. Схема делителя при G < 1 | Рис. 4.3. Схема делителя при G < 0 |
|
|
|
