 |
Теорема о замене подформул на эквивалентные
|
|
|
|
Пусть N Î< M > и имеет вид: N (x 1,..., xn) = g (G 1,... Gi,..., Gm). Пусть подформула Gi ~ Gi ¢, тогда формула N (x 1,..., xn) = g (G 1,..., Gi,..., Gm) эквивалентна формуле N ¢(x1,..., xn) = g (G 1¢,..., Gi ¢,..., G ¢ m).
Доказательство. Формулы N и N ¢ эквивалентны, если реализуют одну и ту же функцию. Согласно построению функции, реализующей формулу имеем:
N (x 1,..., xn) = g (f 1(x 1,..., xn),..., fi (x 1,..., xn),..., fm (x 1,..., xn)),
N ¢ (x 1,..., xn)= g (f 1¢ (x 1,..., xn),..., fi ¢(x 1,..., xn),..., fm ¢ (x 1,..., xn)).
По условию Gi ~ Gi ¢, следовательно на наборе (a 1,..., an) имеем fi (a 1,..., an) = = fi ¢(a 1,..., an) следовательно, на любом наборе (a 1,..., an)значения функции g (f 1,..., fi,..., fm) и g (f 1¢,..., fi ¢,..., fm ¢) совпадают. Получим N ~ N ¢.
Некоторые свойства элементарных функций
1. Идемпотентность & и Ú: х & x = x, x Ú x = x.
2. Коммутативность &,Ú,Å,|,~,  .
.
3. Ассоциативность &,Ú,Å,~, поэтому в формулах вида xyz можно не ставить никаких скобок.
4. Дистрибутивность:
а) & по отношению к Ú: x &(y Ú z)= xy Ú xz,
б) Ú по отношению к &: x Ú(y & z)=(x Ú y)&(x Ú z),
в) & по отношению к Å: x (y Å z)= xy Å xz.
5. Инволюция:  = х.
= х.
6. Правило де Моргана: 
 =
=  &
& 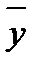 и
и  =
= 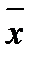 Ú
Ú  .
.
7. Законы действия с 0 и 1:
x Ú0= x, x Ú1=1, x Ú  =1, x &0=0, x &1= x, x &
=1, x &0=0, x &1= x, x &  =0, x Å1=
=0, x Å1=  , x Å0= x.
, x Å0= x.
8. Самодистрибутивность импликации: x  (y
(y  z)=(x
z)=(x  y)
y)  (x
(x  z).
z).
Равенство всех этих формул доказывается по определению, т.е. по равенству функций, которые они реализуют.
Проверим для примера самодистрибутивность импликации: x  (y
(y  z)=(x
z)=(x  y)
y)  (x
(x  z).
z).
| x | y | z | y  z z
| x  (y (y  z) z)
| x  y y
| x  z z
| 
|
Принцип двойственности
Определение 1. Функции f *(x 1,..., xn) называется двойственной к функции f (x 1,..., xn), если f *(x 1,..., xn) =  (
( 1,...,
1,...,  n).
n).
Пример 1. Покажем с помощью таблицы истинности, что константа 0 двойственна к 1:
|
|
|
| x | f | f * |
Функции f (x) = x и g (x) =  двойственны сами себе:
двойственны сами себе:
| x | f | f * | g | g * |
так как f *(0)= 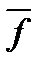 (1).
(1).
Определение 2. Если f *(x 1,..., xn) = f (x 1,..., xn), то f (x 1,..., xn) называется самодвойственной.
Пример 2. Покажем, что f (x 1, x 2, x 3)= x 1Å x 2Å x 3 – самодвойственна:
| x 1 | x 2 | x 3 | f | f * |
Если f *– самодвойственна, то  (
( 1,...,
1,...,  n) = f (x 1,..., xn), т.е. на противоположных наборах функция принимает противоположные значения.
n) = f (x 1,..., xn), т.е. на противоположных наборах функция принимает противоположные значения.
Пример 3. Покажем, что функция х 1Ú х 2 двойственна к x 1& x 2, функция х 1  х 2 двойственна к функции x 1| x 2.
х 2 двойственна к функции x 1| x 2.
| x 1 x 2 | f = х 1Ú х 2 | f * | g = x 1| x 2 | g *= x 1  x 2 x 2
|
| 0 0 0 1 1 0 1 1 |
Теорема о двойственных функциях
Если f * двойственна к f, то f двойственна к f *.
Доказательство. f *(x 1,..., xn) =  (
(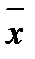 1,...,
1,..., 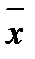 n). Найдем двойственную функцию к f *, т.е. (f *(x 1,..., xn))* = (
n). Найдем двойственную функцию к f *, т.е. (f *(x 1,..., xn))* = (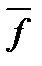 (
( 1,...,
1,...,  n))* =
n))* =  (
( 1,...,
1,..., 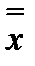 n) = f (x 1,.., xn).
n) = f (x 1,.., xn).
Предположим, что функция задана формулой. Можно ли найти по этой формуле двойственную функцию? Ответ на этот вопрос дает следующая теорема.
Принцип двойственности
Теорема: Пусть функция h (x 1,..., xn) реализована формулой h (x 1,..., xn) = = g (G 1,..., Gm) = g (f 1(x 1,..., xn),..., fm (x 1,..., xn)), где какие-то переменные могут быть фиктивными. Тогда h *(x 1,..., xn) = g *(f 1*(x 1,..., xn),..., fm *(x 1, …, xn)), это означает, что если функция задана некоторой формулой, то чтобы получить двойственную функцию, надо в этой формуле все знаки функций заменить на двойственные, 0 на 1, 1 на 0.
Доказательство. h *(x 1,..., xn) =  (
( 1,...,
1,...,  n) =
n) =  (f 1(
(f 1( 1,...,
1,...,  n),..., fm (
n),..., fm ( 1,...,
1,...,  n)) =
n)) =  (
( 1(
1( 1,...,
1,...,  n),...,
n),..., 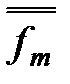 (
( 1,...,
1,...,  n)) = g ((
n)) = g (( ),..., ((
),..., (( ) = g *(f 1*(x 1,..., xn),..., fm *(x 1,..., xn)), что и требовалось доказать.
) = g *(f 1*(x 1,..., xn),..., fm *(x 1,..., xn)), что и требовалось доказать.
Если функция h (x 1,..., xn) реализуется формулой N [ f 1,..., fn ], то формулу, полученную из N заменой fi, входящих в нее, на fi * и реализующую функцию h *(x 1,..., xn), будем называть двойственной и обозначать N *(x 1,..., xn).
Пример 4. Построить формулу, реализующую f *, если f = ((x  y) Ú z) (y
y) Ú z) (y 
 (x Å yz)). Покажем, что она эквивалентна формуле N = z (x Å y).
(x Å yz)). Покажем, что она эквивалентна формуле N = z (x Å y).
|
|
|
Найдем (x Å y)* и (x  y)*.
y)*.
| x y | x Å y | (x Å y)* | x  y y
| (x  y)* y)*
|
| 0 0 0 1 1 0 1 1 |
Из таблиц видно, что
(x  y)* = x ~ y =
y)* = x ~ y =  = x
= x  y
y  1, x
1, x  y =
y =  y
y  x
x  ,
,
(x  y)* =
y)* =  y x
y x  y =
y = 
 y.
y.
По принципу двойственности:
f * =  yz
yz  (
( (x
(x  (y
(y  z)
z)  1)) =
1)) =  yz
yz 
 z (x
z (x  (y
(y  z)
z)  1) = z (
1) = z (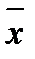 y Ú(
y Ú(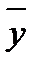 x Å
x Å  z Å
z Å  )) = z (
)) = z (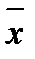 y Ú
y Ú  (x Å z Å1)) = z (
(x Å z Å1)) = z ( y Ú
y Ú  (x Å
(x Å  )) = z
)) = z  y Ú(z
y Ú(z  x Å z
x Å z 
 ) = z (
) = z (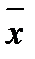 y Ú x
y Ú x  ) = z (x Å y).
) = z (x Å y).
Тогда f = (f *)* = [ z (x Å y)]* = z Ú(x ~ y).
Пример 5. Найти формулу для f* и показать, что она эквивалентна формуле N = (x Ú(z Å t))  , если f = (xyz ~(t Ú x
, если f = (xyz ~(t Ú x  ))Ú
))Ú  t.
t.
f * = ((x Ú y Ú z)Å t ( Ú y))(
Ú y))( Ú t) = (
Ú t) = ( t (
t (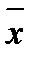 Ú y)Ú(x Ú y Ú z)
Ú y)Ú(x Ú y Ú z)  )(
)( Ú t) =
Ú t) =
= (

 t Ú(x Ú y Ú z)(
t Ú(x Ú y Ú z)( Ú x
Ú x  ))(
))(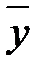 Ú t) =
Ú t) = 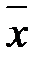

 t Ú(x Ú y Ú z)(
t Ú(x Ú y Ú z)(
 Ú x
Ú x  Ú tx
Ú tx 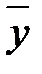 ) =
) =
= 

 t Ú(x Ú y Ú z)(
t Ú(x Ú y Ú z)(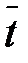
 Ú x
Ú x 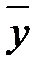 ) =
) =  (
( x Ú
x Ú  t Ú
t Ú  z Ú x Ú xz) =
z Ú x Ú xz) = 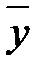 (
( t Ú x Ú
t Ú x Ú  z Ú xz)
z Ú xz)
=  (x Ú(z Å t)).
(x Ú(z Å t)).
|
|
|


