 |
Лемма о несамодвойственной функции
|
|
|
|
Подстановкой функций 
и 
в несамодвойственную функцию можно получить одну из констант.
Доказательство. Пусть 
– несамодвойственная функция. Тогда существует набор 
, для которого 
. Построим функцию 
, заменив единицы в 
на 
, а нули – на 
. Так как 
, то 
. Заметим, что 
.
Тогда 
, т.е. 
. Следовательно, функция 
есть одна из констант.
Теорема о разложении функции по переменным
Пусть f ( x 1,..., xn ) Î P 2. Тогда для любого m: 1 ≤ m ≤ n допустимо представление:
f ( x 1,..., xm, xm +1,..., xn ) = 
,
где дизъюнкция берется по всем наборам из 0 и 1, которое называется разложением функции f по переменным x 1,..., xn.
Прежде чем доказать утверждение, рассмотрим примеры.
Пример 1. m = 1, запишем разложение по переменным х:
f (x 1,..., xn) = 
= 
f (0, x 2 , …, xn)Ú x 1 f (1, x 2,..., xn). (1)
Пример 2. m =2, запишем разложение по переменным х и 
:
f (x 1, x 2,… x n) = 
=
.
Если f (x 1, x 2) = x 1 Å x 2, то последняя формула дает x 1 Å x 2 = 
x 2Ú x 1 
.
Доказательство. Для доказательства возьмем произвольный набор (a 1,..., a n) и покажем, что левая и правая части формулы (1) принимают на этом наборе одинаковые значения. Слева имеем f (a 1,..., an). Cправа: 
.
Дизъюнкция берется по всевозможным наборам (s 1,..., sm). Если в этих наборах хотя бы одно si ¹ ai (1≤ i ≤ m), то 
= 0 и 
, следовательно, ненулевой член будет только на наборе (s 1,..., sm) = (a 1,..., am), тогда 
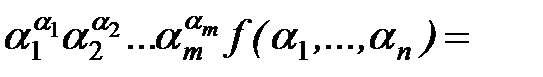f (a 1,..., an).
Следствие 1. Любую функцию f ( x 1,..., xn ) не равную тождественно нулю можно представить в виде: 
, причём единственным образом. Этот вид называется совершенной дизъюнктивной нормальной формой функции f ( x 1,..., xn ) и записывается СДНФ.
Доказательство. Существование СДНФ для функции не равной тождественно нулю вытекает из предыдущей теоремы. Покажем, что эта СДНФ единственная. В самом деле, имеется 
n -местных функций, не равных нулю тождественно. Подсчитаем число различных СДНФ от n переменных. Путь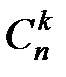 
означает число сочетаний из n элементов по k. Тогда число одночленных СДНФ 
равно 
. Число k -членных СДНФ равно 
. Число n -членных СДНФ равно 
. Число всех различных СДНФ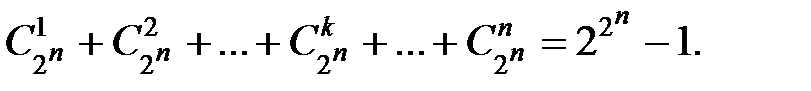 
|
|
|
Итак, 
функций реализуются посредством 
СДНФ, т.е. каждой функции соответствует единственная СДНФ.
Замечание. 
– элементарная конъюнкция ранга n по числу входящих переменных, предполагается, что при i ¹ j, хi ¹ хj. СДНФ для f (x1,..., xn) – дизъюнкция элементарных конъюнкций ранга n. Если функция представлена в виде дизъюнкций элементарных конъюнкций, где ранг хотя бы одной элементарной конъюнкции меньше n, то такая форма называется дизъюнктивной нормальной формой (ДНФ).
Cледствие 2. Любая функция алгебры логики может быть представлена в виде формулы через отрицание, & и Ú.
а) Если f ≡ 0, то f (x 1,..., xn) = 
& 
.
б) Если f (x 1,..., xn) ¹ 0 тождественно, тогда ее можно представить в виде СДНФ, где используются только связки 
, &, Ú. СДНФ дает алгоритм представления функции в виде формулы через &, Ú, 
.
Следствие 3. Мы умеем представлять функцию в виде 
. Нельзя ли представить ее в виде 
. Пусть функция f ( x 1,..., xn ) ¹ 1 тождественно. Тогда функция f * ¹ 0 тождественно, и ее можно представить в виде СДНФ:
.
По принципу двойственности заменим & на Ú и наоборот, получим
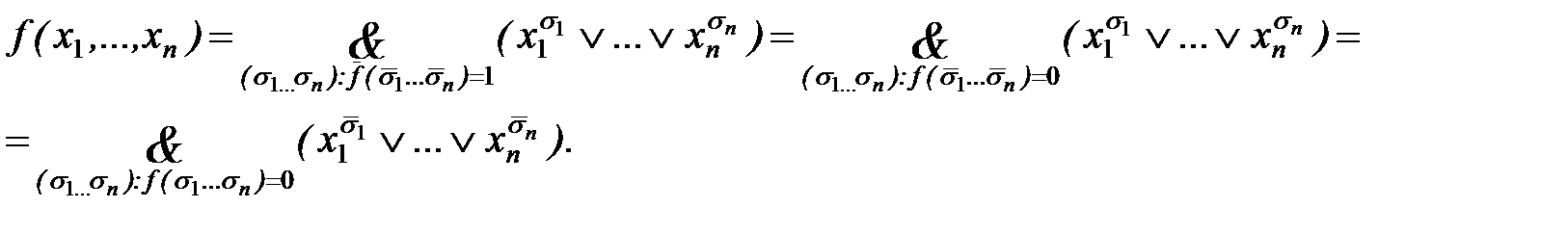(2)
называется элементарной дизъюнкцией ранга n. Представление функции в виде (2) называется совершенной конъюнктивной нормальной формой или в краткой записи – СКНФ. СКНФ для f (x 1,..., xn) – конъюнкция элементарных дизъюнкций ранга n. КНФ для f (x 1,..., xn) – конъюнкция элементарных дизъюнкций, где ранг хотя бы одной элементарной дизъюнкции меньше n.
Пример 4. Пусть f (x 1, x 2, x 3) = x 1 
(x 2 (x 3 ~ x 1)). Представим ее в виде СКНФ, для этого получим таблицу истинности.
| x 1 | x 2 | x 3 | x 3~ x 1 | x 2 (x 3~ x 1)
| f |
| 1 | 1 | 1 | 1 1 | 1 | 1 |
Функция равна нулю только на наборе (1, 1, 0), поэтому
|
|
|
f (x 1 x 2 x 3)= x 1 
Ú x 2 Ú x 3 
= x 10Ú x 20Ú x 31= 
Ú 
Ú x 3.
|
|
|
