Особенности современной зарубежной географии

 

К ним можно отнести следующее.

1. До первой мировой войны ведущие позиции в зарубежной географии занимали немецкие географы. Но в период между двумя мировыми войнами официальная немецкая география дискредитировала себя в глазах объективных исследователей (в стране у власти стояли нацисты; правительство непосредственно вмешивалось в дела науки).

Главное течение географической мысли, которое возобладало в Германии в период между войнами, было связано с попыткой приложения географических понятий к политике. Оно получило название “геополитика” (Geopolitik). По Карлу Хаусхоферу (1924), геополитика - это умение и искусство использовать географические знания для выработки и обоснования политики государства. Хаусхофер основал журнал “Zeitschrift fur Geopolitik”, который стал главным проводником и распространителем сочинений, поддерживающих нацистскую политику. После краха фашистской Германии в 1945 г. К. Хаусхофера судил Нюрнбергский трибунал, а в 1946 г. он кончил жизнь самоубийством.

2. К 1960-м годам немецкая география во многом возвратила себе утраченные позиции. В ФРГ несколько видных географов независимо друг от друга углубленно работали и в области физической, и в области экономической (социальной) географии. Среди них особенно выделились Г. Бобек, Г. Мортенсон, Г. Шмитхеннер, К. Тролль и другие. При этом постепенно нарастала специализация внутри географии. Так, физическая география подразделилась на геоморфологию, геофизику, метеорологию, климатологию, океанологию и другие дисциплины. Культурная (социальная) география также подверглась дроблению. Вместе с тем значительное внимание ландшафтному синтезу уделили географы как в ФРГ (Карл Тролль, Йозеф Шмитхюзен, Карл Паффен), так и в ГДР (Эрнст Нееф, Гюнтер Хаазе, Ганс Рихтер и другие).

3. Американский стереотип географии сформировался под сильным влиянием немецкого географа А. Геттнера, идеи которого в 30-е годы перенес на американскую почву Р. Хартшорн (1939). Традиционная американская география - это пространственная (хорологиче­ская, или региональная) наука. Географа интересуют индивидуальные особенности отдельных мест (территорий, районов), а не общие закономерности. В Америке принято рассматривать географию как единую науку, без подразделения на отдельные отрасли (физическую, экономическую, биогеографию и т.д.). Почти всеобщим признанием среди географов США пользуется взгляд о том, что география - наука социальная.

Развитие американской географии прошло за последние десятилетия сложный путь. В книге П. Джеймса и Дж. Мартина (1988 г.) отмечено несколько научных направлений, типичных для первой половины XX в. В их числе энвайронментализм - учение о “географиче­ском контроле” над судьбами человечества. Это направление, однако, довольно скоро вышло из моды. Как путевая веха в истории американской географической мысли характеризуется труд Р. Хартшорна “The Nature of geography”, вышедший в 1939 г. Авторы констатируют все больший отход географии США от изучения природы в сторону культурных явлений, в сторону регионализма и антропоцентризма.

В последний период географы традиционного направления в США оказались неподготовленными для участия в разработке проектов территориального развития, и особенно для решения острейших социальных и экологических проблем. Многие американские географы, преимущественно из молодого поколения (Вильям Бунге, Дэвид Харвей, Эдвард Тейф, Ричард Морилл и многие другие), увидели альтернативу традиционному направлению в квантификации, т.е. в широком использовании количественных методов в географических исследованиях. Представители этого направления надеялись создать теоретическую географию с помощью математических, а также физических (со­циальная физика) моделей и системного подхода. На практике, однако, речь шла только о явлениях социальной сферы в их чисто размещенческом аспекте и, несмотря на видимость новизны, принципы хорологического взгляда на географию не затрагивались. Р. Джон­стон заметил, что в американской географии в результате “количе­ственной революции” отхода от хартшорновского определения географии не произошло, и “конечная цель географических исследований, как ее сформулировал Хартшорн, осталась прежней” (Джонстон Р. География и географы. М.: Прогресс, 1987. С. 100, 133).

 

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ

 

Джеймс П., Мартин Дж. Все возможные миры. История географических идей. М.: Прогресс, 1988. 672 с.

Исаченко А.Г. География сегодня: Пособие для учителей. М.: Просвещение, 1979. 192 с.

Марков К.К., Суетова И.А., Добродеев О.П., Симонов Ю.Г. Введение в физическую географию: Учебное пособие для географических факультетов университетов. М.: Высшая школа, 1973. 183 с.

Мукитанов Н.К. От Страбона до наших дней. Эволюция географических представлений и идей. М.: Мысль, 1985. 237 с.

Саушкин Ю.Г. Географическая наука в прошлом, настоящем, будущем: Пособие для учителей. М.: Просвещение, 1980. 269 с.

Саушкин Ю.Г. История географических идей // Мир географии. География и географы. Природная среда. М.: Мысль, 1984. С. 60-77.

Энциклопедия для детей. Т. 3. География. 2-е изд., перераб. и доп. / Глав. ред. М.Д. Аксенова. М.: Аванта+, 1997. 704 с.

Глава II. СТРОЕНИЕ СОЛНЕЧНОЙ СИСТЕМЫ

Планеты и законы их обращения

 

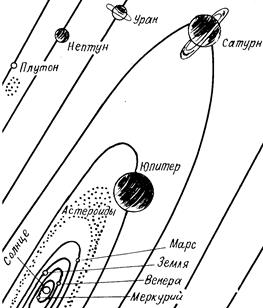Рис. II.1. Солнечная система

Солнечная система включает девять крупных планет, которые со своими 57 спутниками обращаются вокруг массивной звезды по эллиптическим орбитам (рис. II.1). По своим размерам и массе планеты можно разделить на две группы: планеты земной группы, расположенные ближе к Солнцу, - Меркурий, Венера, Земля и Марс и планеты-гиганты - Юпитер, Сатурн, Уран и Нептун, находящиеся на значительно более удаленных от центральной звезды орбитах. Последняя из известных планет - Плутон - своей орбитой с радиусом около 6 млрд. км очерчивает границы Солнечной системы. Плутон не относится к планетам-гигантам, его масса почти в 10 раз меньше массы Земли. Аномальные характеристики этой крошечной планеты позволяют рассматривать ее как бывший спутник Нептуна.

Кроме больших планет между орбитами Марса и Юпитера вращается более 2300 малых планет - астероидов, множество более мелких тел - метеоритов и метеорной пыли, а также несколько десятков тысяч комет, двигающихся по сильно вытянутым орбитам, некоторые из которых далеко выходят за границы Солнечной системы.

Все планеты и астероиды обращаются вокруг Солнца в направлении движения Земли - с запада на восток. Это так называемое прямое движение. Основные закономерности движения планет полностью определяются законами Кеплера. Рассмотрим эти законы и охарактеризуем основные элементы эллиптических орбит.

Рис. II.2. Элементы планетной орбиты: АП - большая полуось орбиты, ось апсид; П - перегилий; А - афелий; r - радиус-вектор

Согласно первому закону, все планеты обращаются вокруг Солнца по эллиптическим орбитам, в одном из фокусов которых находится Солнце. На рис. II.2 показаны элементы планетных орбит с Солнцем (С) в фокусе. Линия АП называется линией апсид, крайние точки которой афелий (А) и перигелий (П) характеризуют наибольшее и наименьшее удаление от Солнца. Расстояние планет (Р) на орбите от Солнца (гелиоцентрическое расстояние) определяется радиусом-вектором r =СР. Отношение полуфокального расстояния (с) к большой полуоси (а) называется эксцентриситетом орбиты:

e = . (II.1)

 

Если обозначить через qперигельное расстояние, а через Q - афелийное расстояние, то их значения легко определить из выражений:

 

q = а - с = а(1 - е), (II.2)

 

Q = а + с = а(1 + е). (II.3)

 

Тогда, определив большую полуось (а), мы найдем среднее годичное расстояние планеты до Солнца:

 

а = . (II.4)

 

Cреднее гелиоцентрическое расстояние Земли от Солнца равно 149,6 млн. км. Эта величина называется астрономической единицей и принимается за единицу измерений расстояний в пределах Солнечной системы.

Согласно второму закону Кеплера, радиус-вектор планеты описывает площади, прямо пропорциональные промежуткам времени. Если обозначить через S₁ площадь перигелийного сектора (рис. II.3), а через S₂ - площадь афелийного сектора, то их отношение будет пропорционально временам t₁ и t₂,за которые планета прошла соответствующие отрезки дуг орбиты:

 

Рис. II.3. Площади, описываемые радиус-вектором планеты

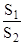= . (II.5)

 

Отсюда следует, что секториальная скорость -

 

V = 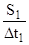= = const - (II.6)

величина постоянная.

Время, в течение которого планета сделает полный оборот по орбите, называется звездным, или сидерическим, периодом Т (рис. II.3). За полный оборот радиус-век­тор планеты опишет площадь эллипса:

 

S= pab=p a² . (II.7)

 

Поэтому секториальная скорость

 

V = = 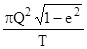(II.8)

 

оказывается наибольшей в перигелии, а наименьшей - в афелии. Используя второй закон, можно вычислить эксцентриситет земной орбиты по наибольшему и наименьшему суточному смещению Солнца по эклиптике, отражающему движение Земли (см. § 2). Земля в перигелии пребывает в начале января (h_max=61'), а в афелии в начале июля (h_max = 57'). По второму закону Кеплера скорость Земли в афелии и перигелии определяется из выражений:

 

V_Q=h_minQ, V_q=h_maxq. (II.9)

 

Учитывая закон сохранения момента количества движения

 

V_q· q = V_Q· Q (II.10)

 

и подставив сюда значения (II.9) с учетом выражений (II.2) и (II.3), найдем:

= 1,03397, откуда е= 0,0167.

 

Таким образом, орбита Земли лишь ненамного отличается от окружности.

Согласно третьему Закону Кеплера, квадраты сидерических периодов обращения планет (Т₁² и Т₂²) прямо пропорциональны кубам их средних расстояний от Солнца (а₁³ и а₂³):

 

. (II.11)

 

Если одна из планет - Земля, период ее сидерического обращения равен Т₁=1 году, а расстояние от Солнца а₁ положить равным а₁=1 а. е., то выражение (II.11) принимает простой вид:

 

Т₂² = а₂³. (II.12)

 

Полученное выражение позволяет по известным из наблюдений периодам обращения планет, других небесных тел вокруг Солнца вычислять их средние гелиоцентрические расстояния.

Найденные эмпирически из наблюдательной астрономии законы Кеплера показали, что Солнечная система представляет собой механическую систему с центром, находящимся в солнечной массе.

Законы Кеплера послужили Ньютону основой для вывода своего знаменитого закона всемирного тяготения, который он сформулировал так: каждые две материальные частицы взаимно притягиваются с силой, пропорциональной их массам и обратно пропорциональной квадрату расстояния между ними.

Математическая формулировка этого закона имеет вид:

 

F = G , (II.13)

 

где M и m - взаимодействующие массы, r - расстояние между ними, G - гравитационная постояная. В системе СИ G= 6,672· 10^-11 м²· кг^-1· с^-2. Физический смысл гравитационной постоянной заключается в следующем: она характеризует силу притяжения двух масс весом в 1 кг каждая на расстоянии в 1 м. Величина Gвпервые была определена в 1798 г. английским физиком Кавендишем с помощью крутильных весов.

Закон Ньютона решил задачу о характере действия силы, управляющей движением планет. Это сила тяготения, создаваемая центральной массой Солнца. Именно эта сила не дает планетам разлететься, а сохраняет их в связной системе последовательных орбит, по которым, как на привязи, сотни миллионов лет кружатся большие и малые планеты.

Решая задачу движения двух тел под действием взаимного притяжения, Ньютон аналитически определил законы движения планет в поле тяготения Солнца. Тем самым эмпирические законы Кеплера получили строгое математическое доказательство. Третий же закон был уточнен путем введения масс планет и Солнца:

 

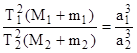. (II.14)

 

Теперь с его помощью оказалось возможным вычислять массы небесных тел. Полагая в выражении (II.14) массы спутников планет m₁ и m₂равными нулю (ввиду их малости в сравнении с массой планет, за исключением Луны) и приняв массу Земли M₂ = 1, получим соотношение (II.14) следующего вида:

= М₁. (II.15)

Воспользуемся законом тяготения и определим массу Земли, полагая, что взаимодействуют две массы - Земли (М) и некоторого тела, лежащего на ее поверхности. Сила притяжения этого тела определяется законом Ньютона:

F = G . (II.16)

 

Но одновременно из второго закона механики эта же сила равна произведению массы на ускорение:

 

F = mg, (II.17)

 

где g- ускорение силы тяжести; R - радиус Земли.

Приравнивая правые части выражений (II.16) и (II.17): G = mg, найдем выражение для определения массы Земли:

М = 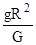. (II.18)

Подставив в (II.18) известные значения G = 6,672 · 10^-11 м² · кг^-1 · с^-2, g = 9,81 м/с², R = 6,371 · 10⁶ м, в итоге получим M₃= 5,97 · 10²⁴ кг, или в граммах: M₃ = 5,97 · 10²⁷ г. Такова масса Земли. Обращаем внимание на формулы (II.16), (II.17), (II.18) - их надо твердо помнить. В дальнейшем мы часто будем пользоваться ими как исходными для определения входящих в них параметров.

Теперь воспользуемся уточненным третьим законом Кеплера и найдем из выражения (II.15) массу Солнца. Для этого рассмотрим две системы тел - Солнце с Землей и Землю с Луной. В первой системе a₁ = 149,6 · 10⁶ км, Т₁ = 365,26 сут; во второй системе а₂ = 384,4·10³ км, Т₂ = 27,32 сут. Подставляя эти значения в формулу (II.15), находим массу Солнца в относительных единицах массы Земли М₀ = 328700 М_3.Полученный результат отличается от более точных расчетов, так как в сравнении с массой Земли массу Луны нельзя приравнивать к нулю (масса Луны составляет ¹/₈₁ массы Земли). Зная массу Земли в абсолютных единицах (килограммах или граммах) и взяв более точное определение массы Солнца (М₀ = 333000 М₃), определим его абсолютную массу: М₀ = 333000·5,97·10²⁷ г = 1,98·10³³ г.

В настоящее время для более точного определения массы и фигуры планет и их спутников используются параметры орбиты искусственных спутников, запускаемых с Земли.

Дальше мы увидим, что закон тяготения Ньютона объясняет не только движение системы планет и других космических объектов в Солнечной системе, но и лежит в основе понимания процессов, происходящих внутри самих астрономических масс.

 

§ 2. Орбитальные характеристики планет

 

Физические условия на поверхности каждой из девяти планет всецело определяются их положением на орбите относительно Солнца. Ближайшие к светилу четыре планеты - Меркурий, Венера, Земля и Марс - имеют сравнительно небольшие массы, заметное сходство в составе слагающего их вещества и получают большое количество солнечного тепла, ощутимо влияющего на температуру поверхности планет. Две из них - Венера и Земля - имеют плотную атмосферу, Меркурий и Марс атмосферы практически не имеют.

Планеты-гиганты Юпитер, Сатурн, Уран и Нептун значительно удалены от Солнца, имеют гигантские массы и плотную мощную атмосферу. Все они отличаются высокой осевой скоростью вращения. Солнечное тепло почти не достигает этих планет. На Юпитере оно составляет 0,018·10³ Вт/м², на Нептуне - 0,008·10³ Вт/м².

Все планеты, за исключением Меркурия и Венеры, имеют спутники, общее число известных на сегодняшний день достигает 57. Наибольшее количество спутников имеют: Юпитер - 16, Сатурн - 17 и Уран - 15. Остальные планеты имеют один-два спутника.

Большая часть массы вещества Солнечной системы сосредоточена в самом Солнце - более 99%. На долю планет приходится менее 1% общей массы. Остальное вещество рассеяно в астероидах, кометах, метеоритах, метеорной и космической пыли.

Все планеты имеют относительно небольшие размеры и в сравнении с расстояниями между ними их можно представлять в виде материальной точки. Из курса физики известно, что произведение массы тела на его скорость называется импульсом:

 

Р = m · V, (II.19)

 

а произведение радиуса-вектора на импульс - моментом импульса:

 

L = r · Р = r · m · V. (II.20)

 

Из приведенного выражения видно, что скорость V движения планеты по эллиптической орбите меняется вместе с изменением радиуса-вектора r. При этом на основании второго закона Кеплера имеет место сохранение моментов импульса:

 

r₁ · m · V₁ = r₂ · m · V₂. (II.21)

 

Из (II.21) видно, что при увеличении r₁ скорость V₁должна уменьшаться и наоборот (масса т планеты неизменна). Если выразить линейную скорость V через угловую w

 

V = w · r, (II.22)

 

то выражение для момента импульса планеты примет вид:

 

L = m · w · r². (II.23)

 

Из последней формулы следует, что при сжатии вращающихся систем, т. е. при уменьшении rи постоянстве т,угловая скорость вращения w неизбежно возрастает.

В табл. II.1 приведены орбитальные параметры планет. Хорошо видно, как по мере возрастания радиуса орбиты гелиоцентрического расстояния) уменьшается период обращения и, следовательно, скорость движения планет.

Таблица II.1

Орбитальные параметры планет Солнечной системы

Планета	Радиус орбиты, 109м	Масса, 1027 г	Плотность, г/см3	Экваториальный радиус, 106 м	Период вращения, земные сут или ч	Наклон экватора к орбите, градусы	Период обращения, земные сут
Меркурий	57,9	0,330	5,43	2,439	58,65 сут	2 ± 3	87,96935
Венера	108,2	4,870	5,25	6,051	243,022 (± 006) сут	177,3	224,7
Земля	149,6	5,976	5,52	6,378	23,9345 ч	23,45	365,26
Марс	227,9	0,642	3,95	3,393	24,6299 ч	23,98	686,98
Юпитер	778,3		6,84	71.398	9,841 ч	3,12
Сатурн	1427,0	568,8	5,85	60,33	10,233 ч	26,73
Уран	2869,6	86,87	5,55	26,20	17,24 ч	97,86
Нептун	4496,6	102,0	5,60	25,23	(18,2 ± 0,4) ч	(29,56)
Плутон	5900,1	(0,013)	(0,9)	(1,5)	6,387 сут	(118,5)

 

При движении планеты вокруг Солнца сила притяжения послед­него уравнивается центростремительной силой, приложенной к планете:

G = . (II.24)

 

Отсюда легко найти среднюю орбитальную скорость движения планеты, которая совпадает с круговой скоростью:

 

V = , (II.25)

 

где r = a - расстояние от Солнца; Т - период обращения планеты вокруг светила.

В качестве примера найдем среднюю орбитальную скорость вращения Земли, положив в формулу (II.25) Т = 365,2564 · 86400 с =
= 31,56· 10⁶ с, а = 149,6 · 10⁶ км, получим V = 29,78 км/с.

Обращаем внимание на наиболее крупные спутники планет. Луна - спутник Земли; Ио, Европа, Ганимед и Каллисто - спутники Юпитера; Титан - спутник Сатурна; Тритон - спутник Нептуна. Это самый крупный спутник в Солнечной системе. Диаметр Тритона 6000 км. Три последние планеты имеют также своеобразные кольца, исследование которых с американской межпланетной станции «Вояджер-2» показало, что они состоят из темного материала, фрагменты которого имеют размеры около метра и более. Не исключено, что это каменные обломки разрушившихся небольших спутников или продукты выбросов мощных вулканических взрывов.

 

Приливные взаимодействия

 

Рассмотрим еще одно интересное явление, возникающее под действием взаимного притяжения планеты и обращающегося вокруг него спутника. На Земле внешнее проявление этого явления - приливы и отливы в океане, в ходе которых уровень воды дважды в сутки поднимается до своих максимальных отметок и опускается до минимальных. Это объясняется притяжением Луны между двумя последовательными одноименными кульминациями ее на меридиане данного места и обусловлено тем, что Земля вращается вокруг своей оси быстрее, чем Луна совершает свой полный оборот вокруг Земли. Поэтому интервал времени между смежными циклами приливных явлений составляет 24 ч 50 мин.

Рис. II.4. Приливное взаимодействие системы Земля-Луна

Поясним это на примере - рис. II.4. Представим Луну в виде материальной точки, расположенной на расстоянии r от центра Земли. Радиус планеты положим равным единице, т.е. R = 1, и рассмотрим, какое притяжение испытывают точ­ки на поверхности Земли (А), на том же меридиане на противоположной стороне (В) и в центре - в точке (О). Пусть эти точки имеют единичную массу. Положив массу Луны m, для каждой точки, в соответствии с законом тяготения, можно написать выражения:

 

g_A = ; g_О = ; g_В = . (II.26)

 

Найдем разность ускорений силы тяжести материальных точек А и О:

 

g_A - g_О = Gm·() = Gm .

 

Поскольку расстояния r и 2r много больше единицы, то ими можно пренебречь. В итоге получим:

 

g_A - g_O = dg = . (II.27)

 

Выражение (II.27) характеризует приливообразующую силу, которая, как видим, обратно пропорциональна кубу расстояний между планетой и ее спутником.

Теперь вновь обратимся к рис. II.4. Под действием силы dg точка А удаляется от точки О в направлении к Луне, образуя своеобразный горб на поверхности планеты - прилив. Но точка О в свою очередь также притягивается Луной на бульшую амплитуду, чем точка В, расположенная на обратной стороне Земли. Поэтому и на обратной стороне на поверхности планеты образуется приливное вздутие. Одновременно с двумя областями прилива в точках квадратур, т.е. районах, отстоящих на 90⁰ по меридиану от точек прилива, будет наблюдаться отлив. В ходе вращения Земли приливные волны дважды в сутки обходят ее поверхность. Высота прилива в океане не превышает 1-2 м. Однако когда приливная волна подходит к шельфовому мелководью, она возрастает до нескольких метров. Волны прилива наблюдаются и в твердой коре и достигают 51 см при сложении поля тяготения Луны и Солнца. Приливное трение, возникающее при движении жидкой и (в меньшей степени) твердой волн, приводит к торможению осевого вращения Земли и ее спутника. По этой причине Луна уже давно прекратила свое вращение вокруг оси и постоянно обращена к планете одной стороной. Уменьшение скорости вращения Земли составляет 2 с за каждые 100 тыс. лет. За последние 450 млн. лет она уменьшилась: вместо 21 ч 53 мин сутки стали составлять 24 ч в настоящее время.

Поскольку масса Земли в 81 раз больше массы Луны, то величина приливного ускорения на поверхности спутника будет примерно в 20 раз больше, чем на Земле, и теоретическая высота твердого прилива может достигать нескольких метров.

В связи с этим возникает интересный вопрос о предельно допустимом расстоянии, на которое могут сблизиться спутник и планета в ходе своей эволюции. Для этого приравняем правую часть выражения (II.27) ускорению свободного падения на поверхности планеты:

 

.

 

После преобразований получим:

 

r» R . (II.28)

 

Здесь m, r и r - масса, радиус и плотность спутника, М, R и r₁ - масса, радиус и плотность планеты. Полученное выражение называется пределом Роша. Спутник, попавший внутрь предела Роша вследствие многокилометровой приливной волны, будет неизбежно разрушен и превращен в каменное кольцо вокруг планеты. Не менее катастрофичными будут последствия такого сближения и для планеты. Гигантский приливный горб высотой многие сотни метров, многократно прокатившись по поверхности планеты по мере приближения спутника, перемелет в пыль горы и равнины, реки и моря планеты, а приливное трение раскалит поверхность разрушившихся пород. Резко затормозится скорость вращения планеты, что вызовет изменение ее фигуры и сопутствующие этому процессу землетрясения. Поверхность планеты претерпит катастрофические разрушения. В свете сказанного гипотеза об образовании Тихого океана путем отрыва Луны представляется просто наивной. При входе в зону Роша она была бы превращена в пыль, сквозь которую мы до сих пор не могли бы видеть солнечного света, не говоря уже о том, что в геологической истории Земли подобной катастрофы не запечатлено. Найдем предел Роша для Земли, положив в формуле (II.29) плотности спутника и планеты примерно одинаковыми. Тогда r» R 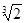» 8400 км, где R = 6371 м - радиус Земли.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: