Дифференцирование оригинала

, (2.6)

 

,

где .

При нулевых начальных условиях

.

Интегрирование оригинала

 

. (2.7)

 

4. Теорема о свертке (умножения в комплексной области)

 

. (2.8)

 

5. Теорема разложения.

Если  где

то оригинал, в соответствии с теоремой Коши о вычетах может быть определен как сумма вычетов по полюсам подынтегральной функции

 

 (2.9)

 

6. Теорема о предельных значениях функции.

 

Начальное значение функции: 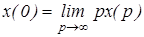. (2.10)

 

Конечное значение функции: . (2.11)

 

7. Теорема запаздывания

 

. (2.12)

Дифференциальные уравнения САУ

 

При математическом описании систем автоматического управления составляют уравнения статики и динамики.

Уравнения статики описывают установившиеся режимы и, как правило, являются алгебраическими.

Уравнения динамики описывают переходные процессы в системах автоматического управления и представляют собой дифференциальные, интегро-дифференциальные или разностные уравнения.

Уравнения динамики системы составляются на основе уравнений отдельных элементов, входящих в систему. Уравнения элементов записываются на основе физических законов, определяющих поведение данного элемента, чаще всего это законы сохранения энергии (Кирхгофа, Ньютона, и др.).

В качестве примера рассмотрим порядок составления уравнения динамики для RLC – четырехполюсника (рис. 4).

 

 

В соответствии сзаконом Кирхгофа можно записать уравнения

 

 

Выполнив преобразования, получим дифференциальное уравнение данной цепи.

 

 

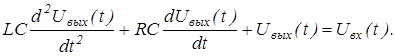
Из условия равенства нулю производных, получим уравнение статики

Линеаризация дифференциальных уравнений

 

Обычно дифференциальные уравнения САУ являются нелинейными вследствие нелинейности характеристик элементов системы (порог чувствительности, ограничение по мощности, трение, люфт, зазор, гистерезис и др.). Решение нелинейных уравнений существенно сложнее, чем линейных. Поэтому всегда, если это возможно, необходимо преобразовать нелинейное уравнение к приближенному линейному, т.е. выполнить линеаризацию.

Линеаризация – замена нелинейного уравнения приближенным линейным. Линеаризация возможна при следующих условиях:

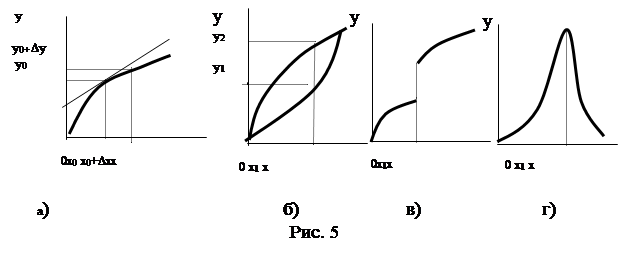
Если отклонения переменных D x и D y относительно установившихся значений x₀ и y₀ малы (рис. 5а). Это условие выполняется для широкого класса систем автоматического управления (например, для замкнутых систем).

2. Система не содержит существенно – нелинейных элементов, т.е. характеристики должны быть однозначными и не иметь разрывов 1-го или 2-го рода (рис. 5б-г).

 

 

Линеаризация осуществляется путем разложения нелинейной функции в ряд Тейлора в окрестности точки, соответствующей установившемуся режиму.

Выразим переменные x и y через их установившиеся значения x₀ и y₀ и отклонения D x и D y.

При этом

               (3.1)

 

Разложение в ряд Тейлора имеет вид:

(3.2)

 

Вычтем уравнение установившегося режима, что соответствует переносу начала координат в точку (x₀, y₀), при этом получим линеаризованное уравнение:

  (3.3)

 

Отличие линеаризованного уравнения от исходного нелинейного:

Линеаризованное уравнение линейное.

2. Линеаризованное уравнение приближенное.

3. Линеаризованное уравнение это уравнение в отклонениях (вариациях).

 

 

Литература

1. Автоматизированное проектирование систем автоматического управления. / Под ред. В.В. Солодовникова. – М.: Машиностроение, 1990. -332 с.

2. Бесекерский В.А., Попов Е.П. Теория систем автоматического регулирования, издание третье, исправленное. Москва, издательство «Наука», Главная редакция физико-математической литературы, 1975.

3. Гринченко А.Г. Теория автоматического управления: Учебн. пособие. – Харьков: ХГПУ, 2000. –272 с.

4. Зайцев Г.Ф. Теория автоматического управления и регулирования. – 2-е изд., перераб. и доп. Киев, Издательство Выща школа Головное издательство, 1989.

5. Справочник по теории автоматического управления. /Под ред. А.А. Красовского – М.: Наука, 1987. – 712 с.

6. Шандров Б.В. Технические средства автоматизации: учебник для студентов высших учебных заведений. Москва, Издательский центр «Академия», 2007.

12	Поделиться:

Воспользуйтесь поиском по сайту: