Уравнение Бернулли для потока реальной жидкости

В реальных потоках жидкости присутствуют силы вязкого трения. В результате слои жидкости трутся друг об друга в процессе движения. На это трение затрачивается часть энергии потока. По этой причине в процессе движения неизбежны потери энергии. Эта энергия, как и при любом трении, преобразуется в тепловую энергию. Из-за этих потерь энергия потока жидкости по длине потока, и в его направлении постоянно уменьшается. Т.е. напор потока H _потока в направлении движения потока становится меньше. Если рассмотреть два соседних сечения 1-1 и 2-2 (рис.3.2) то потери гидродинамического напора Δh составят:

,

где H_1-1 - напор в первом сечении потока жидкости,

H_2-2 - напор во втором сечении потока,

∆h - потерянный напор - энергия, потерянная каждой единицей веса движущейся жидкости на преодоление сопротивлений на пути потока от сечения 1-1 до сечения 2-2.

С учётом потерь энергии уравнение Бернулли для потока реальной жидкости будет выглядеть

Индексами 1 и 2 обозначены характеристики потока в сечениях 1-1 и 2-2.

V

dω

uω

ω

Поток жидкости, как указывалось ранее, можно представить совокупностью элементарных струек жидкости. Скорости по сечению потока неодинаковы, причём в середине потока скорости наибольшие, а к периферии они уменьшаются (струйная модель потока). Это означает, что различные струйки в одном сечении имеют различные значения кинетической энергии. Отсюда следует,

что кинетическая энергия E_п^u, посчитанная с использованием скоростей элементарных струек u_ω, и кинетическая энергия , посчитанная с использованием значения средней скорости потока V, будет иметь разные значения.

Отношение 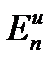и , равное:

,

α носит наименование коэффициент кинетической энергии или коэффициента Кориолиса. Смысл этого коэффициента заключается в отношении действительной кинетической энергии потока в определённом сечении к кинетической энергии в том же сечении потока, но при равномерном распределении скоростей. При равномерном распределении скоростей его значение равно единице, а при неравномерном – всегда больше единицы и для любого потока его значение находится в пределах от 1 до 2 и более. Надо учесть, что в общем случае в разных сечениях потока коэффициент α будет иметь различные значения. В равномерном потоке жидкости, двигающейся по круглым трубам, при ламинарном режиме — α = 2, а при турбулентном можно принимать в среднем α = 1,1.

Если учесть, что характеристики потока V и α зависят от геометрии потока, которая для напорных потоков определяется геометрией трубопровода, понятно, что потери энергии (напора) в разных трубопроводах будут изменяться неодинаково. Показателем изменения напора потока является гидравлический уклонI, который характеризует потери напора на единице длины потока. Физический смысл гидравлического уклона – интенсивность рассеяния энергии по длине потока. Другими словами, величина I показывает, как быстро трубопровод поглощает энергию потока, протекающего в нём

.

Изменение энергии по длине потока удобно проследить на графиках. Из уравнения Бернулли для потока реальной жидкости(закона сохранения энергии) видно, что гидродинамическая линия для потока реальной жидкости (с одним источником энергии) всегда ниспадающая. То же справедливо и для пьезометрической линии, но только в случае равномерного движения, когда скоростной напор а уменьшение напора происходит только за счёт изменения потенциальной энергии потока, главным образом за счёт уменьшения давления P.

 

 

Рис.3.1

Методика проведения эксперимента и обработки

Результатов

Экспериментальная часть

Объектом исследования является участок трубопровода аб (внутренний диаметр трубопровода – 6 мм). К пяти сечениям трубопровода подключены манометры.

Для проведения экспериментов необходимо:

- включить питание стенда;

- включить, нажав кнопку “Пуск”, электродвигатель;

- тумблер Р1 переключить в верхнее положение;

- дать возможность установке поработать в течение 5 – 6 минут;

- для двух значений расхода (настроек регулятора расхода РР) произвести измерения давлений (по манометрам МН1 – МН5). Также необходимо уже описанным выше способом измерить расход и температуру рабочей жидкости.

После проведения экспериментов необходимо отключить питание секундомера, выключить электродвигатель и отключить питание стенда.

Порядок выполнения работы

1. Ознакомиться с лабораторной установкой:

Объектом исследования является участок трубопровода аб (внутренний диаметр трубопровода – 6 мм). К пяти сечениям трубопровода подключены манометры. Внутренний диаметр трубопровода 6 мм.

1.1 измерить и записать в таблицу 1.1 расстояние L каждого сечения от начального а (сечение 1);

1.2 измерить и записать в таблицу 1.1 нивелирную высоту Z для начального и конечного сечений (относительно плоскости сравнения (нулевого уровня), принимаемой за начало отсчета;

1.3 Для проведения экспериментов необходимо:

- включить питание стенда;

- включить, нажав кнопку “Пуск”, электродвигатель;

- тумблер Р1 переключить в верхнее положение;

- дать возможность установке поработать в течение 5 – 6 минут;

- для двух значений расхода (настроек регулятора расхода РР) произвести измерения давлений P (по манометрам МН1 – МН5) и записать в таблицу 1.1 соответствующие их шкале единицы измерения.

Также необходимо уже описанным выше способом (в лабораторной работе 1) измерить расход W, время прохождения заданного объема T и температуру рабочей жидкости t.

После проведения экспериментов необходимо отключить питание секундомера, выключить электродвигатель и отключить питание стенда.

2. Определить и записать в таблицу 2.1

а) площади S используемых в работе поперечных сечений;

б) расходы жидкости Q (секундомер используется для определения времени прохождения t через расходомер РА заданного объема жидкости W (с тем, чтобы в дальнейшем определять расход жидкости в трубопроводе).

в) средние по сечению скорости v потока из уравнения неразрывности Q = υ S;

Среднерасходная скорость υ течения по трубе определится в виде:

;

где Q – расход масла, [м³/с]; d = 0,06 м – диаметр трубопровода.

г) скоростные напоры H_υ = α υ² / 2 g, коэффициент кинетической энергии α взять с учетом режима движения жидкости;

д) пьезометрический напор р/ ρg из формулы Н _п = z+ р/ ρg;

 

е) полные напоры:

;

3. Определить и записать в таблицу 3.1:

а) потери напора h, т. е. разность полных напоров Δ Н для участков 1–2 и 2–3,3-4 и 4-5 по уравнению Бернулли

 

б) гидравлические уклоны для участков для участков 1–2 и 2–3,3-4 и 4-5, используя формулу для ламинарного течения жидкости в трубах круглого сечения:

в) потери давления на этих участках D Р.

 

г) перепад давления на участке трубопровода а - б соответствует потерям давления на этом участке. Он связан с показаниями манометра

D p = ρgD Р,

 

где ρ =894 кг/м³ – плотность масла, применяемого в качестве рабочей жидкости в системе.

 

4. Построить на бумаге, имеющей координатную сетку, в масштабе гидродинамическую (напорную) Н = f ₁(L), пьезометрическую Н _п = f ₂(L) и нивелирную z = f ₃(L) линии (рис 3.4).

 

5. На графике для двух сечений (где потери напора наибольшие), показать все составляющие уравнения Бернулли, т. е. z, p/ ρg, Н _п, Н _υ, H и h.

Таблица 1.1

Сечения	L	Z	P	W	T

 

Таблица 2.1

Сечения	S	Q	υ	p/ρg	H υ	Н п	H

 

Таблица 3.1

Номера участков	h	i	D Р	D p
1-2
2-3
3-4
4-5

 

Содержание отчета

 

1. Титульный лист.

2. Цель работы.

3. Схема экспериментальной установки.

4. Основные рабочие формулы.

5. Таблицы с результатами измерений и расчетов.

6. График

7. Выводы по работе.

⇐ Предыдущая12

Поделиться:

Воспользуйтесь поиском по сайту: