 |
Основные характеристики средств измерений
|
|
|
|
Вадим Юрьевич Кончаловский
Лекции по курсу
МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ И СЕРТИФИКАЦИЯ
Содержание стр.
1. МЕТРОЛОГИЯ………………………………………………………….. 3
1.1. Определение метрологии……………………………………………... 3
1.2. Виды средств измерений……………………………………………… 12
1.3. Основные характеристики средств измерений……………………… 14
1.3.1. Диапазон измерения………………………………………………… 14
1.3.2. Цена деления шкалы и значение единицы младшего разряда…… 14
1.3.3. Точность……………………………………………………………... 16
1.3.4. Характеристики, отражающие влияние прибора на объект……… 23
1.4. Виды и методы измерений……………………………………………. 28
1.5. Представление результатов измерений………………………………. 31
1.5.1. Составляющие погрешности измерения………………………….... 31
1.5.2. Запись результата измерения……………………………………….. 32
1.5.3. Вычисление погрешностей измерения……………………………… 33
2. СТАНДАРТИЗАЦИЯ……………………………………………………. 37
2.1. Определение……………………………………………………………. 37
2.2. Цели стандартизации…………………………………………………... 37
2.3. Принципы стандартизации……………………………………………. 37
2.4. Методы стандартизации………………………………………………. 38
2.5. Виды стандартов……………………………………………………….. 39
2.6. Национальные органы по стандартизации…………………………… 40
2.7. Международное сотрудничество в сфере стандартизации……………. 41
3. СЕРТИФИКАЦИЯ……………………………………………………….. 43
3.1. Определение сертификации…………………………………………. 43
3.2. История сертификации………………………………………………. 43
3.3.Подтверждение соответствия………………………………………… 44
|
|
|
3.3.1. Цели подтверждения соответствия………………………………… 44
3.3.2. Принципы подтверждения соответствия………………………….. 45
3.3.3. Формы подтверждения соответствия……………………………… 45
Литературные ссылки…………………………………………………….... 53
МЕТРОЛОГИЯ
Определение метрологии
МЕТРОЛОГИЯ
наука о… (геология, биология и т.п.)
метро? метр – мера длины, но метрология гораздо старше метра: метр «родился» в 1790 г. во Франции.
Слово «метр»происходит от греческого μετρον – МЕРА.
Старинное понимание: метрология – наука о мерах. Современное понимание шире: метрология – это наука об измерениях.
Итак:
· измерения
· их единство
· их точность
ИЗМЕРЕНИЯ
Объекты материального мира имеют бесчисленное множество различных свойств: объём, масса, цвет и т.д. Для многих свойств применимы понятия «больше» – «меньше», например, масса Земли больше массы Луны; вкус лимона более кислый, чем апельсина. Для некоторых свойств применимы не только понятия «больше» – «меньше», но и во сколько раз больше или меньше: масса Земли в 81 раз больше массы Луны (приблизительно). Но нельзя сказать, что лимон во сколько-нибудь раз, например, в два раза кислее апельсина. А почему нельзя? Потому что для массы существует единица измерения – килограмм – а для вкусовых ощущений она ещё не создана.
Те свойства, для которых существуют единицы измерения, называют
ФИЗИЧЕСКИМИ ВЕЛИЧИНАМИ:
длина, масса, сила электрического тока и т.д.
Физические величины содержат в себе качественный и количественный признаки. Качественный – что это за величина, например, сила электрического тока. Количественный – сколько единиц содержится в данной физической величине, например, 5,4 А. Здесь 5,4 А – значение силы электрического тока (далее для краткости просто «тока»). Нельзя говорить «величина тока 5,4 А», потому что величина – это сам ток. Надо говорить: «значение тока 5,4 А».
|
|
|
Но вот беда: в разные времена у разных народов для одних и тех же величин были созданы разные единицы. Например, L = 7,05 фут = 2,15 м.
Обилие единиц для одной и той же величины – большое неудобство. В 18 веке в Европе были сотни различных «футов». Постепенно пришли к ограниченному числу систем единиц, а идеал –одна система для всего мира.
В 1960 году большинство стран мира приняло международную систему – в русской транскрипции СИ (система интернациональная), в международной – SI (System International)[1].
Как любая система единиц, она содержит несколько независимых основных единиц:
– единица длины – метр (м);
– единица массы – килограмм (кг);
– единица времени – секунда (с);
– единица силы электрического тока – ампер (А);
– единица термодинамической температуры – кельвин (К);
– единица силы света – кандела (кд);
– единица количества вещества – моль
и множество (больше ста) производных единиц. Они образуются из основных на основе фундаментальных физических законов. Например, вольт:
Физические величины принимают свои значения в широких диапазонах. Чтобы избежать чисел с большим количеством нулей, применяют кратные и дольные единицы:
| 10–12 | 10–9 | 10–6 | 10–3 | 103 | 106 | 109 | 1012 | |
| пико | нано | микро | мили | кило | мега | гига | тера | |
| п | н | мк | м | к | М | Г | Т | |
| p | n | μ | m | k | M | G | T |
В последней строке – международное обозначение, в предпоследней – русское.
Измерить какую-либо физическую величину – это узнать, сколько в ней содержится единиц.
Результат измерения – это именованное число, например,
5,83 мкА
Но как получить это число? Нужно сравнить данную величину с её единицей (или с её дольной единицей). Единица электрического тока – ампер. Но что такое ампер? Как определена эта единица? Вот теоретическое определение:
«Ампер равен силе не изменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенными в вакууме на расстоянии 1 м один от другого, вызвал бы на каждом участке проводника длиной 1 м силу взаимодействия, равную 2×10–7 Н».
|
|
|
Совершенно ясно, что практически всё это недостижимо: бесконечная длина, вакуум. Практически ампер воплощается в эталоне ампера.
До 1992 г. эталон ампера представлял собой т.н. «токовые весы». Это равноплечие рычажные весы, к одному из плеч подвешен соленоид, находящийся внутри другого, неподвижного соленоида, а к другому плечу – гири. Соленоиды соединены последовательно. При отсутствии тока гиря массой m0 уравновешивает подвижный соленоид. При пропускании тока I по соленоидам возникает втягивающая сила kI2, где k зависит от числа витков и геометрических размеров соленоидов. Она уравновешивается гирей с массой m:
,
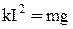откуда
.
Главное требование к эталону – стабильность. Токовые весы дают нестабильность тока I = 1 А практически не превышающую ± 10 мкА.
В 1992 г. введён новый эталон ампера, основанный на открытии квантовых эффектов Джозефсона и Холла [2]. Это позволило снизить нестабильность почти на два порядка: ± 0,15 мкА.
По своему смыслу эталон – это мера. Его назначение – хранить и воспроизводить физическую величину заданного размера.
Но простейшая линейка – это тоже мера, мера длины. Эталоны – это меры высшей точности. Это очень дорогие устройства, которые хранятся в метрологических институтах. Они находятся в специальных помещениях со стабильной температурой. Есть специальная должность – хранитель эталона.
По длинной цепочке размер единицы передаётся от самого точного первичного эталона ко вторичному, далее к рабочим эталонам и наконец доходит до рабочих измерительных приборов и мер.
В некоторых редких случаях для выполнения измерения достаточно только меры: измерение длины линейкой. Длина непосредственно воспринимается зрением. В большинстве же случаев одной меры недостаточно. Например, массу какого-либо тела можно измерить путём взвешивания на рычажных весах. Здесь тоже присутствует мера – это гири, но одних гирь недостаточно, нужны весы. Весы вместе с гирями – это измерительный прибор, в котором мера присутствует непосредственно. Есть другие весы, пружинные, со шкалой и стрелкой.
|
|
|
Теперь можно дать определение понятию «измерение»:
ИЗМЕРЕНИЕ – ЭТО СОВОКУПНОСТЬ ОПЕРАЦИЙ ПО ПРИМЕНЕНИЮ ТЕХНИЧЕСКОГО СРЕДСТВА, ХРАНЯЩЕГО ЕДИНИЦУ ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ, ОБЕСПЕЧИВАЮЩИХ НАХОЖДЕНИЕ СООТНОШЕНИЯ ИЗМЕРЯЕМОЙ ВЕЛИЧИНЫ С ЕЁ ЕДИНИЦЕЙ И ПОЛУЧЕНИЕ ЗНАЧЕНИЯ ЭТОЙ ВЕЛИЧИНЫ.
Это определение содержится в [3]. До этого было принято другое [4], вошедшее во многие книги: «Измерение – это нахождение значения физической величины опытным путём с помощью специальных технических средств».
От термина «измерение» происходит «измерять», но не следует употреблять «мерить», «замерять», «замер» и т.п.
Измерение – широкое понятие. Далее мы будем заниматься электрическими измерениями. Что это значит?
Физические величины могут быть:
· механические – сила, давление, …
· пространства и времени – длина, время, скорость,…
· тепловые – температура, теплоёмкость, теплопроводность, …
· электрические – ток, напряжение, мощность, сопротивление, …
· световые – сила света, световой поток, освещённость, …
· акустические – скорость звука, звуковое давление, …
……
……
Электрические величины в свою очередь можно разделить на:
· активные – ток, напряжение, э.д.с., мощность и др.;
· пассивные (параметрические) – сопротивление, ёмкость, индуктивность, взаимная индуктивность и др.
Кроме того, есть некоторые величины, неразрывно связанные с электрическими – частота, период, фазовый сдвиг.
Под электрическими измерениями понимают:
1) Измерения электрических величин;
2) Измерения временных величин, связанных с электрическими (обычно активными);
3) Измерение неэлектрических величин, преобразованных в электрические, например, измерение температуры с помощью термопары.
Термопара – пример измерительного преобразователя. Его нельзя отнести ни к мерам, ни к измерительным приборам.
Меры, измерительные приборы, измерительные преобразователи – простейшие средства измерений.
ЕДИНСТВО ИЗМЕРЕНИЙ
Понятию «измерение» сопутствует понятие единство измерений. Это очень важное понятие. Существует Закон РФ об обеспечении единства измерений [5]. Что это значит – «единство измерений»? В Законе дано определение:
ЕДИНСТВО ИЗМЕРЕНИЙ – ЭТО СОСТОЯНИЕ ИЗМЕРЕНИЙ, ПРИ КОТОРОМ ИХ РЕЗУЛЬТАТЫ ВЫРАЖЕНЫ В УЗАКОНЕННЫХ ЕДИНИЦАХ И ПОГРЕШНОСТИ ИЗМЕРЕНИЙ НЕ ВЫХОДЯТ ЗА УСТАНОВЛЕННЫЕ ГРАНИЦЫ С ЗАДАННОЙ ВЕРОЯТНОСТЬЮ.
«Узаконенные единицы» – это единицы СИ и некоторые внесистемные единицы, разрешённые к применению (их около 20, например, тонна, гектар).
|
|
|
ТОЧНОСТЬ ИЗМЕРЕНИЙ
Количественно точность измерений характеризуется погрешностями измерений. Есть две формы выражения погрешностей измерение:
· абсолютная погрешность измерения Δ;
· относительная погрешность измерения δ.
Абсолютная погрешность измерения:
, (1)
где Х – результат измерения;
Хист – истинное значение измеряемой величины.
Здесь Хист принципиально неизвестно (иначе, зачем было бы измерять?!), поэтому формула (1) годится только для теоретических исследований. На практике вместо неё применяется другая:
, (2)
где Хд – действительное значение измеряемой величины, достаточно близкое к Хист, так что может использоваться вместо него.
В отличие от Хист значение Хд доступно для практического получения с помощью средства измерений, в достаточной мере более точного, чем данное, давшее результат Х.
Для того, чтобы не путаться в знаке погрешности, запомним, что всегда
ПОГРЕШНОСТЬ – ЭТО ИЗМЕРЕННОЕ МИНУС ДЕЙСТВИТЕЛЬНОЕ
Относительная погрешность измерения:
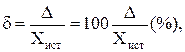
или
Поскольку Δ << Хд, т.е. Х и Хд близки, часто используют формулу
(3)
потому что обычно известно не Хд, а Х.
Выполнив измерение, недостаточно указать только его результат Х. Обязательно нужно определить и указать граничное значение погрешности Δгр при некоторой близкой к единице вероятности, например, при вероятности Р = 0,95. Что это значит? Дело в том, что мы не знаем конкретного значения Δ, но с вероятностью Р можем утверждать, что
– Δгр ≤ Δ ≤ Δгр. (4)
Другими словами, мы не знаем Хист, но с вероятностью Р можем утверждать, что Хист находится в интервале
Х – Δгр ≤ Хист ≤ Х + Δгр. (5)
Бывают случаи, когда без указания Δгр результат Х становится бессмысленным или даже вредным.
Примером может служить древняя задача, которую, по преданию, решал Архимед [6, стр. 14]. Его попросили определить, изготовлена ли корона из золота или это подделка – гораздо более дешёвый сплав, внешне похожий на золото. Архимед знал плотности золота и подозреваемого сплава: ρз = 15,5 г / см3; ρс = 13,8 г / см3. Плотность короны обозначим ρк. Для определения ρк обратились к двум экспертам А и Б. Результаты их работы:
| Эксперт А | Эксперт Б | |
| Оценка ρк, г / см3 | 13,9 | |
| Вероятный интервал ρк, г / см3 | 13,5 – 16,5 | 13,7 – 14,1 |
Покажем эти результаты на графике:
Замечания:
1) Интервалы А и Б перекрываются, значит, оба измерения правильны, т.е. не противоречивы. Если бы интервалы не перекрывались, естественно было бы считать, что хотя бы один эксперт ошибся.
2) Погрешность измерения эксперта А столь велика, что его результат бесполезен: в его интервал попали и ρз и ρс, значит, нельзя узнать, из чего сделана корона.
3) Данные эксперта Б ясно говорят, что корона фальшивая: в его интервал попадает ρс и не попадает ρз.
4) Значит, для того, чтобы по результатам измерений можно было сделать правильный вывод, погрешность измерения не должна быть слишком большой, как у эксперта А. Однако, нет необходимости в том, чтобы она была очень мала. Она должна быть разумно мала, как у эксперта Б.
Главный вывод: оба измерения были бы бессмысленны, если бы они не содержали сведений о погрешностях. Более того, результат эксперта А наталкивал бы на мысль, что корона золотая.
Итак, кроме самого результата измерения должны быть указаны границы интервала, в котором с данной вероятностью находится истинное значение измеряемой величины. Этот интервал называют доверительным интервалом, а эту вероятность – доверительной вероятностью.
Пример записи результата измерения:
(5,481 ± 0,025) мА; Р = 0,95.
Размер доверительного интервала при данной доверительной вероятности характеризует точность. Чем ýже интервал при той же вероятности, т.е. чем меньше погрешность, тем выше точность.
Если интервал не указан, количество разрядов числа, выражающего результат измерения, ориентировочно свидетельствует о точности. Сравните, например, две записи: 5,4 А и 5,43135 А.
При этом не следует думать, что чем точнее, тем лучше. И это не только потому, что чем точнее, тем дороже обойдётся полученный результат. При увеличении точности мы обязательно столкнёмся с тем, что наша мысленная модель объекта перестаёт быть адекватной самому объекту.
Простой пример. Пусть нам надо измерить высоту проёма двери. Мы можем взять рулетку и измерить с погрешностью, не выходящей за пределы ± 0,5 см. Но если мы захотим произвести более точное измерение, например, такое, что погрешность не выходит за пределы ± 0,5 мм, мы обнаружим, что наша модель проёма в виде прямоугольника перестаёт быть адекватной: высота не одинакова по ширине.
Поэтому, строго говоря, понятие физическая величина относится не к самому объекту, а к его модели. По мере уточнения результатов измерений можно переопределять модель. Например, может выясниться, что модель проёма – это не прямоугольник, а трапеция.
Заключение по разделу 1.1.
Мы ввели и определили ряд понятий, связанных с метрологией. Они находятся в определённой взаимосвязи:
Виды средств измерений
|
 |
Меры воспроизводят физическую величину заданного значения. Они бывают однозначные (например, резистор с сопротивлением 10 Ом) и многозначные (линейка, магазин сопротивлений, магазин емкостей).
Измерительные преобразователи преобразуют сигналы измерительной информации в форму, более удобную для дальнейшего использования.
Примеры:
1) Термопара преобразует температуру в термо-э.д.с.;
2) Измерительный усилитель преобразует меньшее напряжение в большее;
3) Измерительный трансформатор тока преобразует больший переменный ток в меньший.
Измерительные приборы преобразуют сигналы измерительной информации в форму, доступную для восприятия человеком.
Остановимся подробнее на измерительных приборах.
Виды измерительных приборов.
а) По измеряемой величине:
– измерители напряжения U – вольтметры V;
милливольтметры mV;
микровольтметры μV;
киловольтметры kV;
– измерители тока I – амперметры А;
• • •
• • •
•
•
•
б) По форме представления результата:
– аналоговые (шкала и указатель);
– цифровые.
в) По выполняемым функциям:
– показывающие;
– регистрирующие;
– показывающие и регистрирующие.
г) По элементной базе:
· электромеханические; вот символы измерительных механизмов:
· электронные:
д) По условиям применения:
Меры, измерительные преобразователи и измерительные приборы – это элементарные средства измерения. С добавлением средств вычислений образуются более сложные: измерительно-вычислительные системы и комплексы.
Основные характеристики средств измерений
Измерительные приборы
1.3.1. Диапазон измерения
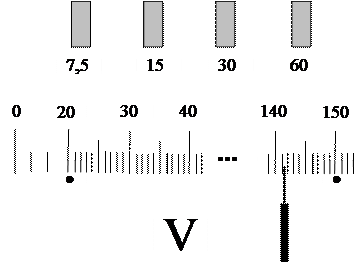Вольтметр с четырьмя поддиапазонами измерения.
Верхние пределы:
7,5; 15; 30 и 60 В
Нижние пределы:
1; 2; 4 и 8 В
Пределы ограничены жирными точками.
Поддиапазоны показаний:
0 – 7,75; 0 – 15,5;
0 – 31 и 0 – 62 В.
Характеристики гарантируются в пределах диапазона измерений.
У приборов с равномерной шкалой диапазоны измерений и показаний совпадают.
Существуют приборы с двусторонними шкалами, например:
– 5 мА ÷ 0 ÷ 5 мА, с безнулевыми шкалами, например: 49 ÷ 50 ÷ 51 Гц.
Верхний предел диапазона показаний может быть бесконечность:
Обратная, существенно неравномерная шкала.
1.3.2. Цена деления шкалы и значение единицы младшего разряда.
Цена деления шкалы – это у аналоговых приборов.
В нашем вольтметре на 1м поддиапазоне с1 = 7,5 / 150 = 0,05 В / дел, а на последнем с4 = 60 / 150 = 0,4 В / дел.
Зачем это нужно? Можно сделать отсчёт в делениях и для получения результата умножить на цену деления: U(В) = α (дел) × с (В/дел). Конечно, в таких простых случаях всё это можно проделывать в уме. Но вот ещё пример – ваттметр (обозначение на циферблате – W). У ваттметра две пары зажимов: для тока и для напряжения. В каждой паре один зажим помечен звёздочкой, а около другого указано номинальное значение тока и напряжения соответственно. При этих значениях стрелка отклониться «на всю шкалу».
Мы видим, что показание прибора в делениях α = 61 дел. Но сколько это ватт? В данном случае обязательно нужно определить цену деления. Шкала содержит 75 делений. Мощность, соответствующая отклонению стрелки «на всю шкалу» – это произведение номинальных значений тока I = 5 А и напряжения U = 150 В. Следовательно, цена деления с = (5×150)/75 = 10 Вт /дел и показание в ваттах Р = 61×10 = 610 Вт.
Кстати: а как правильно подключить ваттметр? Непременное правило: «звёздочка к звёздочке». Если его нарушить, стрелка будет пытаться отклониться влево от нуля. Следовательно, включаем так:
|
 | |||
| |||
Как же лучше?
Почва для размышления!
Значение единицы младшего разряда у цифровых измерительных приборов:
В лучших моделях цифровых вольтметров на первом (самом чувствительном) поддиапазоне значение единицы младшего разряда может быть 10 нВ.
1.3.3. Точность
Количественная характеристика точности – погрешность. Чем меньше погрешность, тем выше точность.
Прежде всего, существуют два понятия:
· погрешность измерения;
· погрешность измерительного прибора.
Это не одно и то же. Можно взять дорогой, очень точный прибор, но получить при неграмотном использовании очень плохой результат. Попробуйте сами привести пример такой ситуации.
Существует три формы выражения погрешностей:
· абсолютная Δ;
· относительная δ:
· приведённая γ.
Погрешность измерения может быть выражена в форме Δ или δ, а погрешность измерительного прибора – в любой из трёх форм.
Абсолютная погрешность измерительного прибора:
Δ = Х – Хист ≈ Х – Хд, (6)
где Х – показание прибора; Хист – истинное значение измеряемой величины;
Хд – её действительное значение.
Относительная погрешность измерительного прибора:
δ = 
δ (%) = 100 
(7)
Приведённая погрешность измерительного прибора:
γ = 
γ (%) = 100· 
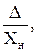(8)
где Хн – нормирующее значение измеряемой величины.
Что значит «нормирующее значение? Покажу на примерах:
1) У вольтметра с диапазоном измерения от 0 до 15 В нормирующее значение
Хн = Uн = 15 В.
2) У миллиамперметра с двусторонней шкалой – 5 мА ÷ 0 ÷ 5 мА нормирующее значение
Хн = Iн = 5 мА (или 10 мА).
3) Частотомер с узким диапазоном измерения 49 Гц ÷ 50 Гц ÷ 51 Гц нормирующее значение
Хн = fн = 50 Гц.
Связь относительной погрешности с приведённой:
δ = γ·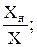 
δ = γ при Х = Хн ; δ > γ при Х < Хн!
Основная погрешность и дополнительные погрешности.
Погрешность Δ зависит от влияющих величин ξ:
Δ = f(ξ1; ξ2;… ξn).
Влияющие величины – это:
а) внешние факторы – температура, напряжение питания (если оно есть у прибора) и др.;
б) неинформативные параметры входного сигнала.
Пример: u(t) = Umsinωt =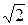 
Usin2πft
– вольтметром измеряют среднее квадратическое значение U синусоидального напряжения u(t); в этом случае частота f этого напряжения – неинформативный параметр входного сигнала, т.е. такой параметр, который не несёт полезной информации о значении U, но влияет на результат измерения U;
– частотомером измеряют частоту f синусоидального напряжения u(t); в этом случае U – неинформативный параметр входного сигнала.
Нормальные условия применения прибора – это такие условия, когда все влияющие величины ξi либо имеют нормальные значения [7]
ξi = ξi,норм,
либо находятся в пределах нормальных областей значений
ξi,норм,min ≤ ξi ≤ ξi,норм,max.
Примеры:
а) θ = 20 0С – нормальное значение температуры, принятое в нашей стране;
б) относительная влажность воздуха от 30 до 80 % – нормальная область значений.
Примечание. Обеспечить при испытаниях точно 20 0С невозможно, поэтому допускаются отклонения, например, в пределах (20 ± 2) 0С. Этот допуск зависит от точности испытуемого прибора; для самых точных он составляет ± 0,5 0С.
ОСНОВНАЯ погрешность Δо – это погрешность в нормальных условиях.
Рабочие условия применения прибора – это такие условия, когда влияющие величины ξi находятся в пределах рабочих областей значений
ξi,раб,min ≤ ξi ≤ ξi,раб,max.
Пример:
температура в пределах 10 0С ≤ θ ≤ 35 0С (2я группа средств измерений)
·
·
·
– 50 0С ≤ θ ≤60 0С (6я группа).
ДОПОЛНИТЕЛЬНАЯ погрешность Δд – это изменение погрешности, вызванное отклонением одной из влияющих величин ξi от её нормального значения ξi,норм или выходом за пределы нормальной области значений ξi,норм,min ÷ ξi,норм,max.
Систематическая и случайная погрешности.
СистематическаяпогрешностьΔсостаётся постоянной или закономерно изменяется в зависимости от времени (или другого аргумента).
Случайная погрешность 
изменяется случайным образом.
Пусть Х = const. Производятся повторные измерения Х. Если Х1; Х2;…Хn отличаются друг от друга – значит, проявляет себя случайная погрешность. Что при этом принять за результат измерения? Ответ известен: среднее значение:
. (9)
В вероятностном смысле Хср ближе к истинному значению Хист, чем любое Хi. Это объясняется тем, что одни Хi отличаются от Хср в одну сторону, другие – в другую. Чем больше n, тем меньше влияние случайной погрешности, но тем дольше процесс измерения.
Такое измерение с повторами и усреднением называют измерением с многократными наблюдениями: Хi – это наблюдения, а Хср – результат измерения.
Таким образом, простой приём – многократные наблюдения – позволяет обнаружить присутствие случайной погрешности, а их усреднение – снизить её влияние.
Заметим, что этот приём не обнаруживает систематическую погрешность и не снижает её.
Для нахождения Δс нужен более точный прибор, показание которого можно считать действительным значением Хд, и тогда
Δс = Х – Хд (10)
или
Δс = Хср – Хд, (11)
если выявлено присутствие случайной погрешности и произведены многократные наблюдения.
Если Δс найдена, её можно исключить, введя поправку:
η = – Δс. (12)
Тогда Х + η – это будет исправленный результат измерения.
Получается, что если погрешность найдена – это уже не погрешность. Погрешность остаётся погрешностью лишь до тех пор, пока в ней есть неопределённость, случайность. После внесения поправки остаются не исключённые остатки Δс, но они уже случайны.
Итак, погрешность – в принципе случайная величина.
Случайные величины можно изучать, у них есть определённые законы. Этим занимается одна из отраслей математики – теория вероятностей. Мы будем её использовать.
Мы рассмотрели случай, когда с помощью более точного прибора находят Δс и вводят поправку η. Может возникнуть вопрос: если у нас есть этот более точный прибор, почему бы им и не измерять? Дело в том, что поправка вносится в результаты многих измерений, а определяется редко. Для её нахождения используются эталонные средства измерения. Они служат не для измерений, а для поверки и аттестации рабочих средств измерения. Если бы эталонные средства использовались для измерений, они быстро бы перестали быть эталонными.
Но вообще внесение поправки – довольно редкий случай в практике измерений: это точные лабораторные измерения, научные исследования. Большей частью Δс есть, но её не выявляют для каждого данного экземпляра средств измерений. На множестве экземпляров данного типа средств измерений она проявляет себя, как случайная величина.
Таким образом, проявляет себя, как случайная величина на множестве многократных наблюдений, если таковые производятся, а Δс проявляет себя, как случайная величина даже при одном измерении – на множестве экземпляров приборов данного типа.
Нормирование погрешностей
Нормируют предельно допускаемые значения погрешностей средств измерений, в первую очередь для основной погрешности. Существуют разные формы нормирования:
1) Нормируют предельно допускаемые значения основной приведённой погрешности, например, γо,п = ± 0,5 %. Так нормируют погрешности аналоговых вольтметров, амперметров и т.п. Это означает, что – 0,5 % ≤ γо ≤ 0,5 %.
Возможно, нам попался экземпляр прибора, у которого γо = 0, но мы этого не знаем. Мы знаем, что гарантируется – 0,5 % ≤ γо ≤ 0,5 %.
2) Гораздо реже гарантируется предельно допускаемые значения основной относительной погрешности, например, δо,п = ± 0,02 %. Так, например, нормируют погрешность измерительных мостов.
3) Нормируют предельно допускаемые значения основной относительной погрешности, но не в виде числа со знаками ±, а в виде формулы:
. (13)
Так нормируют погрешность для цифровых измерительных приборов, например:
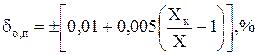
Дополнительные погрешности.
Рассмотрим на примерах.
Пример 1.
В документации читаем: «Дополнительная температурная погрешность не более половины основной на каждые 10 0С в рабочем диапазоне». Расшифруем эту фразу. Пусть известно, что для данного прибора:
– рабочий диапазон температур 5 0С ≤ θ ≤ 40 0С;
– предельные значения основной приведённой погрешности γо,п = ± 0,5 %.
Это значит, что при 10 и при 30 0С к γо добавляется ещё ± 0,25 %. Есть основания считать, что зависимость дополнительной температурной погрешности от температуры близка к линейной. Поэтому, если, например, θ = 35 0С, то предельные значения дополнительной температурной приведённой погрешности будут
.
Здесь 
– температурный коэффициент дополнительной температурной погрешности.
Если бы вместо «…не более половины основной…» было «…не более основной…», то температурный коэффициент был бы 0,1γо,п.
Пример 2.
В документации читаем: «Дополнительная частотная погрешность не более основной». Пусть это относится к аналоговому вольтметру переменного напряжения, у которого нормальная область значений частоты 45 Гц ≤ fнорм ≤ 1 МГц, а рабочая область 20 Гц ≤ fраб ≤ 5 МГц. На циферблате прибора это обозначается так:
20 Гц…45 Гц…1 МГц…5 МГц
 |
Пусть для этого вольтметра γо,п = ± 4 %. Это значит, что в диапазонах от 20 Гц до 45 Гц и от 1МГц до 5 МГц к γо добавляется дополнительная частотная погрешность с предельными значениями γд,f,п = ± 4 %. В случае частотной погрешности нет оснований считать, что она линейно зависит от частоты. Поэтому, если, например, f = 2 МГц всё равно приходится считать, что при этом γд,f,п = ± 4 %.
Это, конечно, плохо, поэтому стандарт [8] предлагает нормировать не дополнительные погрешности, а функции влияния (для линейных функций – коэффициенты влияния).
Классы точности
Класс точности – комплексная характеристика, которая говорит нам и об основной и о дополнительных погрешностях [9].
Обозначение классов точности:
· На циферблате аналогового прибора проставлено число, например, 0,5. Что оно означает? В первую очередь, что γо,п = ± 0,5 %.
· На лицевой панели прибора проставлено число внутри окружности, например,
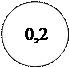
Это значит, что δо,п = ± 0,2 %.
· В документации цифрового измерительного прибора его класс точности обозначен 0,01/0,005. Это значит, что
.
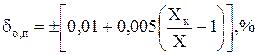Все числа, фигурирующие в обозначениях классов, выбираются из ряда
(1; 1,5; 2; 2,5; 4; 5; 6)·10а,
где а = 1; 0; – 1; – 2; …
Кроме основной погрешности класс точности даёт информацию о дополнительных погрешностях, например, так, как это было показано в приведённых выше примерах, но как именно, в частности, «…не более половины основной…» или «…не более основной…» – это надо уточнять по документации на прибор.
1.3.4. Ха
|
|
|
