Представление результатов измерений

1.5.1. Составляющие погрешности измерения.

 

Напоминание: в общем случае погрешность результата измерения не равна погрешности средства измерения, с помощью которого получен этот результат.

Составляющие погрешности измерения:

 

 

Методическая погрешность – от несовершенства самого метода измерения, она не исчезает при идеальном приборе.

Пример: измерение высоты над поверхностью земли по атмосферному давлению. Эта погрешность не исчезает при идеальном приборе для измерения давления, ибо давление зависит не только от высоты.

 

Погрешность отсчитывания. На рисунке в сильно увеличенном виде показано одно деление шкалы, т.е. расстояние между соседними метками. Будем считать, что отсчёт делают с округлением до четверти деления (иногда до половины, иногда до целого деления, но это плохо). Например, сделан отсчёт 104,25 дел. Тогда можно считать, что при любом положении стрелки погрешность округления не выходит за пределы ± 0,125 дел (расстояние от точечной линии до пунктирной). Тогда Δ_{отс, п} = ± 0,125с, где с – цена деления.

 

Пример. У прибора класса 0,5 шкала имеет 150 делений. Следовательно, предельные значения основной приведённой погрешности γ_о,п = ± 0,5 %, а предельные значения приведённой погрешности отсчитывания

 

γ_отс,п = ± 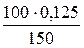= ± 0,083 %, т.е примерно от γ_о,п.

 

1.5.2. Запись результата измерения.

 

Пример 1.

 

I = (15,40 ± 0,14) A; P = 1

I = (15,400 ± 0,075) A; P = 0,95

 

В этих записях 15,40 А и 15,400 А – результат измерения; ± 0,14 А – предельные значения погрешности измерения при вероятности Р = 1; ± 0,075 А – граничные значения погрешности измерения при вероятности Р = 0,95.

Интерпретация: вероятность того, что истинное значение тока I_ист находится в интервале от 15,26 А до 15,54 А равна 1; вероятность того, I_ист находится в интервале от 15,325 А до 15,475 А равна 0,95.

 

Пример 2.

 

Граничные значения погрешности измерения вычислены и составляют ± 0,0253 В при вероятности Р = 0,95. Запись:

 

(41,535 ± 0,025) В; Р = 0,95.

 

Правила:

1) Число, выражающее предельные или граничные значения погрешности измерения, должно содержать две значащих цифры.

Пример: числа 0,14 и 0,014 имеют две, а число 0,140 – три значащих цифры.

Примечания:

а) В литературе можно встретить другие рекомендации: одна или две цифры, причём, если первая 1 или 2 (иногда ещё или 3), то две обязательно. Мы условимся: всегда две – это проще и не ухудшает.

б) В процессе вычислений надо сохранять минимум три цифры, и только в конце округлять до двух.

2) Число, выражающее результат измерения, должно оканчиваться цифрой того же разряда, что и значение погрешности.

Пример: запись (15,4 ± 0,14) А не верна, а (15,40 ± 0,14) А – верна.

3) Округление чисел, выражающих результат и погрешность измерения, надо производить по обычным правилам: если первая из отбрасываемых цифр меньше пяти, остающиеся цифры не меняются, если же она больше или равна пяти, то последняя из остающихся цифр увеличивается на единицу.

 

1.5.3. Вычисление погрешностей измерений.

 

Прямые измерения.

а) При вероятности Р = 1 находят предельные значения погрешности измерения Δ_п путём арифметического суммирования предельных значений составляющих Δ_i,п:

Δ_п = ± 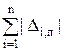. (20)

Составляющими могут быть:

– основная погрешность Δ_о,п;

– дополнительные погрешности Δ_д,п;

– погрешность отсчитывания Δ_отс,п;

– погрешность взаимодействия Δ_вз,п.

При таком способе суммирования плохо то, что получается сильное завышение погрешности, ибо очень мало вероятно, чтобы все составляющие оказались на своих пределах и были при этом одного и того же знака (плюс или минус). Зато этот способ даёт полную гарантию.

б) При вероятности Р < 1, например, при Р = 0,95, находят граничные значения погрешности измерения Δ_гр путём статистического суммирования предельных значений составляющих Δ_i,п:

 

Δ_гр = ± К . (21)

 

Значение К зависит от законов распределения случайных величин Δ_i и от задаваемого значения вероятности Р. Если законы распределения неизвестны, рекомендуется принять, что для всех составляющих это закон равномерной плотности. При этом из теории вероятностей следует, что значения К при разных значениях Р соответствуют приведённым в таблице 1:

 

Таблица 1.

Р	0,9	0,95	0,99
К	0,95	1,1	1,4

 

Значение Δ_гр может быть существенно меньше по сравнению с Δ_п, хотя Р близко к единице. Максимальное снижение Δ_гр по сравнению с Δ_п будет, если все Δ_i,п одинаковы:

Δ_i,п =А.

При Р = 1 получим

Δ_п = ± nA,

а при Р < 1

Δ_гр = ± К = ± КА ,

т.е.

=

например, при n = 4 и К = 1,1 различие между предельным и граничным значениями получается примерно в два раза.

Если, наоборот, какая-нибудь из Δ_i сильно преобладает над остальными, то

Δ_гр ≈ Δ_п.

 

Косвенные измерения.

Для вычисления погрешности мы располагаем известной функциональной зависимостью результата косвенного измерения Y от аргументов Х₁; Х₂;…Х_n:

Y = f (Х₁; Х₂;…Х_n).

Пример: R = здесь Y = R; Х₁ = U; X₂ = I.

Требуется найти погрешность ΔY, происходящую от погрешностей ΔХ₁; ΔХ₂;… ΔХ_n.

Упростим обозначения: ΔY = Δ; ΔХ₁ = Δ₁; ΔХ₂ = Δ₂;… ΔХ_n = Δ_n.

Для решения нашей задачи в математике есть т.н. «формула полного дифференциала»:

 

. (22)

 

Предельные значения Δ:

 

Р = 1. (23)

Частные случаи.

1) Y = a₁X₁ + a₂X₂ +...+a_nX_n = , т.е. Y – линейная функция аргументов Х₁; Х₂;…Х_n. В данном случае , следовательно,

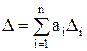и

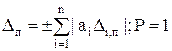. (24)

Примеры:

 

а) Y = X₁ + X₂; здесь a₁ = а₂ = 1; Δ = Δ₁ + Δ₂; Δ_п = ± (|Δ_1,п| + |Δ_2,п|); Р = 1.

б) Y = X₁ – X₂; здесь a₁ = 1; а₂ = – 1; Δ = Δ₁ – Δ₂; Δ_п = ± (|Δ_1,п| + |Δ_2,п|); Р = 1.

Итак, Δ_п для суммы и разности одинаковы.

2) Y = где а₁; а₂;…а_n – действительные числа, положительные и отрицательные, целые и дробные.

Пример: Y = ; здесь а₁ = 2; а₂ = – 0,5.

Частные производные:

Далее:

 

 

Следовательно,

Δ = Y(a₁δ₁ + a₂δ₂ +...+ a_nδ_n);

δ = .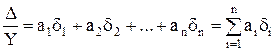

 

Предельные значения:

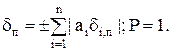(25)

Примеры:

а) Y = X₁X₂; здесь а₁ = а₂ = 1; δ = δ₁ + δ₂; δ_п = ± (|δ_1,п| + |δ_2,п|); P =1.

б) Y = здесь а₁ = 1; a₂ = – 1; δ = δ₁ – δ₂; δ_п = ± (|δ_1,п| + |δ_2,п|); P =1.

Итак, δ_п для произведения и частного одинаковы.

Объединяя наши четыре примера, можно сказать так:

 

Для суммы и разности надо суммировать предельные значения абсолютных погрешностей, для произведения и частного – предельные значения относительных погрешностей.

 

Мы рассмотрели арифметическое суммирование при Р = 1. При Р < 1 применяют статистическое суммирование:

 

, (26)

 

где К зависит от задаваемого значения вероятности Р так же, как при прямых измерениях (см. табл. 1).

Каждый может написать формулы для Δ_гр для рассмотренных выше частных случаев.

 

Пример.

Требуется определить мощность Р, выделяющуюся в резисторе с номинальным значением сопротивления R_ном = 1 кОм с предельно допускаемыми отклонениями от этого номинала ± 1,0 %. Резистор подключён к источнику напряжения постоянного тока. Параллельно резистору постоянно подключён вольтметр класса точности 0,5 с диапазоном измерения от 0 до 15 В и он показывает значение напряжения U = 6,0 В.

Решение. Р = 6²10^-3 Вт = 0,036 Вт = 36 мВт. В соответствии с (25)

δ_п = 2 δ_U,п + δ_R,п, где δ_U,п и δ_R,п – предельные относительные погрешности вольтметра и резистора. Из условия γ_R,п = ± 1,0 %, а δ_U,п = γ_U,пU_N/U = ± 0,5·15/6 = 1,25 %. Следовательно,

δ_п = ± (2·1,25 + 1,0) = ± 3,5 %; Δ_п = 0,01 δ_пР = ± 0,01·3,5·25 = ± 0,875 мВт ≈ ± 0,86 мВт.

Ответ: (36,00 ± 0,86) мВт при вероятности 1.

СТАНДАРТИЗАЦИЯ

⇐ Предыдущая12345Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: