 |
Провести оценку качества трендовой модели в целом.
|
|
|
|
Для оценки качества трендовой модели в целом необходимо рассмотреть ряд остатков – разностей значений ряда и значений тренда:
et = yt - 
.
Впервые ряд остатков составлен в таблице J, предназначенной для вычисления стандартной ошибки коэффициента b.
Для оценки качества трендовой модели проверяют следующие гипотезы:
а) о случайности ряда остатков методом поворотных точек (поворотная точка – точка экстремума, то есть точка, в которой значение элемента ряда остатков одновременно больше или меньше, чем значения в соседних точках); число таких точек d можно найти по графику ряда остатков. Среднее число точек поворота для случайного ряда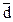 
и их дисперсия 
находятся по эмпирическим формулам:
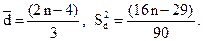
Затем вычисляют статистику 
.
Критерий принятия решения. Если 
< 1,96 (для коротких рядов), то гипотеза о случайности ряда остатков принимается и на уровне значимости 5% можно сделать вывод о том, что построенный тренд существует (высокого качества);
б) о равенстве математического ожидания ряда остатков нулю по статистике
где 
- среднее значение ряда остатков, 
- среднее квадратическое отклонение ряда остатков; на 5% уровне значимости вычисленное значение T сравнивается с критическим значением Tкр, взятым из таблицы M c (n – 1) степенями свободы:
Таблица M
Критические значения распределения Стьюдента
| k | 
| ||||||||
| Tкр | 3,18 | 2,57 | 2,45 | 2,23 | 2,16 | 2,12 | 2,09 | 2,04 | 1,96 |
Критерий принятия решения. Если вычисленное значение статистики окажется меньше критического ее значения (T < Tкр), то гипотеза о равенстве математического ожидания ряда остатков нулю принимается и модель на уровне значимости 5% считается адекватной;
|
|
|
в) об отсутствии автокорреляции ряда остатков; при этом используется критерий Дарбина-Уотсона со статистикой DW:
Если DW 
следует использовать вспомогательную статистику 
Расчетное значение DW (или 
) сравнивается с верхним D2 и нижним D1 критическими значениями статистики DW, представленными в таблице N, для различной длины ряда n и числа определяемых параметров k на уровне значимости 5% (0,05).
Таблица N
Критические значения статистики DW для различной длины ряда n и числа определяемых параметров k на уровне значимости 5%
| n | K=1 | K=2 | K=3 | |||
| D1 | D2 | D1 | D2 | D1 | D2 | |
| 0,98 | 1,34 | 0,94 | 1,52 | 0,67 | 1,72 | |
| 1,08 | 1,36 | 0,95 | 1,54 | 0,82 | 1,75 | |
| 1,35 | 1,49 | 1,28 | 1,57 | 1,21 | 1,65 |
Критерий принятия решения. Если расчетное значение статистики DW больше верхнего табличного значения D2, то гипотеза о независимости уровней остаточной последовательности, то есть об отсутствии в ней автокорреляции, принимается.
Если значение DW меньше нижнего табличного значения D1, то эта гипотеза отвергается и модель считается неадекватной.
Если же значение D находится между значениями D2 и D1, включая сами эти значения, то считается, что нет достаточных оснований сделать тот или иной вывод, и необходимы дальнейшие исследования, например, по большей выборке данных.
г) о возможности осуществления оценки соответствия тренда статистическим данным с помощью коэффициента детерминации; известно, что коэффициент детерминации R2 является суммарной мерой общего качества уравнения регрессии (его соответствия статистическим данным)
В общем случае коэффициент детерминации рассчитывается по формуле
Для этого коэффициента в общем случае справедливо соотношение 0 £ R2 £ 1.
Критерий принятия решения. Чем R2 ближе к нулю, тем слабее линейная связь между X и Y и тем менее качественным является тренд; чем ближе R2 к единице, тем эта связь значительнее и тренд качественнее.
|
|
|
Коэффициент детерминации является мерой, позволяющей определить, в какой степени найденная прямая регрессии дает лучший результат для объяснения поведения зависимой переменной Y, чем горизонтальная прямая 
.
|
|
|
