 |
Метод наименьших квадратов
|
|
|
|
Контрольная работа
По дисциплине: «Эконометрика»
Специальность: 080100
Студент:.
Шифр:
Преподаватель: Н.В. Рачёва
Санкт-Петербург
Заданиенаконтрольнуюработу
В контрольной работе студенту необходимо выполнить одну задачу, выбрав параметры.
Вариант №4
4 a0 =140; a1 =40; s=35
В контрольном задании требуется:
1. Смоделировать исходные данные.
2. Найти коэффициенты регрессии методом наименьших квадратов.
3. Проверить гипотезу о заданном в контрольном задании значении a 1 средних удельных затрат.
4. Построить доверительный интервал для значения a1 средних удельных затрат.
5. Найти коэффициент детерминации и пояснить его смысл.
6. Построить доверительный интервал для прогноза фактических затрат при объеме продаж x 0 = 6,5.
Решим пример контрольного задания для следующих значений параметров
моделирования: a0 =140; a1 =40; s=35.
Моделирование исходных данных
Пусть x обозначает объем продаж некоторого продукта (в тысячах единиц),
а y – фактические затраты на реализацию этого объема (в у. е.). Здесь объем
продаж x будем считать фактором, объясняющим фактические затраты y.
Допустим, что уравнение
y= 140 + 40 x+u (4.4)
задает зависимость фактических затрат y от объема продаж x. Случайная
величина u распределена нормально с математическим ожиданием 0 и
стандартным отклонением s= 35. Из (4.4) следует, что фактические затраты y складываются из средних затрат
y ср=140 + 40 x (4.5)
и отклонений u фактических затрат от средних затрат. Таким образом, из (4.4)
следует, что для фактических затрат y имеет место равенство
|
|
|
y = y ср+ u. (4.6)
Для получения исходных данных будем моделировать уравнение (4.6)
последовательно для объема продаж x = 1,2..,10. При заданном объеме продаж x
средние затраты вычисляем по формуле (4.5), а значения u отклонений
фактических затрат от средних будем моделировать с помощью таблицы
случайных чисел, распределенных нормально с математическим ожиданием 0 и
дисперсией 1, следующим образом. Из таблицы А приложения выбираем
любые десять значений (например, первые десять значений второго столбца).
Обозначим их zi и поместим в первый столбец табл. 4.1. По выбранным значениям zi вычислим отклонения от средних затрат ui по формуле
ui =s× zi..
В нашем примере s =35. Эти значения составят второй столбец табл. 4.2. В
третий и четвертый столбцы таблицы поместим объемы продаж xi и средние затраты yi пр, вычисленные по формуле (4.5). Тогда фактические затраты
получаются, согласно формуле (4.6), сложением средних затрат из столбца
четыре с отклонениями от них из второго столбца. Фактические затраты
помещены в пятый столбец табл. 4.2. Для примера получим фактические
затраты при объеме продаж x =1. Из (4.6) следует, что фактические затраты в
первом наблюдении равны
y 1 = y ср+ u 1=180+19,11=199,11
Заметим, что значение 19,11 означает, что фактические затраты превысили
средние затраты на 19,11 у. е. Аналогично вычисляются фактические затраты y2. Во втором наблюдении при x =2
y 2= yср+ u 2=220+(-37,905)=182,095
В этом случае фактические затраты оказались меньше средних на 37,905 у.е.
Продолжая моделирование аналогичным образом для x =3,4 ¼,10, построим
исходные данные для десяти наблюдений.
Метод наименьших квадратов
Рассчитаем теперь коэффициенты регрессии по формулам
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для этого необходимо предварительно вычислить xiyi, xi2, yi2, заполнить шестой, седьмой и восьмой столбцы таблицы, а затем найти сумму и среднее арифметическое этих столбцов. Тогда коэффициенты регрессии будут равны
|
275-256
Таким образом, уравнение регрессии имеет вид
y пр=119,2+40,69 x. (4.7)
Таблица 4.2
Уравнение регрессии (4.7) позволяет вычислить прогноз средних затрат y ср(x) при любом объеме продаж x. При x =1 средние затраты составят
y cр(1)= 180 у.е.,
а их прогноз
y пр(1)=40,69+119,2´1=159,9 у. е.
(При этом по исходным данным фактические затраты составляли 257,3 у.е.) Расхождение между фактическими и прогнозируемыми затратами называют остатками ei. При x =1 остаток составит величину
e 1=y1- y пр(1)=199,11-159,9= 39,21.
Все значения yi при остатки ei помещены в двух последних столбцах табл. 4.2. Ниже построен график линии регрессии и точками отмечены исходные данные.
График регрессии:
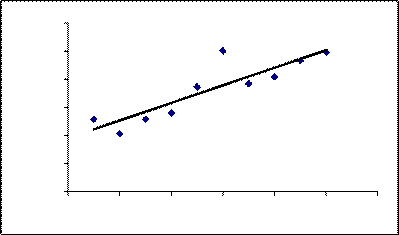600,00 y = 40,69x + 119,2 500,00
400,00
300,00
200,00
100,00
0,00
0 2 4 6 8 10 12
Для дисперсии s 2 найдем ее оценку s2 по формуле
|
|
Тогдастандартнаяошибка s =1037 =32,2.
Теперь можно сравнить параметры уравнения модели (4.4) с
коэффициентами уравнения регрессии (4.7) и стандартное отклонение s со
стандартной ошибкой s:
параметр a 0=140, а его оценка b 0=119,2 параметр a 1=40, а его оценка b 1=40,69, параметр s=35, а его оценка s =49,72.
|
|
|
