 |
Корреляционная и ковариационная функции
|
|
|
|
Широкий круг инженерных приложений теории случайных процессов связан с выявлением линейных зависимостей между двумя или более совокупностями данных. Такие линейные зависимости обычно определяются через корреляционные функции, либо через их преобразования Фурье, называемые спектральными плотностями.
Вспомним классическое определение корреляционной функции, известное из курса статистики.
Пусть в некотором эксперименте получены два множества результатов измерений:
, 
, 
,
где – например, нагрузка, приложенная к конструкции;
– вызванное ею напряжение;
– общее количество измерений.
Измерения, проведенные при различных значениях нагрузки, приведут к зависимостям типа показанных на рисунке 1.12.
В идеальном случае измерения дают точную линейную зависимость между 
и 
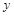(рисунок 1.12, а). Неправильная постановка эксперимента может привести к другой крайности, когда между нагрузкой и напряжением отсутствует какая-либо связь (рисунок 1.12, б). Возможны зависимости и промежуточного вида. На рисунке 1.12, в угадывается линейная связь между и 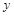, но точного аналитического выражения для нее записать нельзя из-за случайного характера этой связи или ошибок измерений. На рисунке 1.12, г между и 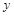существует точная аналитическая зависимость, но она нелинейна.
а) линейная корреляция; б) отсутствие корреляции
в) умеренная линейная корреляция; г) нелинейная корреляция
Рисунок 1.12 – Различные степени корреляции
Меру линейности связи и 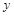можно задать как усредненное произведение разностей 
и 
. Если размер выборки стремится к бесконечности, то предел этого усредненного произведения определяет корреляцию между и :
|
|
|
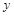. (1.24)
Наибольшее возможное значение корреляции двух случайных величин определяется равенством
,
поэтому в качестве меры коррелированности обычно используют отношение
, 
. (1.25)
Величину 
называют коэффициентом корреляции, который характеризует меру линейной зависимости между двумя переменными и .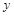
Пусть теперь интересующие нас данные являются результатами измерения двух случайных процессов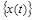 
, 
, которые предполагаются стационарными и эргодическими, так, что их можно описать индивидуальными реализациями. Понятие корреляции случайных процессов вводят, используя дополнительную переменную – временной сдвиг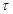 
между процессами, или запаздывание относительно .
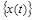Взаимная корреляционная функция двух случайных процессов для произвольного сдвига 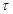вводится по соотношению
. (1.26)
Для стационарных СП справедливо выражение
, (1.27)
где 
– взаимная ковариационная функция двух процессов.
Случайные процессы считаются некоррелированными, если их взаимная корреляционная функция равна нулю.
Согласно (1.27) взаимные корреляционная и ковариационная функции двух случайных процессов совпадают, если средние значения обоих процессов равны нулю.
В частном случае, когда случайные процессы совпадают =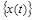
= , связь между корреляционной и ковариационной функциями принимает вид
, (1.28)
где 
– ковариационная функция процесса 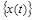, определяемая как
. (1.29)
Свойства ковариационной и корреляционной функций стационарного СП, согласно выражениям (1.19), (1.28), (1.29), определяются следующими соотношениями:
1. 
, 
, 
;
2. 
, 
, 
.
Рисунок 1.13 иллюстрирует свойства ковариационной функции.
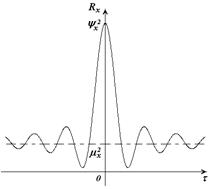
Рисунок 1.13 – Типичная ковариационная функция
С увеличением временного сдвига 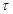функция корреляции случайного процесса стремится к нулю:
при 
.
Чем быстрее убывает эта функция, тем меньше оказывается статистическая связь между мгновенными значениями случайного процесса в два различных момента времени. Числовой характеристикой, служащей для оценки скорости изменения реализаций случайного процесса, является интервал корреляции:
|
|
|
. (1.30)
Если известна информация о поведении какой-либо реализации случайного процесса в прошлом, то возможен вероятностный прогноз его значений на время порядка 
. Попытка прогнозирования на время, существенно превышающее интервал корреляции, окажется безрезультативной, поскольку мгновенные значения случайного процесса, существенно удаленные друг от друга по времени, практически некоррелированы.
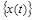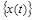По аналогии с коэффициентом корреляции для двух случайных величин вводят понятие нормированной корреляционной функции, определяющей степень линейной зависимости двух случайных процессов и при временном сдвиге процесса относительно на величину :
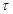, (1.31)
причем 
для всех .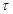
Взаимная ковариационная функция двух процессов применяется во многих важных практических случаях.
Определение времени задержки. Предположим, что нас интересует вопрос о том, какое время необходимо для того, чтобы сигнал прошел через данную систему. Если система линейна, то, зная взаимную ковариационную функцию, связывающую сигналы на входе и выходе системы, можно определить интересующее время запаздывания, поскольку среднее значение произведения двух линейно связанных сигналов достигает максимума, когда сдвиг во времени между ними равен нулю.
Так как сигнал на выходе системы смещен во времени относительно сигнала на входе, их взаимная ковариационная функция будет иметь максимум при значениях сдвига, равном времени, которое необходимо для прохождения сигнала через данную систему.
Определение тракта сигнала. Рассмотрим линейную систему, через которую сигнал может проходить двумя или более различными трактами и давать на выходе наблюдаемый сигнал. Предположим, что нас интересует определенный тракт в системе.
Например, при работе мощных машин на заводе часто могут возникать нежелательные шум и вибрация в прилегающих к заводу административных зданиях, причем энергия может передаваться несколькими путями – через строения или акустическим образом по воздуху. Чтобы эффективно бороться с шумом и вибрацией, необходимо точно определить путь прохождения сигнала.
|
|
|
Вопросы такого рода можно решать с помощью взаимной ковариационной функции, связывающей сигналы на входе и выходе рассматриваемой системы. Каждому тракту в системе обычно соответствует определенное время задержки, поэтому на взаимной коррелограмме для трактов, которые дают значимый вклад в энергию сигнала на выходе, появляются отдельные максимумы. Если вычислить предполагаемое время запаздывания, связанное с различными трактами, и затем полученные данные сравнить с измеренными значениями сдвига, соответствующими положению максимумов на взаимной коррелограмме, то можно найти тракты, которые дают наибольший вклад в энергию сигнала на выходе.
|
|
|
