 |
Идентификация объекта управления
|
|
|
|
В современных сложных объектах, как правило, выходной сигнал объекта зависит не от одного входного сигнала, как в случае с кривой разгона, а от нескольких входных сигналов, т.е. объект управления имеет сложное переплетение взаимосвязей входных и выходных сигналов.

Рис. 1. Схема объекта, состоящего из нескольких взаимосвязанных входных-выходных сигналов
Для идентификации таких сложных объектов используется метод регрессионного анализа с проведением активного эксперимента на базе теории математического планирования эксперимента.
Назначение этой теории – значительно сократить количество экспериментальных опытов и упростить расчеты, необходимые для получения уравнения взаимосвязи выходного сигнала с несколькими входными сигналами – уравнения регрессии.
Сокращение числа необходимых экспериментов в теории математического планирования эксперимента достигается за счет одновременного изменения всех входных сигналов (факторов), а упрощение расчетов получается за счет того, что изменение входных сигналов (факторов) нормируется, т.е. величины 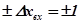 . Пусть
. Пусть 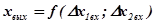 – зависит от 2-х входных факторов.
– зависит от 2-х входных факторов.

Рис. 2. Схема исследования объекта методом регрессионного анализа для двух входных сигналов (факторов)
Точка О – номинальный режим работы объекта. Нормализация происходит за счет того, что начало координат переносится в точку О на  .
.

Рис. 3. Схема центрального плана полного факторного эксперимента для двух входных сигналов (факторов)
Здесь (рис. 3) изображен план проведения опытов для изучения зависимости  . Число опытов равно 4=22 – полный факторный эксперимент; Для k входных факторов число опытов в факторном эксперименте: N=2k. При k=3 N=8; k=4, N=16 и т.д.
. Число опытов равно 4=22 – полный факторный эксперимент; Для k входных факторов число опытов в факторном эксперименте: N=2k. При k=3 N=8; k=4, N=16 и т.д.
|
|
|
На приведенном выше рис. 3. изображен центральный (точка О – в центре) ортогональный полный факторный план эксперимента для 2-х входных факторов.
Таблица 1. Полный факторный эксперимент для k=2.
| № опыта | 
| 
| 
|
| 1 | +1 | +1 | 
|
| 2 | -1 | +1 | 
|
| 3 | -1 | -1 | 
|
| 4 | +1 | -1 | 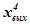
|
Свойство плана, когда, называется ортогональностью плана.
Таблица 2. Полный факторный эксперимент для k=3.
| № опыта | 
| 
| 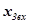
| 
|
| 1 | +1 | +1 | +1 | 
|
| 2 | -1 | +1 | +1 | 
|
| 3 | -1 | -1 | +1 | 
|
| 4 | +1 | -1 | +1 | 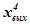
|
| 5 | +1 | +1 | -1 | 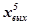
|
| 6 | -1 | +1 | -1 | 
|
| 7 | -1 | -1 | -1 | 
|
| 8 | +1 | -1 | -1 | 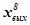
|
В полном факторном плане экспериментов число опытов резко возрастает в зависимости от числа входных факторов: k=4 N=16; k=5, N=32; k=6, N=64 опыта. Поэтому для сокращения числа опытов с минимальной потерей информации применяются сокращенные планы – дробные реплики. Если планы содержат половину опытов полного факторного эксперимента, то такой план носит название полуреплики.
Таблица 3. Пример полуреплики для k=4 (ПФЭ=16)
| № опыта | 
| 
| 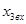
| 
|
| 1 | +1 | +1 | +1 | +1 |
| 2 | +1 | -1 | +1 | -1 |
| 3 | -1 | +1 | +1 | -1 |
| 4 | -1 | -1 | +1 | +1 |
| 5 | +1 | +1 | -1 | -1 |
| 6 | +1 | -1 | -1 | +1 |
| 7 | -1 | +1 | -1 | +1 |
| 8 | -1 | -1 | -1 | -1 |
Используют также ¼ реплики от полного факторного эксперимента.
Уравнение взаимосвязи входного и выходного сигналов – уравнение регрессии – записывается в виде алгебраического полинома 1-ой и 2-ой степени в следующем виде:
1-ой степени:
xвых = b0 +b1x1+b2x2;
с учетом взаимодействия входных факторов для 2-х входных факторов x1 и x2:
xвых = b0 + b1x1 + b2x2 + b12x1 x2.
Полином второй степени – уравнение регрессии:

Естественно, это уравнение более точно описывает взаимосвязь xвых – функции отклика – с входными факторами (сигналами) объекта.
Задача идентификации объекта управления (ОУ) методом регрессивного анализа сводится к выбору порядка математической модели – уравнения регрессии – и определению коэффициентов b0, b1, b2, b12 и т.д. в этом уравнении регрессии. При определении этих коэффициентов используется метод наименьших квадратов, в котором определяется наименьшая сумма отклонений в квадрате (2-ой степени) между реально полученным в эксперименте выходным сигналом и выходным сигналом, рассчитанным (предсказанным) по уравнению регрессии, т.е. ищут минимум функции:
|
|
|

Минимум функции Ф достигается в том случае, когда первая частная производная (тангенс угла наклона к впадине) равна нулю, т.е.
 .
.
Пример

Рассмотрим пример использования метода наименьших квадратов. Пусть выходной сигнал (функция отклика) зависит от одного фактора (входного сигнала). Активно проведено n экспериментов. Задана  и получена
и получена  – результатов экспериментов. Общий вид уравнения регрессии 1-го порядка для примера:
– результатов экспериментов. Общий вид уравнения регрессии 1-го порядка для примера:
xвых = b0 + b1x1
Методом наименьших квадратов ищем минимум функции Ф:

Для получения минимума этой Ф приравниваем к нулю частные производные
 .
.
Для удобства получения частных производных введем фиктивную переменную x0=1 и функцию Ф запишем:


x0=1 можно убрать. Тогда

Решая эту систему алгебраических уравнений (можно методом Крамера), находим:

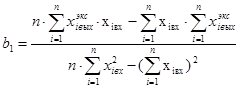
Проверка идентичности математической модели – уравнения регрессии исследуемого объекта проводится по нескольким критериям адекватности и идентичности модели.
Поскольку результаты опытов в эксперименте заранее точно предсказать невозможно, то обработка и сами результаты связаны с неопределенностью или вероятностью. Вероятность изменяется в пределах: 0 – события быть не может, 1 – событие произойдет обязательно (день-ночь). При большом числе параллельных (одинаковые условия) опытов вероятность может быть задана в виде функции распределения вероятностей (рис. 4.):

Рис. 4. Схема нормального (гауссовского) закона распределения вероятностей
На практике чаще всего используется так называемое нормальное (гауссовское) распределение вероятностей.
Случайная величина ( ) имеет несколько числовых характеристик, наиболее важные из которых – это математическое ожидание и дисперсия.
) имеет несколько числовых характеристик, наиболее важные из которых – это математическое ожидание и дисперсия.
Математическое ожидание – это среднее взвешенное значение случайной величины
|
|
|

Дисперсия характеризует разброс значений случайной величины относительно ее математического ожидания.
 .
.
Проверка значимости уравнения регрессии проводится по критерию Фишера или F-критерию. Проверка заключается в определении, значимо ли (больше ошибки измерения) полученное уравнение  отличается от уравнения
отличается от уравнения  . Для этого вычисляют дисперсию относительно среднего значения выходного сигнала:
. Для этого вычисляют дисперсию относительно среднего значения выходного сигнала:
 ,
,
где f1 – число степеней свободы,
 .
.
А также остаточную дисперсию:
 ,
,
f2 – число степеней свободы.
Величину критерия Фишера (F-критерий) определяют по формуле:
 (должно быть).
(должно быть).
Значимость коэффициентов bi уравнения регрессии определяют по t-критерию (критерии Стьюдента):
 ,
,
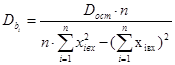 .
.
|
|
|
12 |


