вблизи проводящей плоскости

электромагнитное поле

Силовое воздействие поля на электрические заряды и токи положено в основу определения основных векторных величин, которыми характеризуют поле: напряженности электрического поля E и индукции магнитного поля B.

1. Напряженность электрического поля – физическая характеристика электрического поля, определяющая силовое воздействие поля на неподвижный электрический заряд.

Напряженность электрического поля является векторной величиной, численно равной отношению силы , с которой электрическое поле действует на положительный заряд q, внесенный в рассматриваемую точку поля, к значению этого заряда, когда величина заряда стремится к нулю

Сила электрического поля, действующая на заряд, направлена вдоль вектора . Линия напряженности электрического поля – это линия, в каждой точке которой вектор направлен по касательной к ней.

Под действием электрического поля происходит поляризация вещества т.е. ориентация диполей относительно векторов поля. Поляризация – это сумма всех дипольных моментов вещества, отнесенная к единице объема

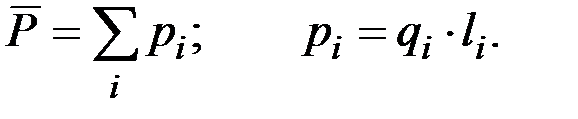
Поляризация показывает, насколько вектор электрического смещения индукции в данной среде отличается от вектора электрического смещения в вакууме.

 

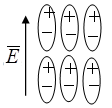
Рис.1.1

Если среда состоит из заряженных частиц (диполей), выстраивающихся по направлению приложенного электрического поля, то поляризация называется ориентационной (рис.1.1). Если среда состоит из нейтральных (в электрическом отношении) частиц, то происходит электронная поляризация, т.е. вытягивается электронная оболочка атомов. В любом случае

где ε ₀ = 1/36 π ∙10^-9 Ф/м = 8,85 пФ/м – электрическая постоянная;

χ _э – электрическая восприимчивость;

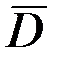– вектор электрического смещения:

где(1+ χ _э) = ε_r

ε_r – относительная электрическая проницаемость;

ε = ε ₀ ε_r – абсолютная электрическая проницаемость;

– материальное уравнение для векторов электрического поля.

 

2. Магнитная индукция – это физическая характеристика магнитного поля, определяющая силовое воздействие на движущийся заряд.

Магнитная индукция – векторная величина, характеризующая магнитное поле в каждой его точке.

Численно магнитную индукцию поля можно определить по механической силе, действующей на движущийся заряд, либо на элемент проводника с током:

Направление силы находят по правилу векторного произведения

(). Механическая сила максимальна, если вектор скорости v перпендикулярен вектору индукции B.

Для заряда q, движущегося со скоростью v во внешнем поле:

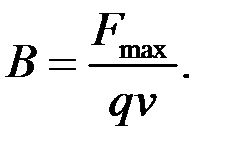
С вектором магнитной индукции напряженность магнитного поля 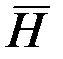связана соотношением:

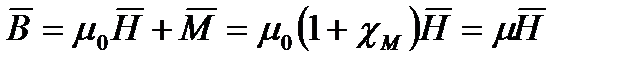
где μ = μ₀ μ_r – абсолютная магнитная проницаемость,

μ₀ = 4 π ∙10^-7 Гн/м – магнитная постоянная,

μ_r = (1 + χ_M) -– относительная магнитная проницаемость,

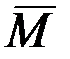– намагниченность, равная сумме магнитных моментов атомов в единице объема вещества:

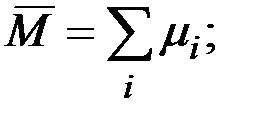
Намагниченность пропорциональна напряженности приложенного поля:

где χ_М – магнитная восприимчивость. _.

 

1.3. Виды плотности тока

Электрический ток создает магнитное поле как составную часть

электромагнитного поля. Различают токи проводимости, смещения и

переноса.

1. Вектор плотности тока проводимости

образуется движением зарядов в проводящей среде под действием постоянного или переменного во времени поля напряженностью . Он сопровождается выделением тепла по закону Джоуля-Ленца.

2. Вектор плотности тока переноса

образуется заряженными телами и частицами, движущимися в непроводящей среде или в вакууме со скоростью .

3. Вектор плотности тока смещения

наблюдается только в переменном во времени поле.

6. Вектор плотности полного тока

при

Линии плотности полного тока всегда замкнуты

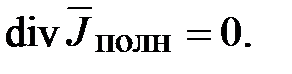
Общим свойством для всех видов тока является создание магнитного поля.

Классификация сред.

Классификация сред проводится в зависимости от поведения макроскопических параметров ε, μ, σ.

По зависимости ε, μ, σ от координаты среды делятся на однородные и неоднородные.

Если макроскопические параметры среды не зависят от координаты, то среда однородная.

Макроскопические параметры ε, μ, σ в большинстве случаев можно считать не зависящими от величины векторов поля. Материальные уравнения оказываются при этом линейными. Соответственно этому употребляется выражение «линейные среды». Однако существуют и имеют важное техническое значение среды, отличающиеся заметной зависимостью макроскопических параметров от векторов поля. Их называют «нелинейными». В электротехнике, как известно, распространены ферромагнетики – вещества, магнитная проницаемость которых значительно и сложным образом зависит от магнитного поля. Им аналогичны сегнетоэлектрики, обладающие сходной зависимостью диэлектрической проницаемости от электрического поля. Нелинейность ряда сред проявляется в сильных полях.

До сих пор говорилось лишь о так называемых изотропных средах, свойства которых одинаковы для полей любых направлений.

Однако существуют среды, проявляющие разные свойства в зависимости от направления поля, они называются анизотропными.

Разделим также среды на проводники и диэлектрики. Для такого разделения сред необходимо ввести определенный критерий.

Идеальным проводником назовем среду, в которой существует только ток проводимости, а в идеальном диэлектрике существует только ток смещения. Для реальных сред эти условия отображаются следующими неравенствами:

если то среда – реальный проводник, если – реальный диэлектрик.

 

Вопросы для самопроверки

1. Что изучает теория электромагнитного поля?

2. Назовите свойства и особенности электромагнитного поля.

3. Какие величины характеризуют электромагнитное поле?

4. Как можно графически представить электрическое поле двух зарядов?

5. Что называют точечным зарядом?

6. Как определяют напряженность поля, созданного несколькими зарядами?

7. Укажите размерности величин, характеризующих электромагнитное поле.

 

 

1.4.Основные уравнения Максвелла и их физический смысл

1.4.1.Закон полного тока

Закон полного тока в интегральной форме устанавливает связь между электрическим током и напряженностью магнитного поля и формулируется следующим образом.

Циркуляция напряженности магнитного поля по любому замкнутому контуру равна полному току сквозь поверхность, ограниченную этим контуром:

.

Полный ток равен алгебраической сумме токов проводимости, смещения и переноса:

.

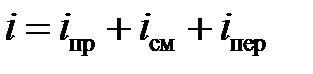В соответствии с вышесказанным плотность полного тока в произвольной среде описывается следующим соотношением:

,

а полный ток характеризуется выражением

.

С учетом этого обобщенный закон полного тока примет вид:

.

Левую часть уравнения преобразуем по теореме Стокса:

.

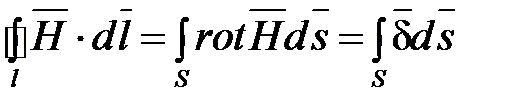Отсюда имеем дифференциальную форму закона полного тока:

 

,

где .

Физическое содержание закона полного тока - магнитное поле порождается не только движущими зарядами (ток проводимости и ток переноса), но и изменяющимся электрическим полем (плотность тока в вакууме):

.

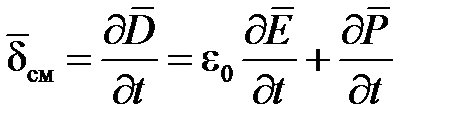Возьмем операцию div от левой и правой части выражения закона полного тока:

.

Из математики известно, что divrot º 0. Отсюда получаем уравнение непрерывности линий вектора плотности тока:

.

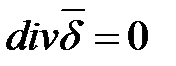Подставив в это уравнение выражение плотности тока, получим закон сохранения заряда в дифференциальной форме:

.

Полученное уравнение показывает, что в переменном электромагнитном поле токи и заряды связаны и не могут задаваться независимо друг от друга.

 

1.4.2. Закон электромагнитной индукции

Закон электромагнитной индукции, или закон Фарадея, формулируется следующим образом.

Электродвижущая сила, возникающая в контуре при изменении магнитного потока сквозь поверхность, ограниченную этим контуром, равна скорости изменения потока, взятой со знаком "минус", т.е.

, (1.1)

где электродвижущая сила определяется как

, (1.2)

магнитный поток записывается в виде

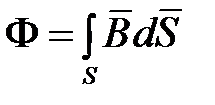. (1.3)

Закон электромагнитной индукции определяет связь электрического поля с изменяющимся во времени магнитным полем.

С учетом (1.1), (1.2) и (1.3) закон можно представить в форме

. (1.4)

Левая часть уравнения (4) преобразуем по теореме Стокса: .

Отсюда имеем дифференциальную форму закона электромагнитной индукции

.

Физическое содержание закона электромагнитной индукции: любое изменение магнитного поля во времени вызывает возникновение в той же точке пространства связанного с ним поля электрического.

Из совместного анализа 1-го и 2-го уравнений Максвелла следует вывод, переменное электрическое и переменное магнитное поля должны рассматри­ваться как два связанных проявления единого электромагнитного процесса.

Электромагнитным полем называется сово­купность взаимносвязанных и обуславливающих друг друга электрического и магнитного полей.

 

1.4.3. Принцип непрерывности магнитной индукции

 

В интегральной форме.

 

Поток вектора магнитной индукции сквозь любую замкнутую поверхность 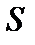равен нулю:

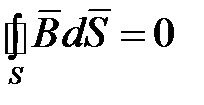, (1.5)

где для однородных изотропных сред

;

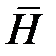– напряженность магнитного поля; – абсолютная магнитная проницаемость среды; 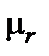– относительная магнитная проницаемость среды; – магнитная постонная.

Перейдем к дифференциальной форме записи уравнения (1.5), используя теорему Остроградского–Гаусса:

.

Отсюда имем принцип непрерывности магнитной индукции в дифференциальной форме:

.

Физическое содержание принципа заключается в том, что не существует магнитных зарядов.

 

1.4.4. Теорема Гаусса (постулат Максвелла)

Поток вектора электрической индукции (вектора электрического смещения) 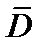сквозь произвольную замкнутую поверхность 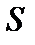равен алгебраической сумме свободных зарядов, расположенных в объеме, ограниченном этой поверхностью (рис. 1.2):

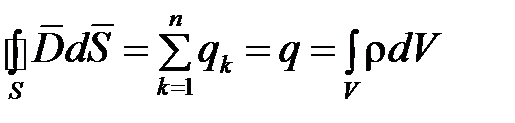, (1.6)

 

где – k -й дискретный свободный заряд, расположенный внутри объема; – полный (суммарный) свободный заряд внутри объема; 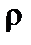– объемная плотность свободного заряда (для случая его непрерывного распределения).

Физический смысл теоремы Гаусса заключается в следующем. Если поток вектора 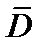через замкнутую поверхность 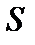не равен нулю, то внутри объема, ограниченного этой поверхностью, заключены источники данного вектора. Иными словами, источниками вектора 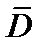являются свободные заряды. Если зарядов внутри поверхности нет, то поток вектора 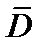сквозь такую поверхность равен нулю.

Геометрический смысл: линии вектора электрической индукции 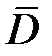связаны со свободными зарядами. Они начинаются на свободных зарядах и заканчиваются на них.

 

 

 

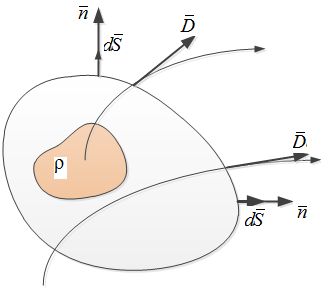
Рис.1.2

Теорему Гаусса, Максвелл обобщил (постулировал) и на переменные электрическое поля.

Левую часть уравнения (1.6) преобразуем по теореме Остроградского-Гаусса:

.

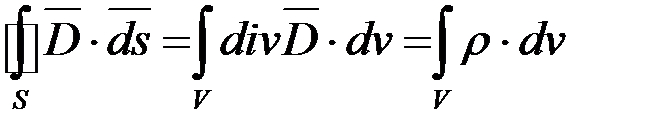Отсюда имеем теорему Гаусса в дифференциальной форме (постулат Максвелла в общем случае):

.

Четвертое уравнение Максвелла устанавливает истоки линий элек­трического поля. Оно гласит, что линии вектора электростатической индукции могут иметь разрыв, т.е., начинаться на положительных зарядах и заканчиваться на отри­цательных

1.4.5. Система уравнений Максвелла

 

Система уравнений Максвелла, наиболее полно и точно (насколько это известно) описывает все проявления электромагнитного поля, в них заключена вся электродинамика.

Уравне­ния Максвелла в дифференциальной форме:

, , , .

Материальные уравне­ния:

, , .

Здесь 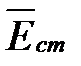- вектор стороннего электрического поля (внутри источников электрической энергии).

 

1.5.Энергия электромагнитного поля. Теорема Умова-Пойтинга

 

Энергия электромагнитного поля.

Плотность энергии электрического поля определяется как

.

Плотность энергии магнитного поля имеет вид

.

Плотность энергии электромагнитного поля может быть представлена как

.

Энергия электромагнитного поля 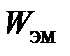в объеме

,

Для однородных изотропных сред (, , ) имеем:

,

,

что при подстановке в (3.31) дает

.

Вектор Пойнтинга.

Векторное произведение 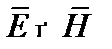обозначим через 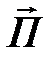Вектор называют вектором Пойнтинга, он одновременно характеризует электрическое и магнитное поля и имеет размерность поверхностной плотности мощности – 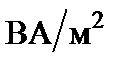. Вектор Пойнтинга образует с векторами и правую тройку, или правоходовую систему (рис.1.3).

 

Рис.1.3

 

Теорема Умова-Пойтинга математически выражает закон сохранения энергии в электромагнитном поле. Теорема представляет собой своеобразное уравнение энергетического баланса в теории поля подобно уравнению баланса мощностей в электрических цепях.

Выделим в переменном электромагнитном поле некоторый объем V, ограниченный поверхностью S. Внутри выделенного объема могут оказаться час­тично или полностью ис­точники и приемники электрической энергии в любых сочетаниях. Будем считать среду однородной и изотропной. Электромагнитное поле внутри объема описывается системой уравнений Максвелла:

, (1.7)

, (1.8)

. (1.9)

Здесь - вектор стороннего электрического поля (внутри источников электрической энергии).

Умножим скалярно уравнение (1.7) на , уравнение (1.8) на , и вычтем почленно ле­вые и правые части уравнений:

.

Из курса математики известно, что

Преобразуем правые части уравнения. Из закона Ома (1.9) следует:

;

.

После преобразования получим:

Проинтегрируем все члены полученного уравнения по выделенному объ­ему V:

Исследуем каждое слагаемое уравнения. По теореме Остроградского-Гаусса:

,

где - вектор Пой­нтинга [Вт/м ], численно равный плотности потока мощности в рассматриваемой точке;

- мощность тепловых потерь или потребляемая мощ­ность в заданном объеме, эта мощность всегда положительна;

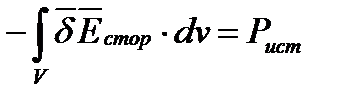- мощность источников энергии внутри объема, эта мощность от­рицательна, если векторы и 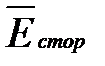совпадают, и положительна, если эти векторы не совпа­дают;

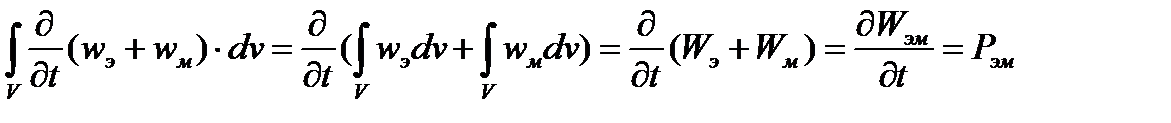- мощность элек­тро­магнитного поля, она положительна, если идет процесс накопления энергии в объеме, и от­рицательна, если идет процесс возврата энергии.

Таким образом, после принятых обозначений теорема Умова-Пойтинга получит вид:

.

Формулировка теоремы Умова-Пойтинга:

небаланс мощности в заданном объеме V компенсируется потоком вектора Пойнтинга, направленным внутрь объема (знак -) че­рез замкнутую поверхность S, ограничивающую этот объем.

Вектор Пойнтинга характеризует величину и направ­ление энергии, проходя­щей в единицу времени через единицу площади в на­правлении вектора Пойнтинга.

Теорема Умова–Пойнтинга имеет большое прикладное значение, поскольку позволяет получить информацию о процессе передачи энергии от источника к приемнику.

 

1.6.Частные виды электромагнитных полей

1.Статические поля:

электростатическое поле - создается неподвижными заряженными телами;

магнитостатические поля - поля постоянных магнитов.

2.Стационарные поля:

2.1. Электрическое поле постоянного тока (стационарное электрическое поле) образуется внутри и вне проводников при прохождении по ним постоянного тока. При этом внутри однородного проводника отсутствует объемная плотность заряда, т.е. div = 0.

2.2. Магнитное поле постоянного магнитного потока.

Магнитное поле постоянного потока и электрическое поле постоянного тока могут рассматриваться независимо друг от друга.

3.Квазистационарные поля ().

4.Общий случай.

 

Вопросы для самопроверки

1. Объясните физический смысл уравнений Максвелла.

2.Какой формулой может выражаться индукция магнитного поля?

а) B = iB ₀e^{- αx} ; б) B = iax+jby; в) B = iax;г) B = iax-jby;

где: i, j- орты осей.

 

3.Под индукцией В, входящей в правую часть второго уравнения Максвелла следует понимать:

а)индукцию стороннего поля; б) индукцию индуцированного поля;

в) индукцию токов электрического смещения;

г) индукцию от стороннего и индуктированного полей.

 

4. Отсутствие магнитных зарядов в природе следует из формулы:

; б) ; с) ; г) ;

4.Закон электромагнитной индукции в интегральной форме:

а) ; б) ;

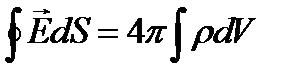с) ; г) .

 

5. div( B /μ₀) равна:

а) плотности молекулярных токов j_м;

б) плотности тока проводимости j;

в) j+j_м;

г) 0.

 

6.Теорема Гаусса в дифференциальной форме имеет вид …

а) div B = 0; б;) div H = 0;в) div D =ρ;г) ro t H =0.

7.Стационарное магнитное поле – поле, создаваемое …

1) постоянными токами;

2) электрическими зарядами любого вида;

3) постоянными зарядами и токами;

4 ) неизменными во времени неподвижными зарядами.

8. div D равна:

а) объемной плотности связанных зарядов ρ_св;

б) объемной плотности свободных зарядов ρ;

в) ρ+ρ_св ;

г) поверхностной плотности свободных зарядов.

 

 

2.Электростатическое поле

 

Электростатическое поле представляет собой частный вид электромагнитного поля. Оно создается совокупностью электрических зарядов неподвижных в пространстве по отношению к наблюдателю и неизменных во времени.

Электростатическому полю присуща способность воздействвать на помещенный в него электрический заряд с механической силой, прямо пропорциональной величине этого заряда.

2.1. Закон Кулона

 

Электростатическое поле – это поле, не изменяющееся во времени. Электростатическое поле является частным случаем электромагнитного поля. Электростатическое поле создается совокупностью электрических зарядов, неподвижных в пространстве по отношению к наблюдателю и неизменных во времени.

Основным законом электростатики является закон Кулона, математически определяющий силу взаимодействия двух неподвижных точечных зарядов.

Закон Кулона: между двумя покоящимися точечными зарядами q₁ и q₂ действует сила, прямо пропорциональная произведению зарядов и обратно пропорциональная квадрату расстояния между ними. Сила направлена по прямой от одного заряда к другому.

где – единичный вектор, направленный по прямой от положительного заряда к отрицательному заряду; r – расстояние между зарядами.

Напряженность электростатического поля можно определить как силу, действующую на единицу заряда.

По закону Кулона можно определить величину напряженности электростатического поля, создаваемого уединенным точечным телом с зарядом q в некоторой точке, отстоящей от этого тела на расстоянии r:

.

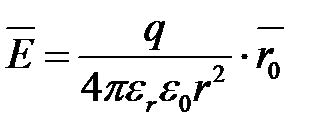Здесь ε_r – относительная диэлектрическая проницаемость среды;

(Ф/м)- электрическая постоянная;

- единичный радиус-вектор, на­правленный по радиусу от заряда, если q > 0, и к заряду, если q <0.

 

В линейных средах выполняется принцип наложения.

Принцип наложения (суперпозиции): если поле создается несколькими точечными зарядами, то общая напряженность электрического поля в любой точке равна геометрической сумме напряженностей от каждого заряда в отдельности,

,

где – напряженности в заданной точке, возбуждаемые точечными зарядами 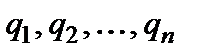(рис. 2.1). Длина вектора определяется по формуле

.

Если электростатическое поле создается системой распределенных в про­странстве за­рядов, то эти заряды разбиваются на элементарные точечные за­ряды dq, а операция сложения заменяется интегрированием по объему, площади или длине, в зависимости от того, как рас­пределены заряды в пространстве.

 

 

2.2.Уравнения электростатического поля в интегральной и дифференциальной форме

 

Для электростатического поля имеем:

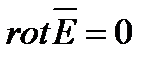или .

или , .

Ротор вектора характеризует его вихри в пространстве. Равенство озна­чает, что электростатическое поле является безвихревым, т.е. потенциальным.

В декартовой системе координат операция записыватся так:

.

- интегральная форма записи теоремы Гаусса в обобщенной форме гласит, что поток вектора элек­трического смещения сквозь замкнутую поверхность S равен ал­гебраической сумме сво­бодных зарядов, расположенные внутри поверхности S.

Для однородной среды , тогда .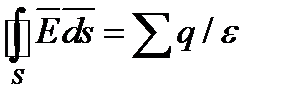

По теореме Остроградского перейдем к дифференциальной форме урав­нения теоремы Гаусса:

― дифференциальная форма теоремы Гаусса.

Дивергенция вектора характеризует его истоки в пространстве, следо­вательно, ли­нии вектора начинаются на положительных зарядах и заканчиваются на отрицательных.

Истоком вектора в отличие от истока вектора являются не только свободные ρ, но и связанные заряды .

В декартовой системе координат операция div запишется так:

.

Для однородной среды , тогда .

 

2.3. Электрический потенциал

 

Равенство озна­чает, что электростатическое поле является безвихревым, т.е. потенциальным. Учитывая, что

,

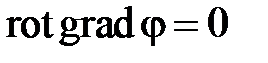приходим к следующему выводу, что для электростатического поля можно найти некоторую скалярную функцию такую, что

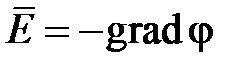. (2.1)

Скалярная функция 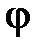называется потенциальной функцией, или просто потенциалом.

Потенциал можно выразить через напряженность электростатического поля с точностью до постоянной:

. (2.2)

Запишем формулу, определяющую напряжение между двумя произвольными точками поля а и p:

. (2.3)

Напряжение между двумя произвольными точками равно работе (энергии), затраченной полем на перемещение единичного положительного заряда из одной точки в другую.

В потенциальном поле напряжение равно разности потенциалов.

Полагая потенциал некоторой фиксированной точки p поля равным нулю (), получим:

.

Потенциал некоторой точки есть работа (энергия), затрачиваемая полем на перемещение единичного положительного заряда из данной точки в фиксированную точку, где потенциал принят равным нулю

. (2.4)

В электротехнике за базовую точку с заданным нулевым потенциалом принимают “землю”, а при отсутствии заземления - любую точку.

Потенциал является энергетической характеристикой поля.

Напряженность электрического поля определяется как градиент потенциала

где - оператор пространственного дифференцирования.

2.4.Картина поля.

 

Электрическое поле можно наглядно характеризовать совокупностью силовых и эквипотенциальных линий.

Силовая линия – это мысленно проведенная в поле линия, начинающаяся на отрицательно заряженном теле. Проводится она таким образом, что касательная к ней в любой точке ее дает направление напряженности поля в этой точке. Вдоль силовой линии передвигался бы весьма малый положительный заряд, если бы он имел возможность свободно перемещаться в поле и если бы он не обладал инерцией.

 

 

В электрическом поле могут быть проведены эквипотенциальные (равнопотенциальные) поверхности. Под эквипотенциальной поверхностью понимают совокупность точек поля, имеющих один и тот же потенциал. Если мысленно рассечь электростатическое поле какой-либо секущей плоскостью, то в полученном сечении будут видны следы пересечения плоскости с эквипотенциальными поверхностями. Их называют эквипотенциальными линиями (или эквипотенциалями).

Эквипотенциальные и силовые линии в любой точке поля пересекаются под прямым углом. На рисунке для примера изображены два заряженных тела и проведено несколько силовых и эквипотенциальных линий.

 

 

2.5.Потенциал заданного распределения заряда

Напряженность электростатического поля, создаваемого точечным зарядом q в некоторой точке, отстоящей от этого тела на расстоянии r определяется выражением (из закона Кулона):

.

Определим потенциал поля точечного заряда. Подставляя напряженность поля точечного заряда в (2.2), получим

,

.

Пусть фиксированная точка находится на бесконечности, т. е.

,

тогда постоянная интегрирования в выражении равна нулю:

.

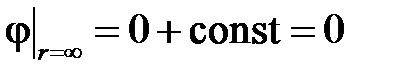В этом случае формула для потенциала произвольной точки поля точечного заряда примет вид

.

Для потенциалов, как и для напряженностей, справедлив принцип наложения (суперпозиции):

Потенциал поля n неподвижных точечных зарядов равен:

.

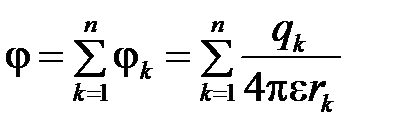В случае непрерывного распределения заряда с учетом имеем:

– для объемного распределения заряда,

– для поверхностного распределения,

– для линейного распределения заряда.

При решении задач электростатики обычно рассчитывается потенциал в точках поля, а затем определяется напряженность в этих точках.

 

 

2.5.1.Потенциал и напряженность электрического поля диполя

 

Рассмотрим систему из двух разноименных, но равных по абсолютной величине точечных зарядов, находящихся на расстоянии l. Ее электрическим моментом является вектор

где q – абсолютная величина каждого заряда,