 |
проводники с постоянными токами
|
|
|
|
При отсутствии токов в диэлектрике rotE = 0, т.е. E = – gradj; D = eE; divD = 0.
В случае однородной среды, когда e = const, эти уравнения дают divE = 0 или div grad j = 0, т.е. потенциал удовлетворяет уравнению Лапласа.
 Таким образом, в самом диэлектрике такое поле ничем не отличается от электростатического. Однако граничные условия на поверхности проводников уже не соответствуют тем, которые имеют место в электростатике. В случае электростатической задачи поверхность каждого проводника является поверхностью равного потенциала. При прохождении по проводнику электрического тока в проводнике возникает падение потенциала, и, следовательно, поверхность проводника уже не будет равнопотенциальной. Линии напряженности электрического поля в диэлектрике подходят к поверхности проводника не под прямым углом, так как на поверхности проводника появляется касательная составляющая напряженности поля в направлении линии тока. На рис. 3.1 показан характер линий напряженности электрического поля около проводов линии передачи. С принципиальной точки зрения, указанное обстоятельство существенно осложняет расчет поля, однако практически во многих случаях его можно не учитывать, так как обычно падение напряжения вдоль проводников на длине, сравнимой с расстоянием между проводниками, ничтожно мало по сравнению с разностью потенциалов проводников. Поэтому при рассмотрении электрического поля в диэлектрике, окружающем проводники с постоянными токами, можно использовать решения, полученные при рассмотрении соответствующих электростатических задач.
Таким образом, в самом диэлектрике такое поле ничем не отличается от электростатического. Однако граничные условия на поверхности проводников уже не соответствуют тем, которые имеют место в электростатике. В случае электростатической задачи поверхность каждого проводника является поверхностью равного потенциала. При прохождении по проводнику электрического тока в проводнике возникает падение потенциала, и, следовательно, поверхность проводника уже не будет равнопотенциальной. Линии напряженности электрического поля в диэлектрике подходят к поверхности проводника не под прямым углом, так как на поверхности проводника появляется касательная составляющая напряженности поля в направлении линии тока. На рис. 3.1 показан характер линий напряженности электрического поля около проводов линии передачи. С принципиальной точки зрения, указанное обстоятельство существенно осложняет расчет поля, однако практически во многих случаях его можно не учитывать, так как обычно падение напряжения вдоль проводников на длине, сравнимой с расстоянием между проводниками, ничтожно мало по сравнению с разностью потенциалов проводников. Поэтому при рассмотрении электрического поля в диэлектрике, окружающем проводники с постоянными токами, можно использовать решения, полученные при рассмотрении соответствующих электростатических задач.
3.2.Электрическое поле постоянного тока в проводящей среде
Рассмотрим электрическое поле постоянного тока в неподвижных проводящих средах, или проводниках.
|
|
|
3.2.1. Уравнения и основные соотношения электрического поля постоянного тока
Рассмотрим электрическое поле постоянного тока в неподвижных проводящих средах, или проводниках.
Из полной системы уравнений Максвелла выберем только те уравнения, которые описывают электрическое поле постоянного тока в проводящей среде:
 (1)
(1)
Применим к обеим частям первого уравнения системы (1) операцию дивергенции, с учетом получим
 .
.
Тогда уравнения Максвелла для электрического поля постоянного тока примут вид
 (2)
(2)
где согласно (3.6)
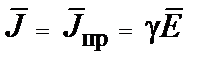 . (3)
. (3)
Одно из основных отличий электрического поля постоянного тока от электростатического обусловлено наличием внешних источников энергии неэлектростатического происхождения, без которых невозможно возникновение тока. В области действия этих источников, характеризуемых напряженностью  , (3) примет вид
, (3) примет вид
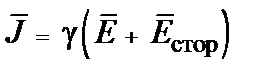 . (4)
. (4)
Выражение (3) представляет собой закон Ома в дифференциальной форме. Соотношение (4) является обобщенным законом Ома, или вторым законом Кирхгофа, в дифференциальной форме. Второе уравнение системы (2) называют первым законом Кирхгофа в дифференциальной форме.
Условие rotE = 0 свидетельствует, что вне источника ЭДС электрическое поле постоянных токов является так же, как и электростатическое поле, безвихревым. Такое поле является потенциальным, т.е. для характеристики может быть введена потенциальная функция φ, причем E = – grad j.
Из второго уравнения системы (2) следует, что линии вектора плотности тока непрерывны и замкнуты.
Два уравнения (2) можно объединить в одно, подобное уравнениям Пуассона-Лапласа.
Область, во всех точках которой  .
.
Для однородной проводящей среды ( ) из второго уравнения (2) с учетом (3) получим:
) из второго уравнения (2) с учетом (3) получим:
 . (5)
. (5)
Подставляя в (5) выражение 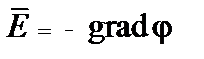 ,имеем:
,имеем:
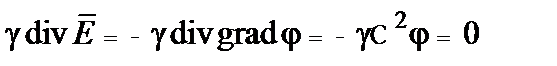 ,
,
т.е.
 . (6)
. (6)
Таким образом, электрическое поле в однородной проводящей среде в области вне источников энергии описывается уравнением Лапласа (6), как и электростатическое поле в однородной среде, где нет свободных зарядов.
|
|
|
3.2.2.Граничные условия на поверхности раздела
двух проводящих сред
На границе раздела сред функции 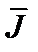 и
и  терпят разрыв. Уравнения для этих точек применять нельзя.
терпят разрыв. Уравнения для этих точек применять нельзя.
Получим граничные условия.
На границе раздела двух сред с различными проводимостями  и
и  выделим точку и окружим ее элементарной призмой, у которой высота бесконечно мала по сравнению с линейными размерами оснований (рис.3.2а).
выделим точку и окружим ее элементарной призмой, у которой высота бесконечно мала по сравнению с линейными размерами оснований (рис.3.2а).

Рис.3.2
Применяя первый закон Кирхгофа, получим:
 .
.
Откуда следует, что 
или  .
.
На границе раздела двух сред с различными проводимостями равны нормальные составляющие вектора плотности тока  .
.
Окружим точку элементарным прямоугольником (рис. 3.2б), у которого высота бесконечно мала по сравнению с длиной. Применяя второй закон Кирхгофа к контуру прямоугольника, получим:
 .
.
Откуда следует, что 
или  .
.
На границе раздела двух сред с различными проводимостями  и
и  равны тангенциальные составляющие вектора напряженности поля
равны тангенциальные составляющие вектора напряженности поля  .
.
Разделим почленно левые и правые части полученных уравнений и учтем, что  и
и  , в итоге получим:
, в итоге получим:
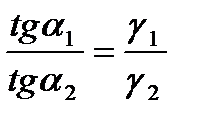 (7)
(7)
- условие преломления линий поля на границе раздела двух сред с различными проводимостями  и
и  .
.
3.2.3. Методы расчета электрических полей постоянного тока
Электрическое поле постоянного тока, с одной стороны, и электростатическое поле вне электрических зарядов (r =0), с другой стороны, описываются одинаковыми по структуре математическими уравнениями.
Аналогия электростатического поля и поля стационарных токов в проводящих средах обусловлена полной аналогией соответствующих уравнений для областей, лишенных сторонних источников (зарядов и токов соответственно. Привем эти уравнения в табл.1.
Таблица 1
| Электрическое поле постоянного тока | Электростатическое поле при отсутствии зарядов (r =0) |
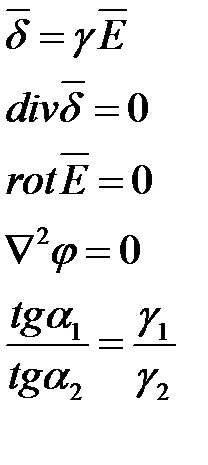
| 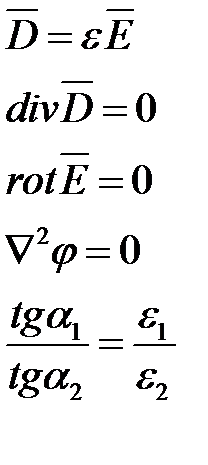
|
По своей природе электростатическое поле и электрическое поле постоянного тока в проводящей среде различны. Первое из них является полем неподвижных зарядов, второе – полем зарядов, движущихся с постоянной скоростью. Между величинами, характеризующими эти поля, существует математическая аналогия, т.е. они входят в уравнения одинаковым образом. Другими словами, уравнения полей и соотношения, записанные относительно математически аналогичных величин, выглядят одинаково.
|
|
|
Если два поля удовлетворяют одним и тем же уравнениям (уравнения Пуассона–Лапласа) и в них выполняются тождественные граничные условия для сходных (математически аналогичных) величин, то при одинаковой форме граничных поверхностей на основе теоремы единственности решения можно сделать вывод о том, что совокупности силовых и эквипотенциальных линий в этих полях (картины полей) будут одинаковыми.
Электростатическое поле в области, где нет свободных зарядов, описывается уравнением Лапласа так же, как и электрическое поле постоянного тока в области, где нет сторонних сил. Граничные условия для двух полей подобны. Величины 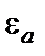 и
и  являются математически аналогичными. Можно сделать вывод об аналогии между зарядом
являются математически аналогичными. Можно сделать вывод об аналогии между зарядом  и током
и током  . Существует аналогия и между емкостью
. Существует аналогия и между емкостью 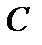 и проводимостью
и проводимостью 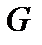 . Действительно, емкость между двумя телами, находящимися в среде с относительной диэлектрической проницаемостью
. Действительно, емкость между двумя телами, находящимися в среде с относительной диэлектрической проницаемостью 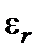 , равна
, равна
 . (8)
. (8)
Проводимость между этими телами, помещенными в проводящую среду с удельной проводимостью  можно записать как:
можно записать как:
 . (9)
. (9)
Поделив (8) на (9), получим:
 . (10)
. (10)
Математически аналогичные величины, характеризующие электростатическое поле и электрическое поле постоянного тока, сведены в табл. 2.
Т а б л и ц а 2
Электростатическое поле
( ) )
| Электрическое поле
в проводящей среде ( ) )
| |

| 
| 
|

| 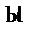
| 
|

| 
| 
|

| 
| 
|

| 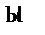
| 
|

| 
| 
|
Отмеченная аналогия лежит в основе расчета полей так называемым методом электростатической аналогии. Этот метод позволяет в ряде случаев при расчете токов в проводящей среде воспользоваться готовыми аналитическими решениями соответствующих задач электростатики, и наоборот, заменить исследование электростатического поля экспериментальным исследованием поля постоянного тока в проводящей среде. Последнее особенно важно при решении сложных задач электростатики, не имеющих аналитического решения. Так, согласно (10) можно рассчитать емкость по формуле
|
|
|
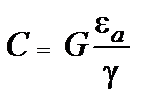 . (11)
. (11)
Тогда, экспериментально измерив проводимость 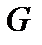 между телами (электродами), помещенными в проводящую среду, а также удельную проводимость среды
между телами (электродами), помещенными в проводящую среду, а также удельную проводимость среды  , по выражению (11) легко определить емкость между этими телами в среде с абсолютной диэлектрической проницаемостью
, по выражению (11) легко определить емкость между этими телами в среде с абсолютной диэлектрической проницаемостью  , поскольку геометрия полей в обеих задачах одинакова. Рассмотрим несколько примеров использования метода электростатической аналогии.
, поскольку геометрия полей в обеих задачах одинакова. Рассмотрим несколько примеров использования метода электростатической аналогии.
Метод электростатической аналогии.
Если в задаче с проводящими средами граничные поверхности имеют ту же форму и аналогичные граничные условия, что и в некоторой электростатической задаче, то можно использовать решение электростатической задачи, произведя в ней замену e на γ, D на δ, C на G.
Аналогичным же образом используется метод зеркальных изображений, в котором коэффициенты неполного отражения вычисляются по формулам: k 1 = 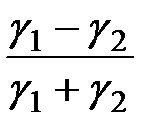 , k 2 =
, k 2 =  .
.
В прикладных задачах по расчёту полей в проводящих средах чаще всего требуется определить токи утечки и тепловые потери в изоляции кабелей и конденсаторов, а также параметры растекания тока заземлителей.
3.4.Задачи
Задача 1
При заданном векторе плотности тока
δ = 4 x × 1 x + 3 y × 1 y - 7 z × 1 z, (А/мм2)
определить значение потенциала φ (В) вида φ= Ax 2 + By 2 + Cz 2 в точке с
координатами x =3 (м), y =2 (м), z =1 (м) при известной удельной проводимости среды γ =10·106 (1/Ом·м).
Решение. Переведем заданный вектор плотности тока δ в (А/м2) и
по закону Ома в дифференциальной форме запишем вектор напряженности:
δ = 0,4 x 1 x+ 0,3 y 1 y+ 0,7 z 1 z,).
Далее на основании уравнения
E=- gradφ →…
В результате зависимость для потенциала будет следующей
j= Ax 2 + By 2 + Cz 2 = -0,2 x 2 - 0,15 y 2 + 0,35 z 2, (В)
тогда искомое значение потенциала в точке с координатами x =3 (м), y =2 (м), z =1 (м) составит:
j = -0,2 × (3)2 - 0,15× (2)2 + 0,35× (1)2 = -2,05 (В).
Задача 2.
Расчет тока утечки между двумя жилами коаксиального кабеля
Рассчитать ток утечки между двумя жилами коаксиального кабеля. Изоляция выполнена двухслойной из несовершенного диэлектрика (удельные проводимости g 1 = 5·10-8 См / м и g 2 = 2·10 -8 См / м, относительные диэлектриче-ские проницаемости er 1 = 2 и er 2 = 5). Напряжение U = 10 кВ. Геометрические размеры – r 1 = 1 мм, r 2 = 2 мм, r 3 = 3 мм.
Найти удельные тепловые потери в окрестности точки М, проводимости и ёмкости между телами, построить схему замещения системы. Кабель считать весьма протяжённым, а расчеты выполнить на единицу длины.
 Дополнительно определить предельно возможную длину кабеля как линии электропередачи.
Дополнительно определить предельно возможную длину кабеля как линии электропередачи.
|
|
|
Воспользуемся аналогией между электрическим полем в проводящей среде и электростатическим. ёмкости слоёв данного кабеля:
C10 =  =
=  = 160,4 пФ/м;
= 160,4 пФ/м;
C20 = 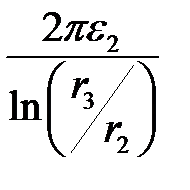 =
= 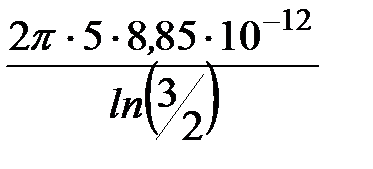 = 873,5 пФ/м.
= 873,5 пФ/м.
Проводимости слоёв и всего кабеля на единицу длины:
g 10 =  =
=  = 0,454·10-6 Cм / м;
= 0,454·10-6 Cм / м;
g 20 =  =
=  = 0,310·10-6 Cм / м;
= 0,310·10-6 Cм / м;
g 0 =  =
=  = 0,1842 мкСм / м.
= 0,1842 мкСм / м.
| U 2 |
| U 1 |
| g 02 |
| C 01 |
| I 0 |
| U |
| g 01 |
| C 02 |
Плотность тока в окрестности точки М:
d = i 0/ ( 2 pr 2 ) = 1,841·10-3/ ( 2 p ·2·10-3 ) = 0,147 А / м 2;
Удельные тепловые потери в окрестности точки М в слоях изоляции по закону Джоуля-Ленца:
p1 = d 2/g1 = 0,1472/(5·10-8) = 0,432·106 Вт/м3 = 0,432 МВт/м3;
p2 = d 2/g2 = 0,1472/(2·10-8) = 1,08·106 Вт/м3 = 1,08 МВт/м3.
Задача 3. Заземлитель в виде шара
Заземлитель в виде шара расположен на сравнительно небольшой глубине h, соизмеримой с его радиусом R.
Применим к решению задачи метод зеркальных отображений. Заменим в верхней полуплоскости диэлектрик  проводящей средой γ и зеркально расположим там такой же заземлитель, при этом граничные условия на поверхности земли не изменятся (линии вектора Е направлены по касательной вдоль поверхности). Заменим токи, стекающие с поверхностей обоих заземлителей, равными по величине точечными токами, растекающимися из электрических центров 1 и 2, которые будут смещены относительно геометрических центров так, чтобы сохранились прежними граничные условия на поверхности шаров (поверхности должны остаться эквипотенциальными с потенциалом φ=U).
проводящей средой γ и зеркально расположим там такой же заземлитель, при этом граничные условия на поверхности земли не изменятся (линии вектора Е направлены по касательной вдоль поверхности). Заменим токи, стекающие с поверхностей обоих заземлителей, равными по величине точечными токами, растекающимися из электрических центров 1 и 2, которые будут смещены относительно геометрических центров так, чтобы сохранились прежними граничные условия на поверхности шаров (поверхности должны остаться эквипотенциальными с потенциалом φ=U).

После определения положения электрических центров расчет параметров поля в произвольной точке n производится по методу наложения:

 .
.
При соотношении h>>R потенциал на поверхности заземлителя будет равен:
 , откуда следует формула для определения сопротивления заземлителя:
, откуда следует формула для определения сопротивления заземлителя:
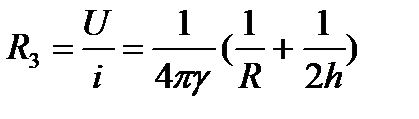 .
.
Задача 4.
Определить шаговое напряжение  на заданном расстоянии х от центра опоры высоковольтной ЛЭП при коротком замыкании одной из фаз линии на опору.
на заданном расстоянии х от центра опоры высоковольтной ЛЭП при коротком замыкании одной из фаз линии на опору.

Для упрощения расчетов будем считать, что заземлитель опоры имеет форму полушара с радиусом R. Заменим диэлектрик в верхней части пространства проводящей средой γ, а заземлитель дополним зеркальным отображением до полного шара. После таких преобразований решение задачи сводится к расчету поля шарового заземлителя:
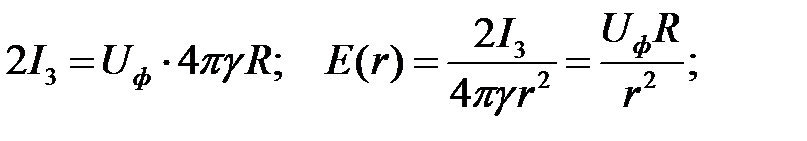
 .
.
где 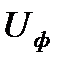 - фазное напряжение ЛЭП, R – радиус заземлителя (фундамента) опоры.
- фазное напряжение ЛЭП, R – радиус заземлителя (фундамента) опоры.
Вопросы для самопроверки
1. Электрический ток является векторной или скалярной величиной?
2. Как определить емкость двухпроводной линии путем моделирования ее полем постоянных токов?
3. Что такое "шаговое" напряжение, как его рассчитать?
4. Магнитное поле постоянных токов
Возникновение магнитного поля связано с движением электрических зарядов. Движение зарядов с постоянной скоростью порождает стационарное магнитное поле, не зависящее от времени и не связанное с электрическим полем.
4.1. Уравнения магнитного поля в интегральной и дифференциальной формах
Запишем уравнениями Максвелла для магнитного поля постоянного тока, или магнитостатики.
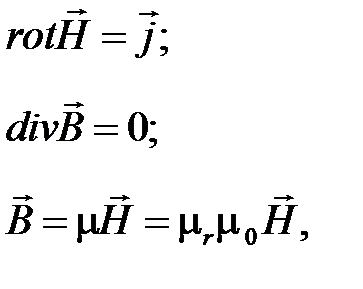 (4.1)
(4.1)
где m 0 = 4×p×10-7 » 1,257× 10-6 [Гн/м] - магнитная проницаемость пустоты; mr - относительная магнитная проницаемость.
Из первого уравнения (4.1) следует, что магнитное поле является вихревым (непотенциальным). Согласно второму уравнению (4.1) магнитное поле не имеет источников, линии вектора магнитной индукции непрерывны и замкнупиы.
В интегральной форме система (4.1) может быть представлена следующим образом:
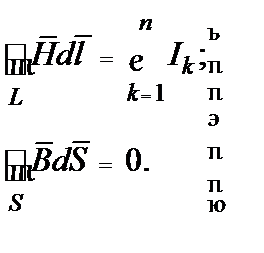 (4.2)
(4.2)
Первое уравнение (4.2) также называют законом полного тока. При вычислении алгебраической суммы в правой части уравнения положительными считаются токи, направления которых образуют правовинтовую систему с направлением обхода контура  . Второе уравнение (4.2) известно как принцип непрерывности линий магнитной индукции.
. Второе уравнение (4.2) известно как принцип непрерывности линий магнитной индукции.
Магнитное поле несет в себе энергию, плотность которой определятся уравнением:
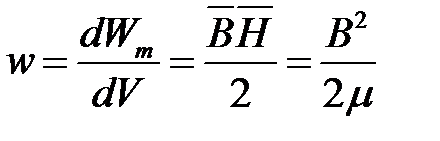 [ Дж/м3].
[ Дж/м3].
Вектор индукции магнитного поля можно записать в виде
 , (4.3)
, (4.3)
где  – вектор намагниченности, или магнитный момент единицы объема.
– вектор намагниченности, или магнитный момент единицы объема.
Вектор  характеризует намагниченность вещества в магнитном поле подобно тому, как вектор поляризации
характеризует намагниченность вещества в магнитном поле подобно тому, как вектор поляризации  характеризует поляризацию вещества в электрическом поле.
характеризует поляризацию вещества в электрическом поле.
Способность намагничиваться в магнитном поле характеризуется относительной магнитной проницаемостью  . У диамагнитных веществ относительная магнитная проницаемость немного меньше единицы (
. У диамагнитных веществ относительная магнитная проницаемость немного меньше единицы (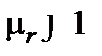 ), у парамагнитных веществ – немного больше единицы (
), у парамагнитных веществ – немного больше единицы ( ). Магнитная проницаемость ферромагнитных веществ значительно превышает единицу (
). Магнитная проницаемость ферромагнитных веществ значительно превышает единицу (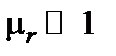 ), к таким веществам относят железо, никель, кобальт и их сплавы, ферриты и др., их магнитная проницаемость достигает
), к таким веществам относят железо, никель, кобальт и их сплавы, ферриты и др., их магнитная проницаемость достигает  . На практике все вещества делят на ферромагнитные (
. На практике все вещества делят на ферромагнитные ( ) и неферромагнитные (
) и неферромагнитные (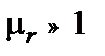 ).
).
Вектор намагниченности  пропорционален напряженности магнитного поля
пропорционален напряженности магнитного поля  :
:
 . (4.4)
. (4.4)
Важной характеристикой магнитного поля является магнитный поток  сквозь любую поверхность
сквозь любую поверхность  ], равный
], равный
 . (4.5)
. (4.5)
Напомним размерности обсуждаемых величин в системе СИ:
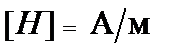 ,
,  ,
,  .
.
Между векторами 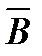 и
и 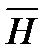 существует связь:
существует связь:
 ,
,
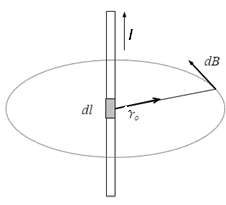 Известный из курса физики закон Био-Савара-Лапласа устанавливает связь между элементарным вектором магнитной индукции
Известный из курса физики закон Био-Савара-Лапласа устанавливает связь между элементарным вектором магнитной индукции  в произвольной точке пространства и элементом тока
в произвольной точке пространства и элементом тока  :
:


На основе закона Био-Савара-Лапласа выполняется расчет магнитного поля сложных систем проводников с токами.
Закон Ампера определяет силу взаимодействия магнитного поля на элеент проводника с током:
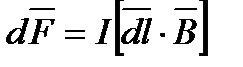 ,
,
откуда следует, что сила, действующая на проводник, равна
 .
.
На прямолинейный проводник с током I в равномерном магнитном поле действует сила  , направление которой определяется по правилу левой руки.
, направление которой определяется по правилу левой руки.
4. 2. Векторный потенциал магнитного поля
Как ясно из первого уравнения (4.1), ввести для описания свойств магнитного поля некоторую скалярную функцию  подобно тому, как вводится потенциальная функция
подобно тому, как вводится потенциальная функция  (см. раздел 4.3), невозможно, так как
(см. раздел 4.3), невозможно, так как 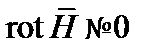 . Однако из второго уравнения (4.1) следует, что можно ввести некоторую векторную функцию
. Однако из второго уравнения (4.1) следует, что можно ввести некоторую векторную функцию  , которая связана с вектором магнитной индукции соотношением:
, которая связана с вектором магнитной индукции соотношением:
 . (4.6)
. (4.6)
Выражение (4.6) вытекает из второго уравнения (4.1) автоматически, поскольку всегда
 .
.
Векторную функцию  называют векторным потенциалом, или векторной потенциальной функцией, магнитного поля.
называют векторным потенциалом, или векторной потенциальной функцией, магнитного поля.
Вектор  связан с векторной потенциальной функцией
связан с векторной потенциальной функцией  с точностью до
с точностью до 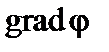 :
:
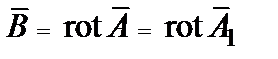 , (4.7)
, (4.7)
где  .
.
Фактически, это означает, что если к векторному полю (магнитному) прибавить любое поле потенциальное (электрическое), сам векторный потенциал  изменится, а магнитное поле
изменится, а магнитное поле  – нет. В самом деле
– нет. В самом деле
 .
.
Таким образом, векторный потенциал  может быть выбран произвольным образом, лишь бы соблюдалось условие (4.6). Это очень удобно, поскольку при расчетах магнитного поля вектору
может быть выбран произвольным образом, лишь бы соблюдалось условие (4.6). Это очень удобно, поскольку при расчетах магнитного поля вектору  можно присвоить такие свойства, что решение задачи станет значительно проще.
можно присвоить такие свойства, что решение задачи станет значительно проще.
Для векторной функции  можно получить уравнения, подобные уравнениям Пуассона-Лапласа. Именно поэтому ее и назвали векторным потенциалом.
можно получить уравнения, подобные уравнениям Пуассона-Лапласа. Именно поэтому ее и назвали векторным потенциалом.
Получимуравнение для векторного потенциала. Рассмотрим случай однородной изотропной среды ( ), когда вектора
), когда вектора  и
и  связаны соотношением (3.4). Умножая первое уравнение (7.1) на
связаны соотношением (3.4). Умножая первое уравнение (7.1) на  , с учетом (3.4) получим:
, с учетом (3.4) получим:
 . (4.8)
. (4.8)
Подставляя (7.6) в (7.8), имеем:
 . (4.9)
. (4.9)
В соответствии с правилами векторной алгебры левая часть (4.9) может быть преобразована следующим образом:
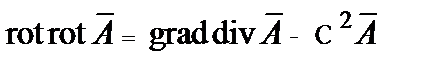 ,
,
тогда уравнение (7.9) примет вид:
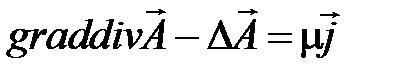 . (4.10)
. (4.10)
Возьмем такой вектор  , чтобы уравнение (4.10) стало как можно более простым, например, пусть
, чтобы уравнение (4.10) стало как можно более простым, например, пусть
 .
.
В этом случае уравнение (4.10), а значит, и систему (4.1) можно представить как
 . (4.11)
. (4.11)
Одному векторному уравнению (7.11) соответствуют три скалярных относительно проекций вектора  в выбранной системе координат. В декартовой системе получим:
в выбранной системе координат. В декартовой системе получим:
 (4.12)
(4.12)
Уравнение (7.11) и соответствующая ему система (7.12) определяют вектор  в области, где протекают токи (
в области, где протекают токи ( ). В областях, свободных от токов, т.е. при
). В областях, свободных от токов, т.е. при  , указанные уравнения примут вид:
, указанные уравнения примут вид:
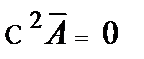 .
.
Выражения (4.12) по форме записи совпадают с уравнением Пуассона для скалярной потенциальной функции 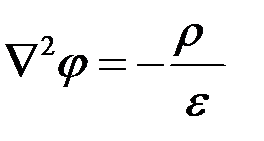 . Между уравнениями существует математическая аналогия. Следовательно, решение (4.12) совпадает с решением уравнения Пуассона для электростатического поля при аналогичных граничных условиях.
. Между уравнениями существует математическая аналогия. Следовательно, решение (4.12) совпадает с решением уравнения Пуассона для электростатического поля при аналогичных граничных условиях.
Решение уравнения Пуассона известно и имеет вид
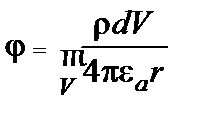
Используя математическую аналогию между величин ( ,
,  ), запишем решение уравнений (4.12):
), запишем решение уравнений (4.12):
 , (4.13)
, (4.13)
где  ,
,  ,
, 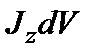 – проекции элемента тока
– проекции элемента тока  ,
,  – расстояние от элемента тока до точки, в которой определяется магнитное поле. Умножая соотношения (4.13) на соответствующие единичные вектора и складывая их почленно, получим решение:
– расстояние от элемента тока до точки, в которой определяется магнитное поле. Умножая соотношения (4.13) на соответствующие единичные вектора и складывая их почленно, получим решение:
 . (4.14)
. (4.14)
Решение уравнений (4.11), (4.12) в виде (4.13), (4.14) получается и используется при условии существования токов в ограниченном объеме пространства, что на практике всегда имеет место. При этом, как ясно из (4.13) и (4.14), величина векторного потенциала убывает по мере удаления от области, занятой токами, в бесконечность не медленнее, чем  . Так как магнитная индукция
. Так как магнитная индукция  определяется зависимостью
определяется зависимостью  , а операция
, а операция  – есть векторно-пространственная производная, то
– есть векторно-пространственная производная, то  и соответственно напряженность магнитного поля
и соответственно напряженность магнитного поля  убывают в бесконечность не медленнее, чем
убывают в бесконечность не медленнее, чем  .
.
 Рассмотрим теперь пути нахождения магнитного поля в наиболее важном случае линейного тока. Пусть известна плотность
Рассмотрим теперь пути нахождения магнитного поля в наиболее важном случае линейного тока. Пусть известна плотность
линейного тока J. Тогда
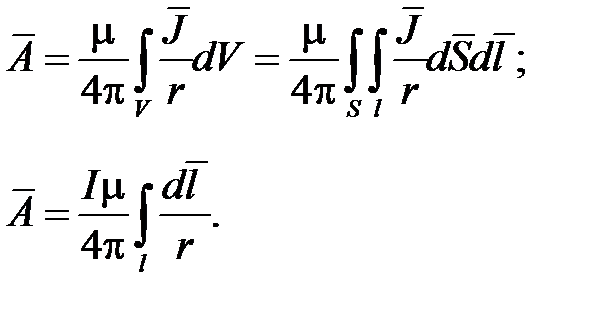
Так как ток 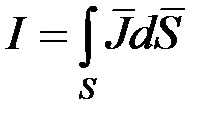 , то
, то
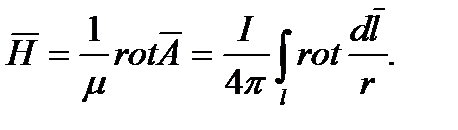 (4.15)
(4.15)
Определим подынтегральное выражение.
Пусть  , тогда
, тогда
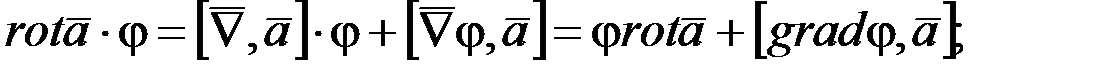
Соответственно
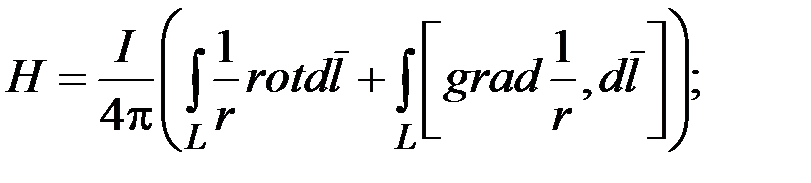
Так как dl не зависит от положения точки М, в которой находим ротор, то  а
а 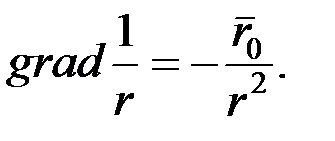
Подставив полученные результаты в уравнение (4.15) получаем

Это интегральная формулировка закона Био и Савара, непосредственно связывающего напряженность магнитного поля с линейным распределением тока.
В дифференциальной форме этот закон имеет вид:

4.3. Выражение магнитного потока
|
|
|


