II. Расчет зубчатых колес редуктора.

ВВЕДЕНИЕ

Редуктором называют механизм, состоящий из зубчатых или червячных передач, выполненный в виде отдельного агрегата и служащий для передачи вращения от вала двигателя к валу рабочей машины. Кинематическая схема привода может включать, помимо редуктора, открытые зубчатые передачи, цепные или ременные передачи. Указанные механизмы являются наиболее распространенной тематикой курсового проектирования.

Назначение редуктора — понижение угловой скорости и соответственно повышение вращающего момента ведомого вала по сравнению с ведущим. Механизмы для повышения угловой скорости, выполненные в виде отдельных агрегатов, называют ускорителями или мультипликаторами.

Редуктор состоит из корпуса (литого чугунного или сварного стального), в котором помещают элементы передачи — зубчатые колеса, валы, подшипники и т. д. В отдельных случаях в корпусе редуктора размещают также устройства для смазывания зацеплений и подшипников (например, внутри корпуса редуктора может быть помещен шестеренный масляный насос) или устройства для охлаждения (например, змеевик с охлаждающей водой в корпусе червячного редуктора).

Редуктор проектируют либо для привода определенной машины, либо по заданной нагрузке (моменту на выходном валу) и передаточному числу без указания конкретного назначения. Редукторы классифицируют по следующим основным признакам: типу передачи (зубчатые, червячные или зубчато-червячные); числу ступеней (одноступенчатые, двухступенчатые и т. д.); типу зубчатых колес (цилиндрические, конические, коническо-цилиндрические и т. д.); относительному расположению валов редуктора в пространстве (горизонтальные, вертикальные); особенностям кинематической схемы (развернутая, соосная, с раздвоенной ступенью и т. д.).

В настоящем задании мы рассмотрим проектирование горизонтального конического редуктора с техническими характеристиками и параметрами работы:

 

1. Мощность на тихоходном валу- Рт кВт = Рт=7кВт.

2. Угловая скорость тихоходного вала Wт=62рад/с.

3. Коэффициент перегрузки- 2,2.

4. Число смен работы за сутки- 2 .

5. Срок службы привода в годах- 5лет.

I. Выбор электродвигателя и кинематический расчет

 

Наибольшее распространение в промышленности получили трёхфазные асинхронные двигатели с короткозамкнутым ротором. Эти двигатели просты в конструкции и обслуживании, надёжны в эксплуатации, имеют небольшую стоимость.

Расчёт привода начинают с определения общего КПД кинематической схемы, общего передаточного числа и выбора электродвигателя.

По таблице 1.1 (1,стр.5)примем:

КПД пары конических зубчатых колес ŋ₁ =0,97;

Коэффициент, учитывающий потери на трение, в паре подшипников качения вала ŋ₂=0.99.

Общий КПД привода: ŋ = ŋ ₁·ŋ₂ = 0,97·0,99= 0,95

Требуемая мощность электродвигателя:

Частота вращения тихоходного вала:

 

По таблице П1(1)приложения (ГОСТ 19523-81),(1,стр.390) по требуемой мощности выбираем электродвигатель 4А132S4Y3,

асинхронный, серии 4А, закрытый, обдуваемый, с синхронной частотой вращения n с, с мощностью , и скольжением S%.

 

Рдв кВт	Типоразмер	nc об/мин	s %	nн, об/мин	Wн	U	Up
7,5	112М2		2,5		306,25	4,94	х
7,5	132S4				152,34	2,46	2,5
7.5	132M6		3,2		101,35	1,63	х
7.5	160S8		2,5	731.25	76,56	1,23	х

 

Номинальные частоты вращения:

n_н = n_с∙ (1-S/100)

nн1=3000∙(1-2,5/100)=2925(^об/_мин)

n_н2=1500∙(1-3/100)=1455(^об/мин)

n_н3=1000∙(1-3,2/100)=968(^об/мин)

n_н4=750∙(1-2,5/100)=731.25(^об/мин)

Номинальная угловая скорость двигателя:

wн n_н∙0,1047

wн1 = n_н1∙0,1047=306,2(с^-1)

wн2 = n_н2∙0,1047=152,3(с^-1)

wн3 = n_н3∙0,1047=101,3(с^-1)

wн4 = n_н4∙0,1047=76,6(с^-1)

U = =

Двигатели 112М2, 132М6 и 160S8 не подходят, так как передаточное число не входит в допустимый промежуток для конической передачи:

Для двигателя 132S4

U_p2 = 2,5 U₂ = 2,46­

U₂ / U_p2 ∙ 100% = 2,46/2,5∙ 100% =98,4%

1,6% - относительная погрешность.

Для двигателя 132S4 погрешность единственно-допустимая, следовательно выбираем этот двигатель (ГОСТ 2185-66).

Частоты вращения и угловые скорости валов редуктора:

ведущего вала

n₁ = n_н =1455 (^об/_мин)

w₁ = w_н =152,34 (^рад/_с)

ведомого вала

n₂ = n₁ / U_p= 582 (^об/_мин)

w₂ = w₁/ U_p =60,94 (^рад/_с)

 

 

Вращающие моменты на валах редуктора:

на валу шестерни:

T₁ = = = 49,23 (Н ·м)

на валу колеса

T₂ = T₁· U_p · η = 116,92(Н ·м)

 

Вал	Рдв, (кВт)	n, (об/мин)	W, с-1	Т, (Н ·м)
	7,37		152,34	49,23
			60,94	116,92

 

II. Расчет зубчатых колес редуктора.

 

Примем для шестерни и колеса одну и ту же марку стали с различной термообработкой.

По таблице 3.3 принимаем материалы со средними механическими характеристиками, для шестерни сталь 40Х улучшенную с твердостью НВ 270; для колеса - сталь 40X улучшенную с твердостью НВ 245.

2.1. Проектировочный расчёт

По табл.3.2 принимаем для шестерни и колеса пределы контактной выносливости:

σ_Hlimb = 2·HB +70=2·245+70=560МПа;

Срок службы привода в часах

.

Число циклов нагружений зубьев колеса

;

Базовое число циклов для материала колеса(по табл.3.2(1))

;

Коэффициент долговечности

;

Следовательно, при длительной эксплуатации коэффициент долговечности . Примем коэффициент безопасности [S_H] = 1,15, тогда

Допускаемые контактные напряжения (по формуле (3.9)):

[σ_H] = где σ_Hlimb — предел контактной выносливости при базовом числе циклов.

Коэффициент K_HB при консольном расположении шестерни примем равным K_Hβ=1,35 (1,табл. 3.1, стр. 32).Коэффициент ширины венца по отношению к внешнему конусному расстоянию ψ_bRe=0,285 (рекомендация ГОСТ 12289-76(1)).

Внешний делительный диаметр колеса (по формуле (3.29), стр. 49)

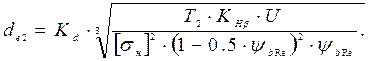
В этой формуле для прямозубой передачи K_d=99; передаточное число

U =2,5;

.

Принимаем по ГОСТ 12289-76 ближайшее стандартное значение d_e2=200 мм (1,стр. 49).

Отклонение от заданного , погрешность меньше предельно допустимой 2%.

 

 

Число зубьев шестерни из интервала 18-32 примем z₁=25.

Число зубьев колеса

z₂=z₁∙ U =25∙2,5=62,5

Тогда примем z₂=63.

Отклонение от заданного , погрешность меньше предельно установленных ГОСТ 12289-76, допустимых 3%.

Внешний окружной модуль(1,стр.50)

Примем m_e = 3,2 уточняем значение d_e2=m_ez₂=201,6 мм.

Отклонение от стандартного значения , что менее допустимых 2%.

Углы делительных конусов

Внешнее конусное расстояние R_e и длина зуба b:

Принимаем b=31мм.

 

Внешний делительный диаметр шестерни

d_e1=m_e·z₁=3,2·25=80мм.

Средний делительный диаметр шестерни

d₁=2(R_e-0,5b)sinδ₁ = 2∙(108.45-0,5∙31)sin21 39' = 68,59мм;

 

Внешние диаметры шестерни и колеса(по вершинам зубьев):

d_ae1=d_e1+2m_e cosδ₁=80+2·3.2cos21 39';

d_ae1=85,9 мм;

d_ae2=d_e2+2m_e cosδ₂=201,6+2·3.2cos68 21';

d_ae2=203мм.

Средний окружной модуль

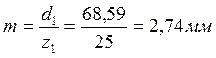
Коэффициент ширины шестерни по среднему диаметру

.

Средняя окружная скорость колёс

Для конических передач обычно назначают 7-ю степень точности.

 

2.2. Проверочный расчёт на контактную выносливость

Для проверки контактных напряжений определяем коэффициент нагрузки:

K_H=K_Hβ K_HαK_Hυ =1.2∙1∙1.05=1,26.

По таблице 3.5 (стр. 39) при Ψ_bd=0,451 консольном расположении колёс и твёрдости HB<350 коэффициент, учитывающий распределение нагрузки по длине зуба, K_Hβ=1,2.

Коэффициент, учитывающий распределение нагрузки между прямыми зубьями, K_Hα=1,0 (таблица 3.4).

 

Коэффициент, учитывающий динамическую нагрузку в зацеплении, для прямозубых колёс при υ 5 м/с K_Hυ=1,05 (таблица 3.6).

Таким образом K_H=1.2∙1∙1,05=1,26.

Проверяем контактное напряжение по формуле 3.27 (стр. 47).

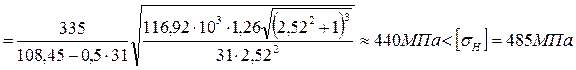
Силы зацепления

Силы в зацеплении:

окружная сила

;

радиальная для шестерни, равная окружной для колеса,

осевая для шестерни, равная радиальной для колеса,

 

2.4. Проверочный расчёт на выносливость зубьев

По напряжениям изгиба

Проверка зубьев на выносливость по напряжениям изгиба (ф.3.31, стр.50)

.

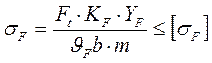Здесь =0,85 ­– опытный коэффициент, учитывающий понижение нагрузочной способности конической прямозубой передачи по сравнению с цилиндрической.

­– коэффициент нагрузки у .

K_Fβ=1,11 ­ – коэффициент, учитывающий распределение нагрузки по длине зуба, берётся из таблицы 3.7 при Ψ_bd=0,451 консольном расположении шестерни, валах на роликовых подшипников и твёрдости HB<350.

K_Fυ=1,45 –коэффициент, учитывающий распределение нагрузки в зацеплении для прямозубых колёс берётся по таблице 3.8 при твердости HB<350, скорости υ=5.0 м/с и седьмой степени точности.

Итак,

Y_F-коэффициент формы зуба выбираем в зависимости от эквивалентных чисел зубьев:

для шестерни ;

для колеса .

При этом Y_F2=3.6(1,стр. 42).

Допускаемое напряжение при проверке зубьев на выносливость по напряжениям изгиба:

Предел выносливости при изгибе по таблице 3.9 для стали 40Х улучшенной при твердости НВ < 350

Для шестерни: = 1,8·270 = 486 МПа;

Для колеса: = 1,8·245 = 441 МПа.

Коэффициент запаса прочности [S_F] = [S_F]'[S_F]''. По таблице 3.9

[S_F]’ = 1,75, учитывая нестабильность механических свойств для поковок и штамповок

[S_F]” = 1. [S_F] = 1.75·1=1.75.

 

Допускаемые напряжения при расчёте зубьев на выносливость:

для шестерни:

для колеса:

Находим отношение :

для шестерни:

для колеса:

Дальнейший расчет ведём для зубьев колеса, так как полученное отношение для него меньше.

Проверяем зуб шестерни:

Условие прочности выполненяется.

 

2.5. Проверочный расчет на контактную статическую прочность при пиковой нагрузке

Расчётные контактные напряжения при пиковой нагрузке по формуле

.

Допускаемое контактное напряжение под действием максимальной нагрузки для стальных колес с улучшением

,

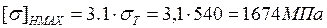где предел текучести для стали Ст 40Х при диаметре заготовки >160мм.

Условие прочности выполняется.

2.6. Проверочный расчёт на изгибную статическую

1234Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: