 |
Примеры использования метода секущих плоскостей
|
|
|
|
Оглавление
Введение........................................................................................................... 4
Оформление работы....................................................................................... 4
Методические указания по выполнению задач.......................................... 5
Задача №1......................................................................................................... 5
Примеры использования метода секущих плоскостей............................ 7
Задача №2....................................................................................................... 13
Примеры использования метода вспомогательных сфер.................... 14
Задача №3....................................................................................................... 18
Примеры построения разверток поверхностей....................................... 19
Список литературы........................................................................................ 22
Приложение 2. Варианты заданий к задачам №2 и №3........................ 37
Приложение 3. Образец оформления задачи №1.................................. 44
Приложение 4. Образец оформления задач №2 и №3.......................... 45
Введение
Целью данной работы является развитие навыков построения проекций поверхностей, линий их пересечения, а также разверток поверхностей.
Работа состоит из 3 задач.
Задача №1. Построить три проекции заданных поверхностей и проекции линий их взаимного пересечения, используя в качестве посредников вспомогательные секущие плоскости. Варианты заданий приведены в прил. 1.
Задача №2. Построить одну (фронтальную) проекцию заданных пересекающихся поверхностей и линию их взаимного пересечения, используя в качестве посредников вспомогательные сферические поверхности. Варианты заданий содержатся в прил. 2.
Задача №3.Построить приближенную развертку поверхности, помеченной в задании к задаче №2 буквой «P».
Оформление работы
|
|
|
Задания оформляются в виде двух эпюров, каждый из которых выполняется карандашом в масштабе 1:1 на отдельном листе чертежной бумаги формата А3:
· Эпюр 1401 содержит задачу №1.
· Эпюр 1411 включает в себя задачи №2 и №3.
Оформление эпюров должно быть выполнено в соответствии со стандартами ЕСКД:
· по ГОСТ 2.301 – 68 – форматы листов;
· по ГОСТ 2.303 – 68 – типы линий;
· по ГОСТ 2.304 – 81 – чертежный шрифт;
· по ГОСТ 2.307 – 68 – простановка размеров;
· по ГОСТ 2.104 – 68 – основная надпись, форма 1.
 Обозначение документов в основной надписи выполняется по типу:
Обозначение документов в основной надписи выполняется по типу:
Например, обозначение эпюров для 24-го варианта:
1401. 000 000. 024 – эпюр №1.
1411. 000 000. 024 – эпюр №2.
В прил. 3, 4 приведены образцы оформления эпюров.
Методические указания по выполнению задач
Задача №1
1. Вычертить фронтальную и горизонтальную проекции заданных поверхностей в соответствии с индивидуальным заданием.
2. Используя проекционные связи, построить профильную проекцию поверхностей.
3. Основываясь на полученных в курсе начертательной геометрии теоретических знаниях, определить характер линий пересечения поверхностей, а также вид каждой проекции линий пересечения, которые требуется построить. Например:
· линия пересечения поверхностей многогранников с поверхностями вращения – плоская кривая; она может состоять из дуг окружностей, эллипсов, парабол, гипербол. Проекцией плоской кривой может быть как отрезок прямой, так и плоская кривая;
· линия пересечения двух соосных поверхностей вращения – окружность;
· если в 2 пересекающиеся поверхности вращения можно вписать общую для них сферу, то линия пересечения распадается на 2 плоские кривые (теорема Монжа);
· в общем случае две поверхности вращения пересекаются по пространственным кривым, проекции которых – плоские кривые.
4. Выявить характерные точки, построить их недостающие проекции. К характерным точкам относятся:
|
|
|
· точки, расположенные на очерковых образующих поверхности вращения (в плоскости главного меридиана или в плоскости, перпендикулярной плоскости главного меридиана);
· точки, расположенные на экваторе;
· точки, расположенные на ребрах многогранника;
· точки, проекции которых отделяют видимую часть проекции линии пересечения от невидимой части;
· точки, определяющие большую и малую оси эллипсов;
· высшие и низшие точки линии пересечения относительно плоскости π1, ближайшие и наиболее удаленные по отношению к наблюдателю, крайние слева и крайние справа на проекциях линии пересечения.
5. Построить промежуточные точки, принадлежащие линии пересечения поверхностей.
Количество промежуточных точек определяется в зависимости от сложности формы проекции линии пересечения. Малое количество точек не позволяет выявить характер кривой. Слишком большое количество точек также не улучшает вид проекции, так как неизбежные погрешности в определении точек искажают форму кривой.
Например, если проекция линии пересечения – эллипс, то для ее построения требуется всего 8 точек (вместе с характерными точками).
Построение промежуточных точек осуществляется следующим образом:
· поочередно проводят несколько вспомогательных секущих плоскостей-посредников. Плоскости выбирают так, чтобы линии пересечения той и другой поверхности плоскостью были простейшими – окружностями или отрезками прямых линий;
· строят линии пересечения каждой плоскости-посредника с заданными поверхностями;
· находят точки пересечения построенных линий. Эти точки – общие для пересекающихся поверхностей, следовательно, они лежат на линии их пересечения.
6. Определить видимость точек. Видимые точки соединить последовательно сплошной основной линией с учетом характера кривой (для гладкой кривой, отличающейся от дуги окружности, используется лекало).
Таким же образом соединить невидимые точки, используя невидимую (тонкую штриховую) линию.
7. Выполнить обводку проекций поверхностей с учетом видимости.
Примеры использования метода секущих плоскостей
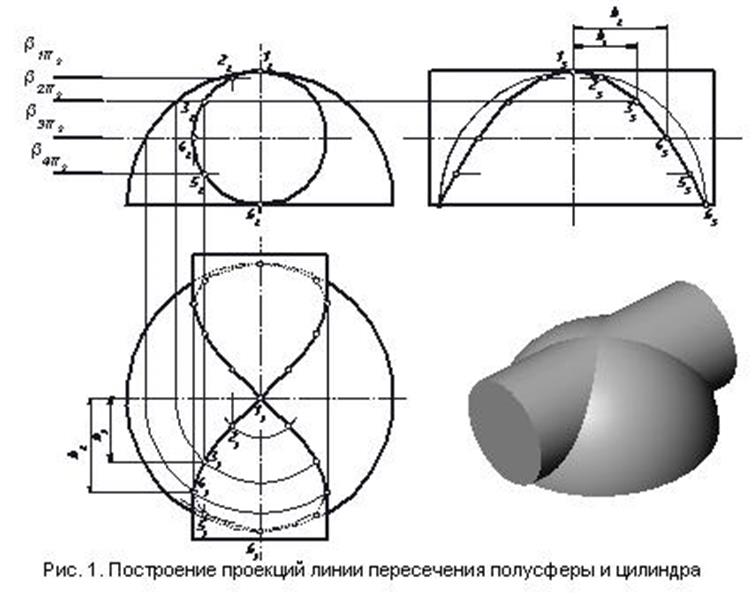
Пример 1. Построение проекций линии пересечения полусферы и цилиндра (рис. 1.)
|
|
|
Линия пересечения в данном случае является биквадратной кривой (кривой Вивиани).
Поскольку по отношению к фронтальной плоскости проекций поверхность цилиндра является проецирующей, то фронтальная проекция линии пересечения является окружностью и совпадет с очерком цилиндра.
Профильная проекция линии пересечения заданных полусферы и цилиндра будет представлять собой параболу с вершиной в точке 1, так как поверхности имеют общую плоскость симметрии, параллельную профильной плоскости проекций.
На горизонтальной плоскости проекций должна получиться плоская кривая, имеющая 2 оси симметрии.
Построение начнем с фронтальной плоскости проекций, так как фронтальная проекция поверхностей содержит проекцию линии их пересечения (окружность).
1. Выделим проекции характерных точек – 12, 42, 62. В качестве промежуточных точек выберем произвольные точки, примерно равномерно расположенные между характерными точками – 22, 32, 52 .
2. Определим горизонтальную и профильную проекции характерных точек 1 и 6, исходя из того, что точка 1 лежит на главном меридиане, а точка 6 – на экваторе полусферы.
3. Найдем недостающие проекции точки 4.
Для этого проведем через эту точку вспомогательную горизонтальную плоскость β 3 (след β3 π2). Плоскость β 3 пересечет полусферу по окружности, построение которой показано на рис.1, а цилиндр – по двум крайним образующим (они совпадают с очерком цилиндра на плоскости π1). Пересечение этих линий дает проекцию точки 41.
Профильную проекцию точки 4 определим, проведя линию проекционной связи от фронтальной проекции точки, с одной стороны, а с другой – измерим расстояние по оси У между плоскостью главного меридиана и точкой 41 (отрезок b2 на рис. 1) и отложим это расстояние по оси У на плоскости π3. В результате получим точку 43.
4.Для определения проекций оставшихся выделенных точек следует для каждой из них повторять действия, описанные в пункте 3.
5. Определим видимость точек. На горизонтальной плоскости проекций будут видимы только точки, фронтальные проекции которых расположены выше плоскости β 3 (границей видимости будет являться точка 4). На профильной плоскости проекций все точки левой половины линии пересечения будут видимы.
|
|
|
6. Соединим плавной линией полученные проекции точек с учетом их видимости в последовательности, определенной на фронтальной проекции.
Пример 2. Построение двух проекций линии пересечения цилиндра и конуса приведено на рис. 2.
Как и в первом примере, фронтальная проекция линии пересечения совпадает с очерком цилиндра. Поэтому построение начнем с выделения фронтальных проекций общих точек обеих поверхностей.
Характерными являются следующие точки:
· 1 и 2, – принадлежащие плоскости главного меридиана конуса;
· 3 и 7 – соответственно самая высокая и самая низкая точки;
· 4 и 6, – лежащие в плоскости, перпендикулярной плоскости главного меридиана конуса, следовательно, их фронтальные проекции будут располагаться на очерке конуса;
· 5 – самая правая точка.
Горизонтальные проекции точек 1 и 2 определяются проведением линий проекционной связи.
Остальные проекции точек строятся при помощи проведения через них вспомогательных горизонтальных плоскостей.
Видимость точек на горизонтальной плоскости проекций определяет плоскость β 3: все точки, фронтальные проекции которых лежат выше плоскости β 3, будут видимы, ниже – невидимы (граница видимости – точка 5).
Пример 3. Построение трех проекций линии пересечения цилиндра и конуса (рис. 3).
Так как в данном случае горизонтальная проекция линии пересечения совпадает с очерком цилиндра, вначале определяем горизонтальные проекции общих точек цилиндра и конуса. Выделим следующие характерные точки:
· 1, – принадлежащая экватору конуса;
· 5 – самая высокая точка;
· 3 и 3’, – лежащие в плоскости главного меридиана цилиндра, следовательно, их фронтальные проекции будут располагаться на очерке цилиндра.
Точки 2, 2’, 4, 4’ – промежуточные, взятые произвольно.
Проекции точки 1 определяем по проекционным связям. Остальные проекции находим следующим образом.
1. Через выделенные горизонтальные проекции точек последовательно проводим горизонтальные проекции параллелей конуса, определяем радиус каждой параллели. Затем находим фронтальную проекцию каждой параллели.
2. Поскольку каждая параллель конуса лежит в соответствующей горизонтальной плоскости, строим фронтальные следы этих плоскостей и принимаем их за вспомогательные секущие плоскости.
3. В каждой вспомогательной плоскости, проведя линии проекционной связи, находим фронтальные проекции выделенных точек.
|
|
|
4. Находим профильные проекции точек, для чего измеряем расстояние вдоль оси У (т.е. по вертикали) от горизонтальной проекции каждой точки до горизонтальной оси конуса (Y1, Y2, Y3, Y4). Затем на плоскости π3 это расстояние откладываем от вертикальной оси конуса вправо в соответствующей секущей плоскости.


Задача №2
1. Вычертить заданную фронтальную проекцию поверхностей.
2. Определить характер кривой линии пересечения поверхностей. Так как обе заданные поверхности – поверхности вращения, то линия их пересечения есть биквадратная пространственная кривая. В данном задании обе поверхности вращения имеют общую плоскость симметрии, параллельную фронтальной плоскости проекций. Поэтому фронтальная проекция линии их пересечения является кривой 2-го порядка.
3. Определить характерные точки, принадлежащие линии пересечения поверхностей. Вследствие условий, указанных в пункте 2, характерные точки будут совпадать с точками пересечения очерков поверхностей.
4. Построить промежуточные точки линии пересечения методом концентрических сфер-посредников. Алгоритм построения следующий:
· задаем центр сфер-посредников. Как правило, это точка пересечения осей вращения поверхностей;
определяем пределы изменения радиуса сферы-посредника: Rmin < R < Rmax.
Rmax равен расстоянию от заданного центра сфер до наиболее удаленной характерной точки. Rmin равен радиусу сферы, вписанной в большую поверхность и пересекающей меньшую поверхность;
· строим сферу минимального радиуса. Линия её пересечения с каждой из заданных поверхностей есть окружность (в данном случае сфера касается большей поверхности и пересекает меньшую поверхность по окружности). В пересечении окружностей находим точки, общие для заданных поверхностей, а следовательно, принадлежащие линии пересечения этих поверхностей.
Каждая из окружностей лежит в плоскости, перпендикулярной оси вращения соответствующей поверхности. В силу того, что оси вращения обеих поверхностей параллельны плоскости π2, окружности проецируются на π2 в виде прямолинейных отрезков, что облегчает построение точек пересечения окружностей;
· проводим еще 2 – 3 сферы, радиус которых лежит в определенном выше диапазоне. При построении каждой сферы находим линии ее пересечения с заданными поверхностями, а затем точки пересечения линий;
· если сфера минимального радиуса одновременно оказалась вписанной в обе поверхности, то имеет место частный случай пересечения поверхностей, описываемый теоремой Монжа. При этом дальнейшее использование метода сфер теряет смысл. Проекция линии пересечения строится значительно проще: находятся точки пересечения очерков поверхностей и попарно соединяются прямыми линиями крест-накрест.
5. Полученные точки соединить плавной кривой линией.
6. Выполнить обводку проекции поверхностей с учетом видимости.
|
|
|


