 |
Примеры использования метода вспомогательных сфер
|
|
|
|
Пример 1. Построение проекции линии пересечения конуса и цилиндра приведено на рис. 4.
Характерные точки – 1 и 2 совпадают с точками пересечения очерков поверхностей.
Вначале вычертим вспомогательную сферу минимального радиуса с центром в точке О2. Радиус сферы определим построением точки ее касания с конусом (А2), для чего из центра сферы проведем перпендикуляр к образующей конуса. Построив линии пересечения сферы с обеими поверхностями, находим их общую точку 3.
Затем строим сферу немного большего радиуса и находим общую точку 4.
Проекции линий пересечения вспомогательных сфер с заданными поверхностями образуют 2 семейства параллельных прямых, перпендикулярных соответствующим проекциям осей вращения поверхностей. Пересечение прямой линии одного семейства с соответствующей прямой линией другого семейства и дает нам искомые проекции точек, принадлежащих линии пересечения поверхностей.
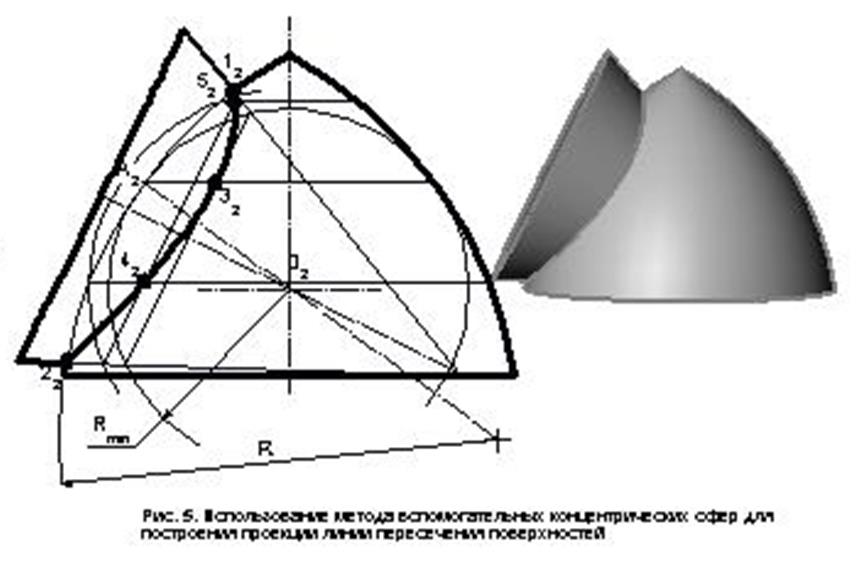
Пример 2. Построение проекции линии пересечения поверхностей тора и конуса (рис. 5).
Построение проводится аналогично описанному в примере 1.
Отличие заключается лишь в вычерчивании вспомогательной сферы минимального радиуса. Точка касания поверхностей сферы и тора (А2) лежит на линии, проходящей через центры дуг окружностей, являющихся образующими данных поверхностей.
Пример 3. Построение проекции линии пересечения двух усеченных конусов (рис. 6).
Построив сферу минимального радиуса, мы обнаружили, что поверхности обоих конусов описаны вокруг этой сферы. Такой случай описывается теоремой Монжа, согласно которой линия пересечения поверхностей распадается на 2 плоские кривые. Строим линии касания обоих конусов со сферой минимального радиуса и находим проекцию их общих точек (32). Затем соединяем отрезками прямых точки пересечения очерков конусов 12 и. 22 с точкой 3 2. Полученные отрезки прямых линий и есть проекция линии пересечения заданных поверхностей.
|
|
|


Задача №3
1. Изобразить на свободном месте эпюра поверхность Р, ограниченную построенной линией пересечения (допускается дополнительные построения производить прямо на чертеже к задаче №2).
2. Для построения приближенной развертки поверхности Р следует аппроксимировать линейчатую (цилиндрическую или коническую) поверхность гранной поверхностью (призматической или пирамидоидальной). Для учебной работы достаточно применить 12-гранную поверхность.
3. На свободном месте провести линию:
· вертикальную или горизонтальную прямую развернутого нормального сечения – для построения развертки цилиндрической поверхности. Длину линии можно посчитать по формуле 2πR (где R – радиус цилиндра) или первоначально взять произвольную длину;
· 
|
где R – радиус основания конуса, L – длина его образующей,
или вначале провести дугу радиусом L произвольной величины.
4. В зависимости от выбранного способа построения линии развертки, или разделить ее на 12 равных отрезков – в случае фиксированной величины линии, или на линии последовательно отложить 12 отрезков, равных ширине граней гранной поверхности.
5. Через каждый конец отрезка провести прямые линии:
· перпендикулярно к исходной линии – для построения развертки цилиндрической поверхности;
· к центру дуги – для построения развертки поверхности конуса.
6. На проведенных линиях отложить соответствующие длины каждого ребра гранной поверхности.
|
|
|
При построении развертки цилиндрической поверхности длины ребер каждой можно измерять непосредственно на поверхности цилиндра, аппроксимированного призмой, так как все они параллельны фронтальной плоскости проекций и, следовательно, проецируются на плоскость π2 в натуральную величину.
Однако длины ребер пирамиды, аппроксимирующей коническую поверхность, за исключением боковых граней, не параллельны плоскости проекций. Поэтому необходимо определять их натуральную величину. Используем метод вращения вокруг проецирующей прямой, в качестве которой возьмем ось вращения конуса.
7. Соединить плавной линией построенные точки (тип линии – сплошная основная). Провести ось симметрии развертки. Допустимо построить половину развертки. Обозначить развертку в соответствии с ГОСТ 2.109-68.
|
|
|


