 |
Методические рекомендации по выполнению контрольной работы.
|
|
|
|
Правила выполнения и оформления
КонтрольнОЙ работЫ
1. На титульном листе работы должны быть разборчиво написаны фамилия и инициалы студента, номер варианта (соответствует последней цифре в номере зачётной книжки)
2. Решения задач необходимо располагать в порядке номеров, указанных в задании, сохраняя номера задач.
3. Перед решением задачи следует выписать полностью ее условие.
4. Решение задач излагать подробно и аккуратно, объясняя все действия и делая необходимые чертежи.
5. Если после проверки контрольной работы поставлена отметка "Неудовлетворительно", необходимо в этой же тетради сделать работу над ошибками и представить работу для повторной проверки. Это необходимо сделать в кратчайшие сроки.
6. Студент допускается к экзамену (зачету) по математике при наличии у него контрольной работы с отметкой не ниже удовлетворительной.
Вариант 0.
Задание 1. Найти неопределенные интегралы.
а)  ; б)
; б)  .
.
Задание 2. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а) 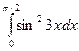 ; б)
; б) 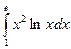
Задание 3.Найти общее решение дифференциальных уравнений.
а)  ; б)
; б) 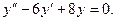
Задание 4. Составьте таблицy истинности. Упростите выражение и сделайте вывод об их истинности: 
Задание 5. Найти множества 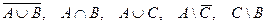 , если
, если 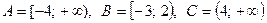 .
.
Задание 6. Доказать с помощью кругов Эйлера тождество 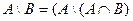 .
.
Задание 7. В классе 35 учеников. Из них 20 занимаются в математическом кружке, 11 – в биологическом, 10 ребят не посещают эти кружки. Сколько биологов увлекаются математикой?
Задание 8. Студент разыскивает нужную ему формулу в трёх справочниках. Вероятность того, что формула есть в первом справочнике, равна 0,6, во втором -0,7, в третьем -0,8. Найдите вероятность того, что формула есть
|
|
|
А) хотя бы в одном справочнике, б) хотя бы в одном справочнике.
Задание 9. Вероятность того, что клиент банка не вернёт заем в период экономического роста, равная 0,04, а период экономического кризиса-0,13.
Предположим, что вероятность того, что начнётся период экономического роста, равна 0,65. Зная, что клиент банка не вернул
полученный кредит, найти вероятность того, что наблюдается экономический кризис.
Задание10. Имеются следующие данные о размерах основных фондов (в млн. руб.) 30 предприятий:
4,2; 2,4; 4,9; 6,7; 4,5; 2,7; 3,9; 2,1; 5,8; 4,0; 2,8; 7,3; 4,4; 6,6; 2,0; 6,2; 7,0; 8,1; 0,7; 6,8; 9,4; 7,6; 6,3; 8,8; 6,5; 1,4; 4,6; 2,0; 7,2; 9,1.
а) постройте интервальную таблицу частот с шириной интервала 2 млн. руб.; б) постройте гистограмму.
Вариант № 1.
Задание 1. Найти неопределенные интегралы.
а)  ; б)
; б)  .
.
Задание 2. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а)  ; б)
; б) 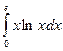 .
.
Задание 3.Найти общее решение дифференциальных уравнений
а)  ; б)
; б) 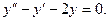
Задание 4. Составьте таблицy истинности. Упростите выражение и сделайте вывод об их истинности: 
Задание 5. Найти множества 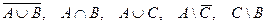 , если
, если
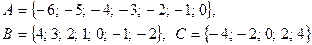
Задание 6. Доказать с помощью кругов Эйлера тождество 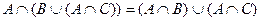
Задание 7. Каждый из членов команды играет либо в футбол, либо в хоккей, либо в футбол и в хоккей. Сколько человек в команде, если известно, что 18 человек играют в обе игры, 23 человека играют в футбол, 21 – в хоккей?
Задание 8. Два стрелка сделали по одному выстрелу по мишени. Вероятность попадания для одного из стрелков равна 0,6. Для другого -0,7. Найдите вероятность того, что
хотя бы один из стрелков попадёт в мишень.
Задание 9. Два кирпичных завода поставляют одну и туже марку кирпича на стройку. Первый завод поставляют каждый день 3000 кирпичей, второй -5000 кирпичей. Известно, что 80 % продукции первого завода и 96% продукции второго завода является стандартной. Найти вероятность того, что наугад выбранный из ежедневной поставки кирпич окажется нестандартным?
|
|
|
Задание10.
Задана выборка из генеральной совокупности значений дискретной случайной величины Х: 3, 3, 2, 2, 4, 1, 2, 3, 2, 3, 4, 1, 2, 4, 3, 1, 3, 4, 2, 1, 2, 2, 3, 3, 3.Составьте таблицу частот и постройте полигон.
Вариант № 2.
Задание 1. Найти неопределенные интегралы.
а)  ; б)
; б)  .
.
Задание 2. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а)  ; б)
; б) 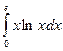 .
.
Задание 3.Найти общее решение дифференциальных уравнений.
а  ; б)
; б) 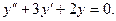
Задание 4. Составьте таблицy истинности. Упростите выражение и сделайте вывод об их истинности: 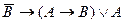
Задание 5. Найти множества 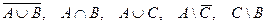 , если
, если
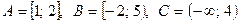
Задание 6. Доказать с помощью кругов Эйлера тождество  .
.
Задание 7. В лицее при некотором университете 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке – 8, 3 спортсмена посещают и драмкружок, и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке?
Задание 8.Правовой центр получил приглашение для оказания юридических услуг от двух фирм. Вероятность получения заказа от фирмы А предположительно 0,54,от фирмы В - 0,62.С какой вероятностью адвокаты правового центра получат не менее одного заказа?
Задание 9.Экономист-аналитик условно подразделяет экономическую ситуацию в стране на «хорошую», «посредственную» и «плохую» и оценивают их вероятности для данного момента времени в 0,15; 0,70 и 0,15 соответственно. Некоторый индекс экономического состояния возрастает с вероятностью 0,6, когда ситуация «хорошая»; с вероятностью 0,3, когда ситуация «посредственная», и с вероятностью 0,1, когда ситуация «плохая». Найти вероятность возрастания этого индекса.
Задание 10. С целью анализа вкладов населения в один из банков районного центра было проведено выборочное исследование 56-ти клиентов. Сумма вкладов, внесённых клиентами в течение месяца поместили в интервальный вариационный ряд:
| Сумма вкладов в у.е. | до 500 | 500-1000 | 1000-2000 | 2000-3000 | свыше 2000 |
| Количество вкладчиков |
Преобразуйте данную таблицу в интервальную таблицу частот и постройте гистограмму
|
|
|
Вариант № 3.
Задание 1. Найти неопределенные интегралы.
а) 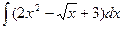 ; б)
; б) 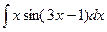 ;
;
Задание 2. Вычислить определенные интегралы по формуле Ньютона-
Лейбница. а)  ; б)
; б) 
Задание 3.Найти общее решение дифференциальных уравнений.
а)  ; б)
; б) 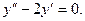
Задание 4. Составьте таблицy истинности. Упростите выражение и сделайте вывод об их истинности: 
Задание 5. Найти множества 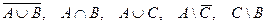 , если
, если
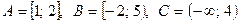
Задание 6. Доказать с помощью кругов Эйлера тождество 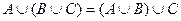 .
.
Задание 7. В лицее при некотором университете 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке – 8, 3 спортсмена посещают и драмкружок, и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке?
Задание 8. Два станка работают независимо друг от друга. Вероятность бесперебойной работы первого станка в течение времени t равна 0,9, а второго - 0,8.Определите вероятность бесперебойной работы хотя бы одного из двух станков в течение времени t.
Задание 9. В каждой из трёх урн содержится 6 чёрных и 4 белых шара. Из первой урны наудачу извлечён один шар и переложен во вторую урну, после чего из второй урны наудачу извлечён один шар и переложен в третью урну.
Найти вероятность того, что шар, наудачу извлечённый из третьей урны,
окажется белым.
Задание 10.При изучении некоторой дискретной случайной величины в результате 40 независимых наблюдений получена выборка:
10, 13, 10, 9, 9, 12, 12, 6, 7, 9;
8, 9, 11, 9, 14, 13, 9, 8, 8, 7;
10, 10, 11, 11, 11, 12, 8, 7, 9, 10;
14, 13, 8, 8, 9, 10, 11, 11, 12, 12.
Требуется: а) составить вариационный ряд; б) составить таблицу частот; в) построить полигон.
Вариант № 4.
Задание 1. Найти неопределенные интегралы.
а) 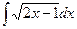 ; б)
; б)  .
.
Задание 2. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а)  ; б)
; б) 
Задание 3.Найти общее решение дифференциальных уравнений
а) 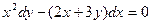 б)
б) 
Задание 4. Составьте таблицy истинности. Упростите выражение и сделайте вывод об их истинности: 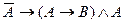
|
|
|
Задание 5. Найти множества 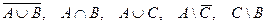 , если
, если

Задание 6. Доказать с помощью кругов Эйлера тождество 
Задание 7. В некоторой школе есть класс увлечённых ребят. Семь учеников из этого класса увлекаются математикой, шесть – физикой, пять – астрономией. Четверо из них увлекаются математикой и физикой, трое – математикой и астрономией, двое – физикой и астрономией. Сколько учеников в этом классе?
Задание 8. Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго - 0,8.
Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.
Задание 9. Два кирпичных завода поставляют одну и туже марку кирпича на стройку. Первый завод поставляют каждый день 3000 кирпичей, второй -5000 кирпичей. Известно, что 80 % продукции первого завода и 96% продукции второго завода является стандартной. Найти вероятность того, что наугад выбранный из ежедневной поставки кирпич окажется нестандартным?
Задание 10. Пятьюдесятью абитуриентами на вступительных экзаменах получены следующие количества баллов:
12, 14, 19, 15, 14, 18, 13, 16, 17, 12,
20, 17, 15, 13, 17, 16, 20, 14, 14, 13,
17, 16, 15, 19, 16, 15, 18, 17, 15, 14,
16, 15, 15, 18, 15, 15, 19, 14, 16, 18,
18, 15, 15, 17, 15, 16, 16, 14, 14, 17.
Требуется: а) составить вариационный ряд; б) составить таблицу частот; в) построить полигон частот; г) определите числовые характеристики.
Вариант № 5.
Задание 1. Найти неопределенные интегралы.
а) 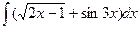 ; б)
; б)  .
.
Задание 2. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а) 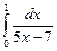 ; б)
; б)  .
.
Задание 3.Найти общее решение дифференциальных уравнений
а) 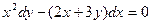 б)
б) 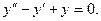
Задание 4. Составьте таблицy истинности. Упростите выражение и сделайте вывод об их истинности: 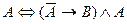
Задание 5. Найти множества 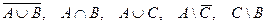 , если
, если

Задание 6. Доказать с помощью кругов Эйлера тождество 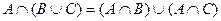
Задание 7.Секретарь факультета программирования составил отчёт, в котором сказано, что 100 абитуриентов английский язык в школе изучали 50 человек, немецкий – 23, а французский – 30. С английским и французским языками знакомы 8 абитуриентов, с французским и немецким – 10, а с английским и немецким – 20. Все три языка изучали 5 абитуриентов. Почему секретарь получил выговор за этот отчёт? Докажите, что в отчёте имеется ошибка.
Задание 8. В первой урне содержится 10 шаров, из них 8 белых, во второй урне 20 шаров, из них 4 белых. Из каждой урны наудачу извлекли по одному шару, а затем из этих двух шаров наудачу взят один шар. Найти вероятность того, что взят белый шар.
Задание 9.Вероятность того, что клиент банка не вернёт заем в период экономического роста, равная 0,04, а период экономического кризиса-0,13.
|
|
|
Предположим, что вероятность того, что начнётся период экономического роста, равна 0,65. Зная, что клиент банка не вернул
полученный кредит, найти вероятность того, что наблюдается экономический кризис.
Задание 10.
При изучении некоторой дискретной случайной величины в результате 40 независимых наблюдений получена выборка:
10, 13, 10, 9, 9, 12, 12, 6, 7, 9;
8, 9, 11, 8, 14, 13, 9, 8, 8, 7;
7, 10, 11, 11, 11, 6, 8, 7, 9, 10;
14, 13, 6, 8, 9, 11, 11, 10, 12, 12.
Требуется: а) составить вариационный ряд; б) составить таблицу частот; в) построить полигон
Вариант № 6.
Задание 1. Найти неопределенные интегралы.
а) 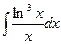 ; б)
; б)  .
.
Задание 2. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а) 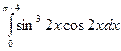 ; б)
; б)  .
.
Задание 3.Найти общее решение дифференциальных уравнений
а) 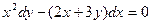 ; б)
; б) 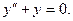
Задание 4. Составьте таблицy истинности. Упростите выражение и сделайте вывод об их истинности: 
Задание 5. Найти множества 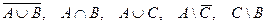 , если
, если
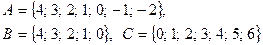
Задание 6. Доказать с помощью кругов Эйлера тождество 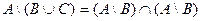
Задание 7. Из 100 студентов факультета программирования 42 посещают спортивные секции, 30 – занятия по изобразительному искусству, а 28 – кружки художественной самодеятельности. На занятия по изобразительному искусству и спорту успевают ходить 5 студентов. Спортом и художественной самодеятельностью занимаются 10, изобразительным искусством и художественной самодеятельностью – 8, а сразу все три увлечения имеют три студента. Сколько студентов не занимаются ни в каких секциях?
Задание 8. Вероятность того, что клиент банка не вернёт заем в период экономического роста, равная 0,04, а период экономического кризиса-0,13.
Предположим, что вероятность того, что начнётся период экономического роста, равна 0,65. Зная, что клиент банка не вернул
полученный кредит, найти вероятность того, что наблюдается экономический кризис.
Задание 9.Два стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7, а для второго - 0,8.
Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.
Задание 10. Тридцатью абитуриентами на вступительных экзаменах получены следующие количества баллов:
12, 16, 19, 15, 14, 18, 13, 16, 14, 12,
20, 17, 12, 13, 19, 16, 20, 15, 14, 13,
17, 16, 15, 19, 16, 17, 18, 17, 15, 18.
Требуется: а) составить вариационный ряд; б) составить таблицу частот; в) построить полигон частот; г) определите числовые характеристики.
Вариант № 7.
Задание 1. Найти неопределенные интегралы.
а)  ; б)
; б)  .
.
Задание 2. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а)  ; б)
; б) 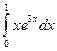 .
.
Задание 3.Найти общее решение дифференциальных уравнений
а) 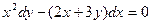 ; б)
; б) 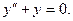
Задание 4. Составьте таблицy истинности. Упростите выражение и сделайте вывод об их истинности: 
Задание 5. Найти множества 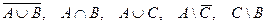 , если
, если
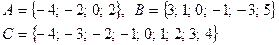
Задание 6. Доказать с помощью кругов Эйлера тождество 
Задание 7. В ожесточённом бою из 100 пиратов потеряли по одному глазу – 70, по одному уху – 75, по одной руке – 80, по одной ноге – 85, пиратов. Каково минимальное число пиратов, потерявших одновременно глаз, ухо, ногу и руку?
Задание 8. Отдел технического контроля проверяет изделия на стандартность.
Вероятность того, что изделие стандартное, равна 0,9. Найти вероятность того, что из двух проверенных изделий только одно стандартное.
Задание 9. В каждой из трёх урн содержится 6 чёрных и 4 белых шара. Из первой урны наудачу извлечён один шар и переложен во вторую урну, после чего из второй урны наудачу извлечён один шар и переложен в третью урну.
Найти вероятность того, что шар, наудачу извлечённый из третьей урны,
окажется белым.
Задание 10. При изучении некоторой дискретной случайной величины в результате 40 независимых наблюдений получена выборка:
10, 13, 16, 9, 9, 12, 10, 6, 7, 9;
8, 9, 11, 8, 15, 13, 9, 8, 8, 7;
7, 10, 12, 11, 11, 16, 8, 7, 9, 10;
14, 13, 6, 8, 9, 11, 13, 10, 12, 12.
Требуется: а) составить вариационный ряд; б) составить таблицу частот; в) построить полигон.
Вариант № 8.
Задание 1. Найти неопределенные интегралы.
а) 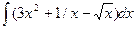 ; б)
; б)  .
.
Задание 2. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а)  ; б)
; б) 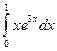 .
.
Задание 3.Найти общее решение дифференциальных уравнений
а) 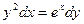 ; б)
; б) 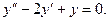
Задание 4. Составьте таблицy истинности. Упростите выражение и сделайте вывод об их истинности: 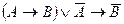
Задание 5. Найти множества 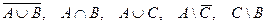 , если
, если

Задание 6. Доказать с помощью кругов Эйлера тождество 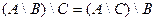
Задание 7. В классе 40 учеников. Из них по русскому языку имеют «тройки» 19 человек, по математике – 17 человек и по физике – 22 человека. Только по одному предмету имеют «тройки»: по русскому языку – 4 человека, по математике – 4, по физике – 11. Семь человек имеют «тройки» и по математике, и по физике, из них пятеро имеют «тройки» и по русскому языку. Сколько человек учатся без «троек»? Сколько человек имеют «тройки» по двум из трёх предметов?
Задание 8.Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие окажется высшего сорта равна 0,8. Найти вероятность того, что из трёх проверенных изделий только 2 изделия высшего сорта.
Задание 9.Экономист-аналитик условно подразделяет экономическую ситуацию в стране на «хорошую», «посредственную» и «плохую» и оценивают их вероятности для данного момента времени в 0,15; 0,70 и 0,15 соответственно. Некоторый индекс экономического состояния возрастает с вероятностью 0,6, когда ситуация «хорошая»; с вероятностью 0,3, когда ситуация «посредственная», и с вероятностью 0,1, когда ситуация «плохая». Найти вероятность возрастания этого индекса.
Задание 10.Тридцатью абитуриентами на вступительных экзаменах получены следующие количества баллов:
132, 16, 19, 15, 19, 18, 13, 16, 14, 11,
20, 17, 12, 13, 19, 16, 20, 19, 14, 13,
17, 18, 15, 19, 16, 17, 18, 17, 15, 18.
Требуется: а) составить вариационный ряд; б) составить таблицу частот; в) построить полигон частот; г) определите числовые характеристики
Вариант № 9.
Задание 1. Найти неопределенные интегралы.
а)  ; б)
; б) 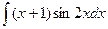 .
.
Задание 2. Вычислить определенные интегралы по формуле Ньютона-
Лейбница.
а) 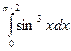 ; б)
; б) 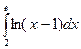
Задание 3.Найти общее решение дифференциальных уравнений
а)  ; б)
; б) 
Задание 4. Составьте таблицy истинности. Упростите выражение и сделайте вывод об их истинности: 
Задание 5. Найти множества 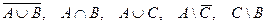 , если
, если

Задание 6. Доказать с помощью кругов Эйлера тождество 
Задание 7. Группа грабителей посетила 18 квартир. Из 12 вынесли телевизор, из 10 – видеомагнитофон, Из 6 – музыкальный центр, из 5 – только телевизор и видеомагнитофон, из 2 – видеомагнитофон и музыкальный центр, из 3 – телевизор и музыкальный центр, из 2 квартир не вынесли ничего. Из сколько квартир украли все три предмета.
Задание 8. В каждой из трёх урн содержится 6 чёрных и 4 белых шара. Из первой урны наудачу извлечён один шар и переложен во вторую урну, после чего из второй урны наудачу извлечён один шар и переложен в третью урну.
Найти вероятность того, что шар, наудачу извлечённый из третьей урны,
окажется белым.
Задание 9. Вероятность того, что клиент банка не вернёт заем в период экономического роста, равная 0,04, а период экономического кризиса-0,13.
Предположим, что вероятность того, что начнётся период экономического роста, равна 0,65. Зная, что клиент банка не вернул
полученный кредит, найти вероятность того, что наблюдается экономический кризис.
Задание 10. При изучении некоторой дискретной случайной величины в результате 40 независимых наблюдений получена выборка:
14, 12, 16, 11, 9, 12, 14, 6, 7, 9;
8, 9, 11, 8, 15, 13, 9, 6, 8, 7;
8, 10, 12, 9, 12, 16, 8, 7, 9, 10;
14, 13, 6, 8, 9, 11, 13,8, 12, 12.
Требуется: а) составить вариационный ряд; б) составить таблицу частот; в) построить полигон.
Методические рекомендации по выполнению контрольной работы.
1. Найти неопределенные интегралы.
а)  .
.
Решение.
Это интеграл от алгебраической суммы функций. Применяя свойства интеграла, получим:
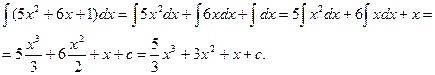
Проверим результат дифференцированием:

б) 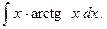
Используем метод интегрирования по частям.
Обозначим через 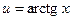 , тогда
, тогда 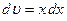 .
.
Находим 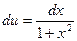 и
и 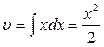 . Тогда
. Тогда

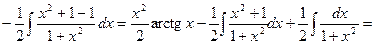
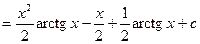
2. Вычислить определенные интегралы по формуле Ньютона-Лейбница.
а) 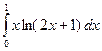 .
.
Решение.
Примем за 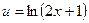 , тогда
, тогда  .
.
Найдем  ,
, 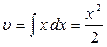 . Тогда
. Тогда




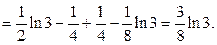
б) Вычислить определенный интеграл 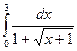 .
.
Решение.
Пусть 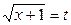 , тогда
, тогда 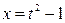 ,
,  .
.
Если х =0, то 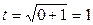 , если х =3, то
, если х =3, то 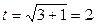 . Тогда
. Тогда
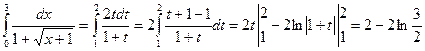 .
.
3.Найти общее решение дифференциальных уравнений
а)  ; б) y'' − 6 y' + 5 y = 0.
; б) y'' − 6 y' + 5 y = 0.
а)Решить уравнение:  .
.
Решение.
Разделяем переменные:

 .
.
Интегрируя, получаем 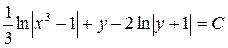
б) Решить дифференциальное уравнение y'' − 6 y' + 5 y = 0.
Решение.
Запишем сначала соответствующее характеристическое уравнение:
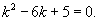
Корни данного уравнения равны k 1 = 1, k 2 = 5. Поскольку корни действительны и различны, общее решение будет иметь вид:

где C 1 и C 2 − произвольные постоянные.
4.Составьте таблицy истинности. Упростите выражение и сделайте вывод об их истинности: 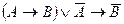
Решение:
Используя последовательно основные равносильности, получим:
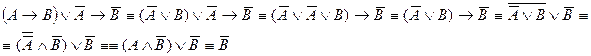
Таблица истинности:

| 
| 
| 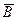
| 
| 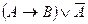
| 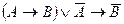
|
Истинные и ложные значения четвёртой и последней колонок совпадают.
5. Найдите множества 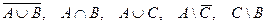 , если
, если 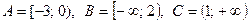
Решение:
Отметим точки на числовой прямой, соблюдая включаемость точек в множество.
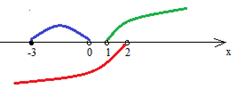
Применяя определения, получаем:
1) т.к.  , то
, то 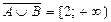 (выбираем те точки, которые не входят в объединение множеств А и В);
(выбираем те точки, которые не входят в объединение множеств А и В);
2) 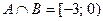 (те точки, которые принадлежат обоим отрезкам);
(те точки, которые принадлежат обоим отрезкам);
3) 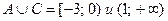 (те точки, которые принадлежат либо множеству А, либо множеству С);
(те точки, которые принадлежат либо множеству А, либо множеству С);
4) т.к.  , тогда
, тогда 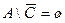 (точки множества
(точки множества  исключают все точки
исключают все точки
множества А);
5) 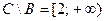 (точки, которые принадлежат множеству С, но не принадлежат множеству В).
(точки, которые принадлежат множеству С, но не принадлежат множеству В).
6.Доказать с помощью кругов Эйлера тождество 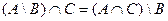 .
.
Решение:
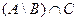

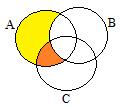

Области более темного цвета совпадают.
7. В группе 30 человек. 20 из них каждый день пользуются метро, 15 – автобусом, 23 – троллейбусом, 10 – и метро, и троллейбусом, 12 – и метро, и автобусом, 9 – и троллейбусом, и автобусом. Сколько человек ежедневно пользуется всеми тремя видами транспорта?
Решение:

М- множество студентов, пользующихся метро
А- множество студентов, пользующихся автобусом
Т- множество студентов, пользующихся троллейбусом
U- множество студентов группы
m(U) = 30
m(M) =20
m(А) = 15
m(Т) =23
m(М 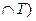 = 10
= 10
m (М 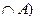 = 12
= 12
m (Т 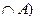 = 9
= 9
m (М  =?
=?
Для решения опять воспользуемся кругами Эйлера.
Пусть х человек пользуется всеми тремя видами транспорта.
Тогда пользуются только метро и троллейбусом (10–х) человек,
только автобусом и троллейбусом (9–х) человек, только метро и автобусом (12–х) человек.
Найдем, сколько человек пользуется одним только метро:
20 – (12 – х) – (10 – х) – х = х – 2.Аналогично получаем: (х – 6) ч. – только автобусом, (х + 4) ч. – только троллейбусом, так как всего 30 человек, составляем уравнение:
х + (12 – х) + (9 – х) + (10 – х) + (х + 4) + (х – 2) + (х – 6) = 30,
отсюда х = 3.
8.В урне содержится 5 чёрных и 6 белых шаров. Случайным образом вынимают 4 шара. Найти вероятность того, что среди них имеется хотя бы один белый шар.
Решение.
Испытание – вынимают 4 шара из 11.
Событие  – среди вынутых шаров хотя бы один белый.
– среди вынутых шаров хотя бы один белый.
Этому событию удовлетворяют следующие сочетания шаров: 1 белый и 3 чёрных (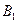 ), 2 белых и 2 чёрных (
), 2 белых и 2 чёрных (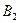 ), 3 белых и 1 чёрный (
), 3 белых и 1 чёрный (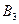 ), 4 белых (
), 4 белых (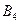 ).
).
Здесь событие  определяется словами «хотя бы один» и прямое решение приводит к сложным вычислениям. Проще сначала найти вероятность противоположного события и затем по формуле
определяется словами «хотя бы один» и прямое решение приводит к сложным вычислениям. Проще сначала найти вероятность противоположного события и затем по формуле 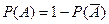 вычислить вероятность искомого события.
вычислить вероятность искомого события.
Рассмотрим противоположное событие 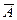 – среди вынутых шаров нет ни одного белого. Значит все вынутые 4 шара чёрные.
– среди вынутых шаров нет ни одного белого. Значит все вынутые 4 шара чёрные.
n: Сколькими способами можно вынуть 4 шара из 11.
m: Сколькими способами можно вынуть 4 чёрных шара.
Используя формулы комбинаторики, получим:
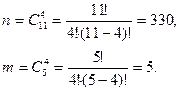
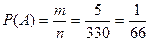 ,
, 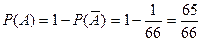 .
.
Вероятность того, что среди четырёх вынутых шаров нет ни одного белого равна 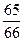 . Ответ:
. Ответ: 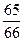 .
.
9.В монтажном цехе к устройству присоединяется электродвигатель. Электродвигатели поставляются тремя заводами-изготовителями. На складе имеются электродвигатели этих заводов соответственно в количестве 19, 6 и 11 штук, которые могут безотказно работать до конца гарантийного срока с вероятностями соответственно 0,85, 0,76 и 0,71. Рабочий берет случайно один электродвигатель и монтирует его к устройству. Найти вероятности того, что смонтированный и работающий безотказно до конца срока электродвигатель поставлен соответственно первым, вторым или третьим заводом–изготовителем.
Решение.
Испытание – выбирают электродвигатель и проверяют его работу во время гарантийного срока.
Событие А – электродвигатель работает безотказно до конца гарантийного срока.
Гипотезы: 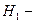 монтёр возьмёт двигатель из продукции 1-го завода;
монтёр возьмёт двигатель из продукции 1-го завода;
 монтёр возьмёт двигатель из продукции 2-го завода;
монтёр возьмёт двигатель из продукции 2-го завода;
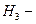 монтёр возьмёт двигатель из продукции 3-го завода.
монтёр возьмёт двигатель из продукции 3-го завода.
Из условия задачи определим вероятности: 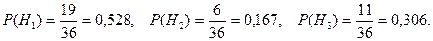
Причём 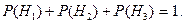
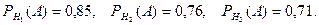

По формуле Байеса найдём условные вероятности:
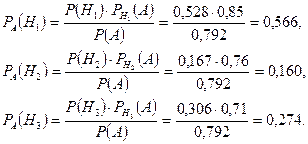
Итак, с вероятностью 0,566 можно утверждать, что смонтированный и работающий безотказно до конца гарантийного срока электродвигатель поставлен первым заводом-изготовителем; с вероятностью 0,160 – вторым; с вероятностью 0,274 – третьим.
Ответ: 0,566; 0,160; 0,274.
10.При изучении некоторой дискретной случайной величины в результате 40 независимых наблюдений получена выборка:
10, 13, 10, 9, 9, 12, 12, 6, 7, 9;
8, 9, 11, 9, 14, 13, 9, 8, 8, 7;
10, 10, 11, 11, 11, 12, 8, 7, 9, 10;
14, 13, 8, 8, 9, 10, 11, 11, 12, 12.
Требуется: а) составить вариационный ряд; б) составить таблицу частот; в) построить полигон.
Решение:
а) Выбирая различные варианты из выборки и располагая их в возрастающем порядке, получим вариационный ряд: 6, 7, 8, 9, 10, 11, 12, 13, 14.
б) Для нахождения частот 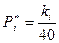 предварительно подсчитаем для каждой варианты соответствующие кратности
предварительно подсчитаем для каждой варианты соответствующие кратности 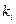 :1, 3, 6, 8, 6, 6, 5, 3, 2.
:1, 3, 6, 8, 6, 6, 5, 3, 2.
Таблица частот
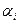
| |||||||||
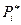
| 
| 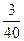
| 
| ||||||
|
|
|


