Исследование линейной импульсной системы автоматического управления

 

Задание:

1) Найти передаточные функции импульсной САУ: W ^* (z) разомкнутой системы, Ф^*(z) – замкнутой системы, Ф_е^*(z) – системы по ошибке. Параметры Т, Т₁, τ₁, К₀, γ входят в выражения передаточных функций в общем виде, т. е. в буквенном виде. Знак «*» будет относиться к передаточным функциям импульсной системы.

2) Найти интервал изменения коэффициента передачи К₀, при котором система будет устойчива: K ₀ ^” ≤ K ₀ ≤ K ^’. Для дальнейших исследований выбрать значение K ₀ =0.5 K ₀ ^’

3) Построить графики логарифмических частотных характеристик разомкнутой импульсной системы L ^* (λ) и φ^*(λ) при заданных значениях Т, Т₁, τ₁, γ и выбранном K ₀. По графикам определить запасы устойчивости системы по модулю ∆ L ^* и фазе ∆φ^*.

4) Определить ошибку системы по скорости е_ск при входном воздействии v (t)= t (скачок по скорости), а также первые два коэффициента ошибок с₀ и с₁.

5) Вычислить переходной процесс в системе при воздействии v (t)= 1[t] (скачок по положению.

 

Исходные данные:

 

Таблица 2. Анализ одноконтурного замкнутого импульса

Номер варианта	γ	T	T1	τ1
10	0.3	0.1	0.1	0,05

 

Анализируется одноконтурная замкнутая импульсная САУ, состоящая из непрерывной части (НЧ) и импульсного элемента (ИЭ), формирующего прямоугольные импульсы длительностью τ=γТ, где Т -период дискретизации, 0≤γ≤1. Исходные данные для расчетов приведены в таблице 2. Передаточная функция непрерывной части имеет вид:

 

 

Импульсный элемент представляется в виде идеального ключа и формирующего устройства с передаточной функцией:

 

 

Структурная схема системы представлена на рис. 2.1. В табл. 2 Т, Т₁, τ -постоянные времени имеют размерность секунды, К₀ - коэффициент передачи НЧ имеет размерность сек^-1 и выбирается далее.

 

Рис 2.1 Структурная схема линейной импульсной системы

1. Для нахождения передаточной функции разомкнутой импульсной САУ W ^* (z) находим передаточную функцию приведенной непрерывной части:

 

 

К W (s) применяется Z-преобразование и получается передаточная функция импульсной системы W ^* (z) = Z { W (s)}. Преобразуем W ₀ (s) к виду:

 

 

Представим W ₀ (s) в виде суммы двух слагаемых

Применим к W ₀ (s) Z-преобразование

 

 

Полученную передаточную функцию в конечном виде можно представить следующим образом:

 

 

где обозначено

 

Передаточные функции замкнутой системы находятся по выражениям:

 

2. Устойчивость системы определяется корнями характеристического уравнения замкнутой системы D^*(z) = l + W^*(z) = 0, которое для нашего случая будет иметь вид:

 

В соответствии салгебраическим критерием замкнутая система будет устойчива при выполнении неравенств

 

 

В неравенстве при известных значениях γ, Т, τ₁, Т₁ входит величина К₀. Таким образом, можно выделить отрезок значений К₀"<К₀ <К₀, при которых система будет устойчива и далее принять К₀ = 0.5К'₀. Условия устойчивости будут:

 

 

После преобразований и возврата к старым переменным получим:

 

 

Получим 0 <К₀< 7,112. Таким образом, принимаем К₀=0.5 К₀^’ =3,56.

 

1. Для построения частотных и логарифмических частотных характеристик в выражении W ^* (z) делаем замену переменной

 

 

В результате этого получим частотную характеристику W ^* (jλ) и далее логарифмическую амплитудно-частотную характеристику L ^* (λ) = 20 Lg | W ^* (jλ)| и фазочастотную характеристику φ^*(λ)= argW ^* (jλ), графики которых строятся в логарифмическом масштабе.

Передаточная функция разомкнутой системы имеет вид

 

 

Тогда можно воспользоваться следующей последовательностью команд в MATLAB:

 

>> sys=tf([0.231 0.085],[1 -(1/2.71+1) 1/2.71],1)

Transfer function:

0.231 z + 0.085

---------------------

z^2 - 1.369 z + 0.369

 

>> sys_tr=d2c(sys,'tustin')

 

Transfer function:

-0.05332 s^2 - 0.1242 s + 0.4616

--------------------------------

s^2 + 0.9218 s + 2.047e-016

 

(опция 'tustin’ предназначена для преобразования )

Получаем выражение:

 

 

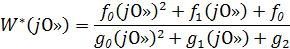
где параметры g и f видны из вышеприведенного выражения.

 

Рис 2.2

 

4. Рассматриваемая система для всех вариантов является астатической с астатизмом первого порядка и имеет следующую передаточную функцию:

 

 

В силу астатизма первого порядка в такой системе статическая ошибка всегда равна нулю, а скоростная е_ск вычисляется по формуле:

 

 

и следовательно, е_ск =1,999.

Вычислим коэффициенты ошибок. Величина С₀ =0, а коэффициент ошибки

 

 

Где  передаточная функция системы по ошибке.

Тогда получим производную:

 

 

Подставив в последнее выражение найденные ранее значения и z=1, окончательно получим С₁ =1,999.

5. При входном воздействии вида v (k) = l[k] переходный процесс в замкнутой системе можно вычислить с помощью моделирования импульсной системы в Matlab. Для этого необходимо задать передаточную функцию непрерывной части системы в tf - или zpk -форме, преобразовать ее в дискретную с помощью оператора c 2 d при заданном времени дискретизации T, а затем построить переходной процесс системы оператором step. Так же можно построить и логарифмические частотные характеристики импульсной системы - bode. Если задана передаточная функция замкнутой системы в виде:

 

 

и периодом дискретизации γ T, то получим

 

>> w0=tf([0.3 1 0],[0.3 1 1.411]) Transfer function:

 

0.1 s^2 + s

-------------------

0.1 s^2 + s + 3.738

0.2

>> w1=c2d(w0,0.24)

Transfer function:

z^2 - 0.8801 z - 0.1199

------------------------

z^2 - 0.4001 z + 0.09072

 

Sampling time: 0.24

>> step(W1)

 

Рис 2.3

 

На рис.2.4 представлена диаграмма Боде исследуемой дискретной системы с отмеченными на ней запасами устойчивости по амплитуде и фазе.

 

Рис. 2.4

 

12	Поделиться:

Воспользуйтесь поиском по сайту: