 |
А спектр биполярного сигнала
|
|
|
|
Sn = 2S0tn  , (4.4)
, (4.4)
где t0 – расстояние между импульсами. Эти спектры есть непрерывные функции частоты w.
Спектры периодических сигналов являются дискретными функциями частоты и имеют отсчетные значения в точках wn = n  . Огибающая отсчетных значений пропорциональна значениям непрерывного спектра непериодического сигнала:
. Огибающая отсчетных значений пропорциональна значениям непрерывного спектра непериодического сигнала:
Сn =  S(wn). (4.4)
S(wn). (4.4)
Если цифровой сигнал S(t) квазипериодический (а такие сигналы чаще всего и присутствуют в ЦСП) (рисунок 4.2), то его можно представить как сумму периодического сигнала ST(t) и случайного непериодического сигнала Scл(t).
 |
Рисунок 4.2 - Квазипериодический сигнал
Спектр случайного сигнала является непрерывным и по форме совпадает со спектром одиночного импульса.
Задачи:
Задача 1. Записать аналитические выражения, изобразить графически и проанализировать спектры непериодических сигналов S1(t), S2(t), S3(t), S4(t).
Решение
1. Используя (4.3) и полагая tn = T и  , найдем
, найдем
 = S0Т
= S0Т 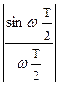 , (4.5)
, (4.5)
 = S0
= S0 
 . (4.6)
. (4.6)
Изобразим спектры графически, используя по оси абцисс безразмерную координату wТ. Как и следовало ожидать, спектр короткого импульса длительностью Т/2 в два раза шире.
 |
Рисунок 4.3 - Спектры  и
и 
2. Из (4.4) найдем спектры двух других сигналов, полагая tn =  , а t0 =
, а t0 =  и Т
и Т
 = 2 S0
= 2 S0 

 , (4.7)
, (4.7)
 = 2S0
= 2S0 

 . (4.8)
. (4.8)
 |
Рисунок 4.3 - Спектры  и
и 
У обоих сигналов S3(t) и S4(t) отсутствует постоянная составляющая. Спектры носят изменяющийся “ лепестковый ” характер. У спектра S4(w) лепестки возникают чаще, так как расстояние между импульсами больше.
Задача 2. Найти и проанализировать спектры периодических сигналов, образованных из сигналов S1(t), S2(t), S3(t), S4(t). Для сигналов S1, S2, S3 – период Т, для S4 – 2Т.
|
|
|
Решение:
Используя условие (4.4) и рисунки (4.3) и (4.4) построим спектры периодических сигналов (рисунок 4.5).Из этого рисунка можно сделать следующие выводы:
1. Сигнал S1(t), периодически продолженный, представляет собой постоянный уровень и содержит в спектре только одну составляющую при w = 0.
2. Спектр S2(w) содержит постоянную составляющую, первую, третью и все нечетные гармоники.

Рисунок 4.5 - Спектры периодических сигналов
3. Сигнал S3 содержит в спектре только нечетные гармоники. Причем преобладающей является первая.
4. Спектр сигнала S4T также как и S3T содержит отличные от нуля гармоники, которые идут с частотным интервалом в два раза меньшим, так как период этого сигнала в два раза больше. На частотах, связанных с периодом Т (w1,w2 и т.д.), амплитуды в их гармониках равны нулю.
5. Общий вывод: для передачи по каналу связи, предпочтительны сигналы S3(t) и S4 (t), т.к. они не имеют постоянной составляющей, а для выделения тактовой частоты (w1) предпочтительны сигналы S2(t) и S3(t).
Задача 3. Найти спектр квазипериодического сигнала (рисунок 4.2) в общем виде.
Решение.
Поскольку сигнал S(t) является суммой двух
S(t) = ST (t) + Sсл(t), (4.9)
то и спектр находится как сумма спектров
S(w) = ST (w) + Sсл (w). (4.10)
Спектр SТ(w) нам известен
ST(w) =  (4.11)
(4.11)
Это спектр однополярного периодического сигнала S2(t).
Оставшийся сигнал Sсл(t) содержит прямоугольные импульсы длительностью Т/2, которые расположены друг относительно друга самым произвольным образом. Поэтому при нахождении суммарного спектра, фазовые множители, определяемые временным сдвигом будут суммироваться так, что их сумма дает нуль. Поэтому спектр суммы по форме будет совпадать со спектром одиночного импульса и будет непрерывным
S4(w) ~ S2(w) (4.12)
Окончательно изобразим спектр квазипериодического сигнала как суперпозицию дискретного и непрерывного спектров
 |
Рисунок 4.6 - Спектр квазипериодического сигнала
|
|
|
Нетрудно видеть, что этот сигнал содержит тактовую частоту w, и удобен для синхронизации. Вместе с тем в сигнале большая постоянная составляющая, что не выгодно для передачи по линии.
Практическое занятие №5
Тема: Компандирование в ЦСП
Общие сведения:
 |
Назначение компандирования – это сжатие амплитудных значений отсчетов за счет неравномерного квантования (эквивалент логарифмический усилитель).
Рисунок 5.1 – Логарифмическая характеристика
Основные требования к компандеру:
1. Компрессия должна быть совмещена с кодированием;
2. Восьмиразрядная кодовая комбинация;
3. Минимизация шумов квантования;
4. Введение сигнализации.
Пути реализации:
Замена плавной логарифмической кривой на ломаную линию (рисунок 5.2).
Для упрощения процесса преобразования выбрана специальная характеристика компандирования с m=255. Эта характеристика имеет особое свойство, которое заключается в возможности хорошей ее аппроксимации ломаной линией, состоящей из восьми прямолинейных отрезков. Более того, тангенс угла наклона прямой на каждом из последующих отрезков (которые часто носят название сегментов) точно равен половине тангенса угла наклона прямой на предыдущем отрезке. Общий результат состоит в том, что большие шаги квантования имеют размеры, равные размерам меньших шагов квантования, умноженным на числа, равные степеням двух. Благодаря этому свойству кодовая комбинация, отображающая компрессированный сигнал, может быть легко преобразована (экспандирована) в линейную форму. Аналогично линейная форма легко преобразуется в компрессированную. При компрессировании больших значений дискретов наименее значащие разряды отбрасываются. Число отброшенных несущественных разрядов кодируется и включается в кодовую комбинацию компрессированного сигнала (на специально отведенных местах). Таким образом, цифровое компандирование аналогично записи чисел в логарифми
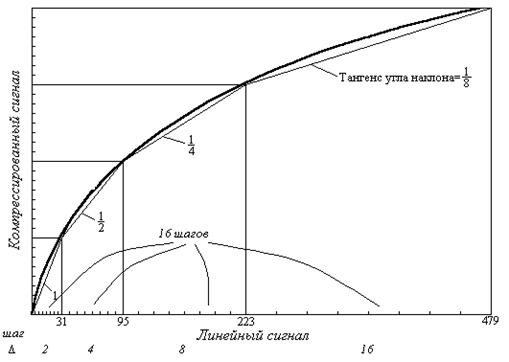 |
ческом представлении.
Рисунок 5.2 – Первые четыре сегмента аппроксимации кривой
компрессирования при m=255 отрезками прямых линий
Как показано на рисунке 5.2, каждый сегмент линейно-ломаной аппроксимации делится на шаги квантования равного размера. Для восьмиразрядных кодов комбинаций число шагов квантования, приходящихся на сегмент, составляет 16. Таким образом, восьмиразрядная кодовая комбинация, отображающая характеристику с m=255, состоит из одного разряда полярности, трех разрядов, указывающих номер сегмента, и четырех разрядов, указывающих номер шага квантования внутри сегмента (рисунок 5.3).
|
|
|
 |
Рисунок 5.3 – Формат восьмиразрядной ИКМ комбинации
с компандированием по закону m=255
В приложении А указаны конечные точки сегментов, шаги квантования и соответствующие коды сегментов и шагов квантования.
Прямое кодирование. Определение n, c, k. (алгоритм 1)
1. n=0 – положительная полярность;
n=1 – отрицательная полярность.
2. c=a; a находится из неравенства
 при наименьшем а (а принимает значения 0,1…7),
при наименьшем а (а принимает значения 0,1…7),
где x – значение дискреты.
3. k
Находится остаток:

k=b находится из неравенств:
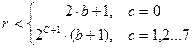 , при наименьшем b,
, при наименьшем b,
где b=0,1…15.
Декодирование (алгоритм 1)
Определение значения в средней точке между двумя шагами.

где n – целое число, полученное при соединении двоичных представлений c и k в одно число.
Преобразование на основе линейного кодирования (алгоритм 2)
Первый алгоритм дает средства для реализации ИКМ кодера с компандированием по закону m=255 путем использования 13-разрядного кодера с равномерным квантованием, вслед за которым включается цифровое логическое устройство, выполняющее функцию компрессирования. Второй алгоритм показывает, как реализовать функцию декодера, проведя сначала экспандирование кодовой комбинации, отражающей компрессированный сигнал, в 13-разрядную кодовую комбинацию линейного кода для использования в формировании дискретов на выходе.
Как и в алгоритме 1, разряд полярности определяется:
n=0 – положительная полярность;
n=1 – отрицательная полярность.
Простоту преобразования линейного кода в код с компрессированием легче всего увидеть, если сместить линейный код путем добавления значения 33 к абсолютным значениям всех дискретов. Отметим, что при таком смещении, диапазон кодирования сдвигается с 0-8159 к 33-8192. Процесс добавления может быть осуществлен непосредственно с аналоговыми дискретами перед кодированием или с помощью цифровой логики после кодирования. В любом случае обобщенная форма всех смещенных комбинаций линейного кода и соответствующих кодовых комбинаций при компрессировании представлена в таблице 5.1.
|
|
|
Таблица 5.1 – Кодирование при компрессировании по закону m=255
| Кодовые комбинации линейного кода для входного сигнала со смещением | Кодовые комбинации в результате компрессирования |
| 0 0 0 0 0 0 0 1 w x y z a 0 0 0 0 0 0 1 w x y z a b 0 0 0 0 0 1 w x y z a b c 0 0 0 0 1 w x y z a b c d 0 0 0 1 w x y z a b c d e 0 0 1 w x y z a b c d e f 0 1 w x y z a b c d e f g 1 w x y z a b c d e f g h | 0 0 0 w x y z 0 0 1 w x y z 0 1 0 w x y z 0 1 1 w x y z 1 0 0 w x y z 1 0 1 w x y z 1 1 0 w x y z 1 1 1 w x y z |
В таблице 5.2 показано, как в обратном порядке получить кодовые комбинации линейного кода со смещением из кодовых комбинаций с компрессированием. Выходной сигнал без смещения может быть получен, если вычесть 33 из кодовых комбинаций со смещением.
Таблица 5.2 - Декодирование при компрессировании по закону m=255
| Кодовые комбинации, полученные при компрессировании | Кодовые комбинации линейного кода на выходе со смещением |
| 0 0 0 w x y z 0 0 1 w x y z 0 1 0 w x y z 0 1 1 w x y z 1 0 0 w x y z 1 0 1 w x y z 1 1 0 w x y z 1 1 1 w x y z | 0 0 0 0 0 0 0 1 w x y z 1 0 0 0 0 0 0 1 w x y z 1 0 0 0 0 0 0 1 w x y z 1 0 0 0 0 0 0 1 w x y z 1 0 0 0 0 0 0 1 w x y z 1 0 0 0 0 0 0 1 w x y z 1 0 0 0 0 0 0 1 w x y z 1 0 0 0 0 0 0 1 w x y z 1 0 0 0 0 0 0 0 |
Задачи:
Задача 1. Найти комбинацию на входе кодера, и значение на выходе декодера путем алгоритма прямого кодирования (алгоритм 1), если дискреты входного сигнала равны +242 и -5987.
Решение:
Дискрет равен +242:
Так как значение дискрета положительно, то n=0.
Найдем значение c:

 , значит с=3=21+20=0 1 1.
, значит с=3=21+20=0 1 1.
Найдем значение k:

 , значит k=1=20=0 0 0 1.
, значит k=1=20=0 0 0 1.
Дискрету входного сигнала со значением +242 соответствует следующая кодовая комбинация:
| 0, 3, 1= |
Значение на выходе декодера становится равным:

что соответствует средней точке 49 шага квантования, простирающегося от 239 до 255 (Таблица А.1).
Дискрет равен -5987:
Так как значение дискрета отрицательно, то n=1.
Найдем значение c:

 , значит с=7=22+21+20=1 1 1.
, значит с=7=22+21+20=1 1 1.
Найдем значение k:

 , значит, k=7=22+21+20=0111.
, значит, k=7=22+21+20=0111.
Дискрету входного сигнала со значением -5987 соответствует следующая кодовая комбинация:
| 1, 7, 7= |
Значение на выходе декодера становится равным:
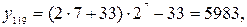
что соответствует средней точке 119 шага квантования, простирающегося от 5855 до 6111 (Таблица А.1).
Задача 2. Найти комбинацию на входе кодера, и значение на выходе декодера путем преобразования на основе линейного кодирования (алгоритм 2), если дискреты входного сигнала равны +242 и -5987.
|
|
|
Решение:
Дискрет равен +242:
Кодовая комбинация на входе, соответствующая дискрету со значением +242, смещена и получено значение +242+33=275. Арифметическое двоичное представление 275 равно:
275=256+16+2+1=28+24+21+20=0 0 0 0 1 0 0 0 1 0 0 1 1
На основе таблицы 1.1 кодирования получаем: c= 011, wxyz= 0001, а кодовая комбинация при компрессировании имеет вид:
Используя таблицу 1.2 декодирования, получим из этой комбинации с компрессированием следующую кодовую комбинацию на выходе (в линейном коде со смещением):
0 0 0 0 1 0 0 0 1 1 0 0 0
Десятичное представление кодовой комбинации равно +280 (23+24+28=8+16+256=280), что соответствует несмещенному сигналу на выходе равному +247 (+280-33=+247). Что соответствует средней точке 49 шага квантования, простирающегося от 239 до 255 (Таблица А.1).
Дискрет равен -5987:
Кодовая комбинация на входе, соответствующая дискрету со значением -5987, смещена и получено значение 5987+33=6020. Арифметическое двоичное представление 6020 равно:
6020=4096+1024+512+256+128+4=212+210+29+28+27+22=1011110000100
На основе таблицы 1.1 кодирования получаем: c= 111, wxyz= 0111, а кодовая комбинация при компрессировании имеет вид:
Используя таблицу 1.2 декодирования, получим из этой комбинации с компрессированием следующую кодовую комбинацию на выходе (в линейном коде со смещением):
1 0 1 1 1 1 0 0 0 0 0 0 0
Десятичное представление кодовой комбинации равно 6016 (27+28+29+210+212=128+256+512+1024+4096=6016), что соответствует несмещенному сигналу на выходе равному -5983 (6016-33=5983). Что соответствует средней точке 119 шага квантования, простирающегося от 5855 до 6111 (Таблица А.1).
Задача 3. Определить последовательность кодовых комбинаций для ИКМ кодера с компандированием по закону m=255, представляющую цифровой сигнал, который отображает синусоиду с частотой 1 кГц и мощностью, равной половине от максимальной.
Решение:
Поскольку частота дискретизации в стандартном ИКМ каналообразующем блоке при m=255 равна 8 кГц, для получения сигнала с частотой 1 кГц может периодически повторяться последовательность из восьми дискретов. Для удобства примем, что первый дискрет соответствует 22,5о. Вследствие этого восемь дискретов соответствуют 22,5о; 67,5о; 112,5о; 157,5о; 202,5о; 247,5о; 292,5о и 337,5о (рисунок 5.4).
Рисунок 5.4 – Восемь дискретов, изображенных на синусоиде
 |
 |
Если первый дискрет возьмем в другой точке, то получим больше значений сигнала, что нецелесообразно. Для примера взят первый дискрет соответствующий 0о (рисунок 5.5).
Рисунок 2.5 – Сравнение распределения уровней в зависимости
расположения дискретов
Для этих фаз требуется только два различных абсолютных значения дискретов, соответствующих 22,5о и 67,5о. Амплитуда синусоиды с мощностью, равной половине от максимальной, составляет  (так как
(так как  , если мощность уменьшается в 2 раза, значит, амплитуда напряжения уменьшается в
, если мощность уменьшается в 2 раза, значит, амплитуда напряжения уменьшается в  ). Таким образом, два абсолютных значения, содержащиеся в последовательности дискретов, равны:
). Таким образом, два абсолютных значения, содержащиеся в последовательности дискретов, равны:

Кодовые комбинации на входе, соответствующие дискретам со значениями 2207 и 5329, смещены и получены значения 2207+33=2240 и 5329+33=5362. Арифметические двоичные представления 2240 и 5362 равны:
2240=2048+128+64=211+27+26=0100011000000
5362=4096+1024+128+64+32+16+2=212+210+27+26+25+24+21=1010011110010
Используя таблицу 5.1, определим коды для этих двух абсолютных значений дискретов, они имеют вид, соответственно, 1100001 и 1110100. Теперь можно установить последовательность из восьми дискретов:
Таблица 5.3 – Последовательность из восьми дискретов
| Полярность | Сегмент | Шаг квантования | Фаза, соответствующая моменту дискретизации |
| 22,5о 67,5о 112,5о 157,5о 202,5о 247,5о 292,5о 337,5о |
ПРИЛОЖЕНИЕ А
В таблице А.1 представлено кодирование (декодирование) для ИКМ-преобразования по закону m=255. Здесь представлено кодирование только абсолютных величин сигнала. Разряд полярности выражается нулем для положительных сигналов и единицей – для отрицательных. Для передачи все разряды инвертируются.
Таблица А.1 – Таблица кодирования (декодирования)
для ИКМ-преобразования по закону m=255
 |
| Продолжение таблицы А1 | |||||||
| Диапазон входных амплитуд | Размер шага | Код сегмента | Код шага квантования | Номер кодовой комбинации | Амплитуда на выходе декодера | ||
| 0-1 | |||||||
| 1-3 3-5 5-7 7-9 9-11 11-13 13-15 15-17 17-19 19-21 21-23 23-25 25-27 27-29 29-31 | |||||||
| 31-35 35-39 39-43 43-47 47-51 51-55 55-59 59-63 63-67 67-71 71-75 75-79 79-83 83-87 87-91 91-95 | |||||||
| 95-103 103-111 111-119 119-127 127-135 135-143 143-151 151-159 159-167 167-175 175-183 183-191 191-199 199-207 207-215 215-223 | |||||||
| 223-239 239-255 255-271 271-287 287-303 303-319 319-335 335-351 351-367 367-383 383-399 399-415 415-431 431-447 447-463 463-479 | |||||||
| 479-511 511-543 543-575 575-607 607-639 639-671 671-703 703-735 735-767 767-799 799-831 831-863 863-895 895-927 927-959 959-991 | |||||||
| 991-1055 1055-1119 1119-1183 1183-1247 1247-1311 1311-1375 1375-1439 1439-1503 1503-1567 1567-1631 1631-1695 1695-1759 1759-1823 1823-1887 1887-1951 1951-2015 | |||||||
| 2015-2143 2143-2271 2271-2399 2399-2527 2527-2655 2655-2783 2783-2911 2911-3039 3039-3167 3167-3295 3295-3423 3423-3551 3551-3679 3679-3807 3807-3935 3935-4063 | |||||||
| 4063-4319 4319-4575 4575-4831 4831-5087 5087-5343 5343-5599 5599-5855 5855-6111 6111-6367 6367-6623 6623-6879 6879-7135 7135-7391 7391-7647 7647-7903 7903-8159 | |||||||
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №6
Тема: ИКМ-30
Общие сведения
Цифровая система передачи ИКМ-30 позволяет организовать передачу 30 каналов ТЧ. В аппаратуре ИКМ-30 для каждого канала ТЧ организуется по два выделенных сигнальных канала (СК1, СК2) для передачи сигналов управления и взаимодействия, необходимых для функционирования устройств коммутации сети. Линейный сигнал системы построен на основе сверхциклов, циклов, канальных и тактовых интервалов, как это показано на рисунке (обозначение 0/1 соответствует передаче в данном тактовом интервале случайного значения бита 0 или 1). Сверхцикл передачи (СЦ) соответствует минимальному интервалу времени, за который передается один отсчет каждого из 60 сигнальных каналов (СК) и каналов передачи аварийной сигнализации (потери сверхцикловой или цикловой синхронизации). Длительность СЦ Тсц = 2 мс. Сверхцикл состоит из 16 циклов передачи (с Ц0 по Ц15). Длительность цикла Тц = 125 мкс и соответствует интервалу дискретизации сигнала ТЧ с частотой 8 к Гц. Каждый цикл подразделяется на 32 канальных интервала длительностью Тки = 3,906 мкс. Из них 30 интервалов отводятся под передачу сигналов ТЧ (КИ1 – КИ15, КИ17 – КИ31), а два – под передачу служебной информации (КИ0 и КИ16). Каждый канальный интервал состоит из восьми интервалов разрядов (Р1 – Р8) длительностью по Тр=488 нс. Половина разрядного интервала может быть занята прямоугольным импульсом длительностью Ти=244 нс при передаче в данном разряде единицы (при передаче нуля импульс в разрядном интервале отсутствует). Интервалы КИ0 в четных циклах предназначаются для передачи циклового синхросигнала (ЦСС), имеющего вид 0011011 и занимающего интервалы Р2 – Р8. В интервале Р1 всех циклов передается информация постоянно действующего канала передачи дискретной информации (ПДИ). В нечетных циклах интервалы Р3 и Р6 КИ0 используются для передачи информации о потере цикловой синхронизации (Авар. ЦС) и снижении остаточного затухания каналов до значения, при котором в них может возникнуть самовозбуждение (Ост. зат). Интервалы Р4, Р5, Р7 и Р8 являются свободными, их занимают единичными сигналами для улучшения работы выделителей тактовой частоты. В интервале КИ16 нулевого цикла (Ц0) передается сверхцикловый сигнал вида 0000 (Р1 – Р4), а также сигнал о потере сверхцикловой синхронизации (Р6 – Авар. СЦС). Остальные три разрядных интервала свободны. В канальном интервале КИ16 остальных циклов (Ц1 – Ц15) передаются сигналы служебных каналов СК1 и СК2, причем в Ц1 передаются СК для 1-го и 16-го каналов ТЧ, в Ц2 – для 2-го и 17-го и т.д. Интервалы Р3, Р4, Р6, Р7 свободны, но в ЦСП ИКМ-30С, где для каждого канала ТЧ требуется большее число СК, они используются.
Задачи:
Задача 1.Найти скорость передачи данных во всех информационных каналах.
Задача 2.Найти скорость передачи данных в специальном канале дискретной информации.
Задача 3.Найти скорость передачи данных в свободных каналах.
Задача 4.Что произойдет, если при воздействии помехи изменится состояние(нуль перейдет в единицу и наоборот):
4.1. Р4 в КИ0 четного цикла.
4.2. Р4 в КИ0 четного цикла четыре раза подряд, как изменится при
этом Р3 в КИ0 нечетного цикла.
4.3. Р2 в КИ14 нечетного цикла.
4.4. Р2 в КИ16 3 ОГО цикла.
Решение:
1. В соответствии с временным спектром ЦСП ИКМ-30 длительность сверхцикла (СЦ) составляет 2 мс. Сверхцикл несет 16 циклов (Ц). В составе цикла 30 информационных канальныхинтервала (КИ). Канальный интервал состоит из 8 разрядныхинтервала (Р), один разрядный интервал - один бит информации. Для определения скорости передачи информации необходимо: рассчитать количество сверхциклов, переданных за одну секунду. Для этого необходимо единицу разделить на длительность сверхцикла. Умножив на 16 определим количество циклов, переданных за 1 секунду, умножив на 30, определим количество канальных интервалов, переданных за 1 секунду, и умножив на 8 разрядных интервалов, определим количество разрядных интервалов переданных за 1 секунду. Учтя, что разрядный интервал несет один бит делаем вывод: мы нашли скорость передачи данных во всех информационных каналах.
 Кбит/с.
Кбит/с.
2. В каждом цикле в нулевом канальном интервале первый разрядный интервал используется под передачу сигналов постоянно действующего канала передачи дискретной информации (ДИ). Следовательно, для определения скорости передачи информации в этом канале необходимо: рассчитать скорость передачи СЦ, умножить на 16 (Ц), 1 (Р).
 Кбит/с.
Кбит/с.
3. В КИ0 нечетных циклах под свободные позиции отведено 5 разрядных интервалов. В КИ16 нулевой цикл –3. В КИ16 с первого по шестнадцатый цикл – 4. Итого – 5*8+3+4*15 = 103 бит за сверхцикл. Следовательно, для определения скорости передачи информации в свободном канале необходимо число переданных бит разделить на время передачи
 Кбит/с
Кбит/с
4.1 Р4 в КИ0 четного цикла – один из разрядов цикловой синхронизации. При изменении вследствии действия помехи состояния этого разряда произойдет следующее:
Детектор цикловой синхронизации не опознает синхросигнал, при этом сбоя в системе не произойдет, т.к. схема детектора рассчитана на бесперебойную работу, если придет три ошибки подряд.
4.2. Р4 в КИ0 четного цикла – один из разрядов цикловой синхронизации. При изменении четыре раза подряд состояния этого разряда, вследствии действия помехи, произойдет следующее:
Детектор цикловой синхронизации не опознает синхросигнал, при этом произойдет сбой в системе. Станция будет рассылать в разрядном интервале 3 канального интервала 0 нечетного цикла сигнал «Авария цикловой синхронизации» предыдущей и последующей станциям для устранения неполадки операторами этих станций.
4.3. Р2 в КИ14 нечетного цикла – разряд 14 ОГО информационного канала, поэтому при изменении исказится информация передаваемая по этому каналу.
4.4. Р2 в КИ16 3-го цикла – разряд сигналов управления и взаимодействия (СУВ) 3ЕГО информационного канала Поэтому при его искажении изменится состояние абонентской линии (произойдет ложный вызов, отбой, набор номера и т.п.).
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №7
Тема: Линейные коды
Общие сведения:
Линейное кодирование или преобразование к коду передачи – операция, преобразующая цифровой однополярный сигнал к виду удобному для эффективной передачи по протяженной линии связи. Основные требования, предъявляемые к таким сигналам:
- низкая передаваемая мощность;
- наличие в спектре сигнала тактовой частоты;
- минимизация межсимвольных помех;
- стабильный уровень постоянной составляющей.
Межсимвольная помеха (МСП) обусловлена конечностью импульсной характеристики канала g(t). На рисунке 7.1 приведены импульсные характеристики (реакция цепи на дельта -функцию или единичный отсчет) для аналогового (а) и дискретного (б) фильтра.
 |
Как видно, если на входе системы присутствует единичный импульс, выходная реакция содержит не только этот импульс, задержанный на время t0, но и серию импульсов последействия, отстоящих от основного на время кратное времени дискретизации tg. Эти импульсы и создают МСП. Аналитически выходная реакция представляется дискретной сверткой входного сигнала Sвх к и импульсной характеристики gn
Sвых к =  .
.
Линейные коды делятся на однополярные и биполярные, каждый из которых, в свою очередь, может быть: без возврата к нулю (NRZ) и с возвратом к нулю (Rz) (рисунок 7.2).
 |
Однополярные коды содержат большую постоянную составляющую, а коды NRZ не содержат в спектре тактовой частоты. Поэтому чаще всего в практике цифровых систем передачи (проводные кабельные линии и РРЛ) используют коды RZ с чередованием полярности импульсов ЧПИ. Однако эти коды избыточны, так как в них на два цифровых состояния (0 и 1) используют три символа (0,+1,-1).
Для устранения этой избыточности применяют блочные коды. В таблице 7.1 приведены комбинации для кода ЧВЗТ когда комбинация трех символов передает четырехразрядное цифровое состояние. для того чтобы постоянная составляющая была меньше по уровню и более стабильна, столбцы 2 и 4 таблицы применяют поочередно.
К недостаткам кодов RZ ЧПИ следует отнести низкую стабильность выделяемой тактовой частоты. Такая ситуация возникает, когда в цифровой последовательности присутствует подряд много нулей. Для устранения этого применяют модифицированные коды ЧПИ (МЧПИ). В этих кодах вместо нулей добавляют определенные кодовые комбинации, которые удаляются после выделения тактовой частоты. Наиболее распространен код HDB – 3, который допускает число нулей не более трех. Комбинация 0000 заменяется на комбинацию 000V или B00V, где В и V принимают значения ±1. Правила составления кода:
1. Полярность В всегда противоположна полярности предыдущего импульса, а полярность V – совпадает.
2. Если число единиц после предыдущей замены четное, то вводится B00V, если нечетное 000V.
Другой вид кодов, при которых сохраняется тактовая частота - биимпульсные коды. Здесь каждый символ представляется одним биполярным импульсом (рисунок 7.3).
 |
Этот код называют биимпульсным. Кроме того есть относительный биимпульсный код, когда при значении “ единица ” происходит смена фаз, а при значении “нуль” – нет.
Коды CMI – сочетание ЧПИ и биимпульсных кодов. Здесь для значений сигнала “ единица ” происходит изменение полярности каждого четного импульса, а “нуль ” передается биполярным импульсом как в биимпульсных кодах.
Задачи:
Задача 1. Сравнить уровень МСП фильтра, описываемого дискретной импульсной характеристикой gк = {1, 0,3, 0,1} для цифровой импульсной последовательности 11100, передаваемой кодами:
- однополярный RZ;
- ЧПИ RZ.
Дать графическое представление происходящих процессов.
Решение:
В соответствии с выражением (7.1) находим дискретные отсчеты выходного сигнала для Sk(1)=(1,1,1,0,0), к=0,1,2,3,4,5.
Sвых(1)к= 
К=0 Sвых(1)0=S0(1) g0+ S1(1)g-1+…=1´1=1
К=1 Sвых(1)1=S0(1) g1+ S1(1)g0+S2(1)g –1+…=1´0,3+1´1=1,3
К=1 Sвых(1)2=S0(1) g2+ S1(1)g1+S2(1)g 0+…=1´0,1+1´0,3+1´1=1,4
Аналогично
Sвых(1)4=0,1
Таким образом, Sвых(1)к = {1;1,3;1,4;0,4;0,1} (7.2)
и межсимвольная помеха в канале с номерами к=3 и к=4 составляет 0,4 и 0,1 соответственно.
Находим выходной сигнал Sвых(2)к для входного сигнала
S(2)к = {1,-1,1,0,0}.
Используя (7.1), получим
Sвых(2)к={1,-0,7, 0,8, 0,2, 0,1}. (7.3)
Сравнивая (7.2) и (7.3), видим, что для сигнала с ЧПИ уровень МСП в канале с к=3 снизился по амплитуде в 2 раза.
Проведем графическое построение для первого случая, учитывая, что реакция на каждый входной единичный отсчет есть дискретная импульсная характеристика (рисунок 7.4).
 |
Sвых(1)к находим как сумму трех реакций на Sвх0, Sвх1 и Sвх2. Суммирование проводим при одинаковом значении k.
Сравнивая результаты аналитического и графического расчетов, видим, что они совпадают.
Задача 2. Заданную цифровую двоичную импульсную последовательность 111000000001101000001 преобразовать к виду, удобному для передачи с помощью кодов:
- RZ;
- RZ ЧПИ;
- ЧВЗТ;
- биимпульсный абсолютный;
- биимпульсный относительный;
- CMI;
- HDB3.
Решение:
Представим заданную цифровую последовательность в виде импульсных сигналов:

ttt
Так как tи=1/2 t, то это будет код RZ.
Применяя правила преобразования, найдем другие коды.
RZ ЧПИ
 |
4ВЗТ – разбиваем комбинацию на тетрады. Заменяем каждую на элемент троичного кода
1110, 0000, 0001, 1010, 0000, 1000
 + - 0 - - - + + 0 0 + - - - - 0 + 0
+ - 0 - - - + + 0 0 + - - - - 0 + 0
Строим код

Биимпульсный абсолютный
 |  | ||
Биимпульсный относительный
 |  | ||
СМI
 | |||||||||||
 |  | ||||||||||
 |  |  | |||||||||
HDB-3. В исходном сигнале есть серия из 8 нулей, следующих подряд. Поскольку в предыдущей пачке циклов число единиц нечетное (3), то первых четыре нуля заменяем на комбинацию 000V.
 |
|
|
|


