 |
Влияние теплового шума (броуновского движения) на показания гальванометра
|
|
|
|
Гальванометры относятся к электроизмерительным приборам высокой чувствительности. Среди гальванометров наиболее точным является зеркальный гальванометр благодаря выносной шкале.
Отделение шкалы от подвижной части инструмента позволяет измерять очень малые токи. Недостатком таких приборов является то, что их механическая часть (подвижные части), расположенная в воздушном пространстве, подвергается воздействию молекул воздуха, что вызывает случайные колебания подвижного зеркала. Однако усредненный по времени вращающий момент таких воздействий равен нулю.
Если гальванометр находится в состоянии термодинамического равновесия с окружающим воздухом, то для подвижной части прибора с одной степенью свободы выполняется закон равнораспределения по степеням свободы
|
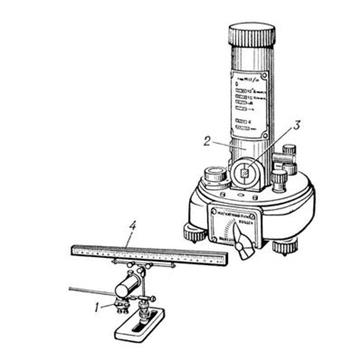
Рисунок ‑ Зеркальный гальванометр с оптическим устройством: 1 ‑ осветитель (лампа); 2 ‑ гальванометр; 3 ‑ зеркальце; 4 ‑ шкала.
,
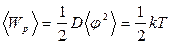где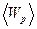 
‑ средняя потенциальная энергия; D – коэффициент упругости (модуль кручения; φ – угол отклонения от нулевого положения (
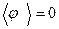). Для среднего квадрата флуктуаций угла отклонения имеем 
.
|
|
|
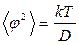Данное уравнение показывает, что электрический ток можно уверенно зафиксировать только в том случае, когда вызванное им отклонение гальванометра превышает это значение термической флуктуации. Следовательно, минимальная сила тока, которую может измерить данный гальванометр, определяется как ток Imin, вызывающий отклонение на угол, равный корню из среднего квадрата флуктуационных отклонений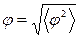 
.
Воспользовавшись соотношением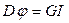 
, где G – динамическая константа гальванометра, получим 
.
Полученное соотношение оказывается справедливым и для других электромеханических систем (мембран телефонов или пьезоэлектрических преобразователей).
Другие виды шумов
Все остальные (нетепловые) виды шумов возникают в системах, содержащих источники энергии, и связаны с прохождением тока, их интенсивность пропорциональна току. Эти шумы называют неравновесными, поскольку для их поддержания необходимо наличие электрического тока, для чего требуются дополнительные источники энергии. Как правило, неравновесные шумы являются дополнительными к равновесному шуму и существенно превосходят его по интенсивности. К таким шумам относятся:
‑ дробовой шум;
‑ генерационно-рекомбинационный шум;
‑ 1/ f – шум
‑ импульсный или взрывной шум.
Дробовой шум
Возникновение дробового шума обусловлено дискретной природой носителей заряда. Конечность (квантованность) заряда приводит к статистическим флуктуациям тока. Если по сопротивлению течёт постоянный ток, то среднее число носителей заряда, протекающее по нему в единицу времени, постоянно. В то же время в каждый момент времени число носителей заряда статистически изменяется. Это вызывает флуктуации тока (прибытие каждого электрона сопровождается всплеском тока в цепи).
Соответствующий шум называют дробовым шумом.
Дробовой шум ‑ беспорядочные флуктуации напряжений и токов относительно их среднего значения в цепях радиоэлектронных устройств, обусловленные дискретностью носителей электрического заряда ‑ электронов.
|
|
|
В отличие от теплового шума, вызванного тепловым движением электронов, дробовой шум не зависит от температуры.
Дробовой шум ‑ основная составляющая внутренних шумов большинства радиоэлектронных устройств, которые приводят к искажению слабых полезных сигналов и ограничивают чувствительность усилителей.
Дробовой шум проявляется, например, в виде акустического шума в динамике радиоприёмника, в виде «снега» на экране телевизора, «травки» на радиолокационном отметчике и т. п.
Термин «дробовой шум» (а также дробовой эффект) возник в связи с тем, что благодаря нему в громкоговорителе, подключённом к выходу усилителя или радиоприёмника, появляется акустический шум, напоминающий шум сыплющихся дробинок на металлическую пластину.
В электронно-вакуумных приборах (ЭВП) дробовой шум возникает на поверхности катода вследствие статистического характера эмиссии электронов и дискретности их заряда. В наиболее простом виде он наблюдается в вакуумном диоде с плоскими электродами.
В электронной лампе акты вылета электронов с катода или попадания их на анод образуют последовательность независимых событий, происходящих в случайные моменты времени. Поэтому ток I (t), протекающий через нее, флуктуирует. То же самое происходит в транзисторе или полупроводниковом диоде, так как пролет носителей через потенциальные барьеры осуществляется независимо в случайные моменты времени.
Спектр дробовых шумов флуктуации анодного тока, обусловленных дробовым шумом тока катода, равномерен до весьма высоких значений частот (на которых становится существенной конечность времени пролёта электрона от катода к аноду).
В силу теплового разброса скоростей электронов дробовой шум всегда сопровождается флуктуациями не только тока, но и других характеристик электронного потока. Электрические шумы, родственные дробовому шуму в ЭВП, наблюдаются и в полупроводниковых приборах. В последних различают шумы, вызванные дрейфом носителей заряда, и шумы, вызванные диффузией носителей заряда.
|
|
|
Теоретический анализ дробового шума был проведен У. Шотки в 1918 г. Он показал, что если спектральная плотность квадрата этого тока равна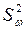 
, то для интервала частот от υ до υ + Δυ эффективный шумовой ток определится формулой
,
где I0 – среднее значение тока, постоянная составляющая.
При низких частотах (ω<<τ-1 или ν<<(2πτ)-1)
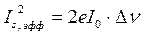
При низких частотах спектральная плотность тока постоянна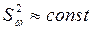 
и эффективный шумовой ток не зависит от частоты (является белым шумом). Эффективный шумовой ток пропорционален величине среднего тока и не зависит от температуры окружающей среды. Он зависит от величины тока, ширины частотной полосы и величины заряда, который переносится каждым носителем. В отличие от теплового шума в сопротивлениях, который зависит от температуры, на дробовой шум внешние условия никак не влияют. При этом спектр мощности определяется соотношением
.
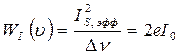Шум генерации ‑ рекомбинации
В почти беспримесном полупроводнике электроны и дырки появляются и исчезают случайным образом под влиянием процессов генерации и рекомбинации следующего вида:
свободный электрон + свободная дырка ⇔ связанный электрон в валентной зоне + энергия ⇔ свободный электрон + свободная дырка…
(знак ⇒ означает рекомбинацию, знак ⇐ означает генерацию).
В результате сопротивление образца R испытывает флуктуации δ R (t). Если через образец пропустить постоянный ток I, то на его концах возникнет флуктуирующая ЭДС: δ U (t) = I δ R (t), которая может быть обнаружена так же, как и упомянутые выше источники шума. Этот процесс называется шумом генерации ‑ рекомбинации.
Генерационно-рекомбинационный шум можно рассматривать как специфический вариант дробового шума. Ниже пороговой частоты fg спектральная мощность шума не зависит от f (белый шум), а выше ‑ она падает как 1/ f 2. Пороговая частота fg определяется средним временем жизни τ носителей заряда f = (2πτ)-1. Такая же спектральная зависимость получается, если пропустить белый шум через RС – цепочку.
|
|
|
Эффективный шумовой ток пропорционален квадрату среднего тока I 0. В полупроводниковых приборах г ‑ р шум является существенным на низких частотах.
F-шум
Один вид шума, который встречается в самых разнообразных системах (электронных, биологических, музыкальных и т.д.), и особенно в устройствах на твердом теле, приобрел широкую известность. Это является следствием его повсеместного распространения и одновременно сложности для теоретического изучения.
Это 1/ f шум, или, как его иногда называют (исторически), токовый шум, избыточный шум, фликер-шум[2] (при этом обычно имеют в виду флуктуации электронной эмиссии термокатода), полупроводниковый шум (так его называли до того, как выяснилось, что им обладают и металлы, и жидкие электролиты), контактный шум (сейчас хорошо известно, что l/ f -шум не является эффектом, связанным только с контактами).
Хотя термин l/ f -шум является общим для любого из этих явлений, из этого вовсе не следует, что существует один общий для всех этих случаев физический механизм возникновения шума такого типа. На самом деле имеющиеся данные дают возможность полагать, что причина возникновения l/ f -шума в различных случаях совершенно разная.
Название l/ f связано с тем, что спектральная плотность энергии этого шума изменяется в зависимости от частоты как 
, где значение α обычно колеблется в пределах 0,8-1,2. Эту зависимость наблюдают при понижении частоты до значений порядка 10-6 Гц. Верхний ее предел установить трудно, так как он, как правило, маскируется тепловым или каким-лидо другим шумом.
l/ f -шум ‑ явление загадочное. Он неизбежно присутствует почти во всех электронных приборах и, тем не менее, физические причины его возникновения до сих пор все еще остаются неясными. Многочисленные экспериментальные и теоретические исследования l/ f- шума выявили лишь его многогранный и неподатливый характер; после всех затраченных усилий относительно этого шума нельзя сделать почти никаких определенных выводов. Имеющиеся экспериментальные данные часто находятся в противоречии друг с другом или же остаются открытыми для интерпретации.
Существуют различные теоретические трудности при исследовании l/ f -шума, главным образом касающиеся сходимости интегралов. В настоящее время не существует ни одного вполне удовлетворительного объяснения этого явления, хотя в некоторых случаях (например, при захвате электронов оксидным слоем на полупроводнике, как это происходит в МОП-полевых[3] (металл-оксид-полупроводник) транзисторах) модели были получены. Однако такие модели не объясняют адекватно многие формы сигналов l/ f -шума.
|
|
|
Существовует научная школа, сторонники которой твердо полагают, что l/ f -шум – явление объемное, мысль, которая встречает отпор тех, кто полагает, что этот шум создается на поверхности. Возможно, единственное указание на систематичность поведения 1/ f -шума ‑ это эмпирический закон Хуга, который гласит, что уровень шума обратно пропорционален суммарному числу носителей в образце. Однако и закон Хуга не является общим. Даже в случае металлических пленок, для которых он и был первоначально сформулирован, он не всегда справедлив.
Шум 1/ f проявляет себя на низких частотах (как правило, ниже 10 кГц) в виде шума избыточного по сравнению с дробовым и с возрастающей по мере снижения частоты интенсивностью. Было обнаружено, что 1/ f шум отсутствует в проволочных[4] резисторах.
Если на непроволочный резистор подать постоянное напряжение, то помимо составляющей флуктуации тока, связанной с тепловым шумом, наблюдается еще одна составляющая. Аналогично, когда постоянный ток протекает по резистору, имеет место дополнительная случайная флуктуация в напряжении. Такая добавочная составляющая шума наблюдается у большинства резисторов при протекании постоянного тока или при подаче постоянного напряжения и характеризуется спектральной плотностью, которая зависит от частоты по закону 
, где α ‑ более или менее постоянная величина, принимающая, как правило, значения 0,8–1,2.
Спектральная зависимость такого вида наблюдается у некоторых микроволновых приборов в очень широком диапазоне, перекрывающем двенадцать порядков частоты (от 10-6 до 106 Гц) и более. На самом деле, как теперь ясно, шум, подчиняющийся закону «спектральная плотность обратно пропорциональна частоте», проявляется практически у всех материалов и элементов, используемых в электронике: у собственных полупроводников, приборов на р-n – переходах, у металлических пленок и вискеров (металлических нитях), у жидких металлов и растворов электролитов, ламп с термокатодами, у сверхпроводников и сверхпроводящих контактов Джозефсона; и обычно, где бы это явление ни наблюдалось, оно имеет общее название: 1/ f -шум.
Интересно отметить, что l/ f -шум можно представить как последовательность случайных импульсов, или более того, последовательность случайных импульсов с определенным видом функции формы импульса, для которой спектральная плотность изменяется как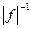 
в широком частотном диапазоне. Чтобы это выполнялось, форма импульса должна иметь вид
,
где u (t) – единичная ступенчатая функция, равная единице для t ˃ 0 и нулю, когда t ˂ 0. Трудность состоит в том, чтобы найти физический механизм, который порождает импульсы, имеющие форму, задаваемую данным выражением. В настоящее сремя такой механизм неизвестен.
Первые наблюдения l/ f -шума выполнены более восьмидесяти лет тому назад. Сейчас установлено, что l/ f -шум является универсальным типом флуктуации, он проявляется не только при измерениях в электронике, но и во все расширяющемся ряде наблюдений в самых различных сферах. Это отмечено, например, для таких явлений природы, как землетрясения, грозы, изменения уровня течения реки Нил, хотя, конечно, спектры, которые выявляются в таких случаях, нельзя считать спектрами мощности в обычном смысле этого слова.
Кроме того, некоторые биологические системы также обладают l/ f- шумом: нормальный период сердцебиения человека имеет флуктуации, спектральная плотность которых изменяется приблизительно по закону 1/ f для частот ниже 0,3 Гц, подобную же форму имеет спектр флуктуации волн мозга, в частности так называемых α-волн на электроэнцефалограммах (ЭЭГ). Хорошо известно, что нейромембраны обладают флуктуациями 1/ f.
Другой областью, где имеется l/ f -шум, является музыка. Было обнаружено, что соотношение между интенсивностью и высотой звука в классической музыке (Моцарт, Бах, Бетховен, Дебюсси), в джазовой музыке, в музыке «Битлз», а также в музыке различных эпох соответствует зависимости 1/ f.
Возможно, еще более удивительным является то, что индивидуальное восприятие музыки существенно определяется видом ее спектра. Так, три музыкальных отрывка, «скомпонованные» на основе случайных чисел и имевшие зависимости спектральных плотностей от частоты в виде l/ f 2, l/ f и l/ f 0 (белый шум), характеризовались слушателями как скучный (l/ f 2), раздражающий (белый шум) и доставляющий удовольствие 1/ f. Следует, что «хорошая» музыка имеет спектр 1/ f, вероятно, из-за того, что ее время корреляции не настолько мало, чтобы сделать ее выводящей из равновесия своей беспорядочностью, но она проливает мало света на физические механизмы возникновения такого шума.
Взрывной шум
У различных типов твердотельных приборов, таких как диоды и транзисторы на p‑n -переходах, туннельные диоды и композиционные резисторы, имеет иногда место электрический по характеру шум, проявляющийся в виде случайных «всплесков». Как правило, его обнаруживают у сравнительно небольшой части приборов определенного типа.
В своем простейшем виде данное явление проявляет себя как бистабильный сигнал ступенчатой формы, однородный по амплитуде, со случайно распределенными интервалами времени между ступенями. Изредка встречаются более сложные ступенчатые сигналы с тремя и более уровнями ступеней.
Причиной взрывного шума у p‑n-переходов с прямым смещением[5] в настоящее время принято считать дефекты кристалла в области перехода. Природа таких дефектов точно не установлена, но последние экспериментальные данные указывают на то, что это – линии скольжении и дислокации в кристаллической структуре, а не металлические примеси. Механизм, обуславливающий взрывной шум у p‑n-переходов с обратным смещением, все еще не совсем ясен.
|
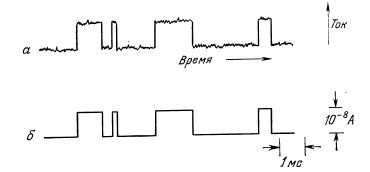
Типичный вид бистабильного взрывного шума приведен на рисунке (а). Он состоит из случайных ступенчатых импульсов, на которые наложен белый шум. Если «обрезать» этот шумовой сигнал таким образом, чтобы исключить составляющую белового шума, то он становится похожим на случайный телеграфный сигнал, как показано на рисунке (б).
|
|
|
