 |
Основное уравнение фильтрования
|
|
|
|
Пусть движущая сила процесса фильтрования D p создана столбом жидкости или поверхностными силами давления (рис. 4.16).
Рис. 4.16. Схема фильтровальной перегородки и осадка
Определим значение скорости фильтрования 
. Скорость фильтрования – это фиктивная скорость, отнесенная ко всей площади фильтрующей перегородки S. Высота слоя осадка, следовательно, и его гидравлическое сопротивление меняются с течением времени. Поэтому
по времени меняется и . Переменную скорость фильтрования определим в дифференциальной форме:
, (4.13)
где V – объем фильтрата, S – площадь фильтрующей перегородки, t – продолжительность фильтрования.
Определим эту же скорость фильтрования из гидравлического сопротивления осадка. Для расчета гидравлического сопротивления неподвижного зернистого слоя была получена следующая формула:
(4.14)
Коэффициент сопротивления определяется:
,
где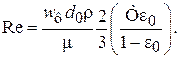 
Обычно ввиду небольшого размера пор в слое осадка, а также малой скорости движения жидкой фазы в порах можно считать, что фильтрование в пределах осадка проистекает в ламинарном режиме.
При малых значениях Re вторым членом зависимости для l можно пренебречь. С учетом этого уравнение (4.14) можно записать в виде:
|
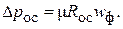(4.15)
где 
– сопротивление слоя осадка, m – вязкость фильтрата.
Аналогичная формула может быть записана и для фильтрующей перегородки:
(4.16)
Для получения полного гидравлического сопротивления фильтра, который равняется 
, необходимо сложить гидравлические сопротивления осадка и фильтрующей перегородки:
(4.17)
Для случая, если 
, из (4.17) найдем :
(4.18)
Приравнивая (4.13) и (4.18), получим:
. (4.19)
Сопротивление фильтровальной перегородки 
может быть принято постоянной величиной. Считаем, что при процессе
с образованием осадка в порах фильтровальной перегородки изменений
не происходят. В процессе фильтрования величина 
меняется непрерывно, от нуля вначале и до максимального значения в конце процесса. Установим связь с объемом фильтрата 
. Учитывая пропорциональность объемов осадка 
и фильтрата 
можно записать:
|
|
|
(4.20)
где 
– коэффициент пропорциональности,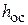 
– высота слоя осадка.
Представим сопротивление осадка в виде:
(4.21)
где 
– удельное объемное сопротивление слоя осадка. Подставляя значение 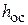из (4.20) в (4.21), получим:
(4.22)
Перепишем уравнение (4.19) с учетом (4.22):
(4.23)
Это и есть основное уравнение фильтрования. Из уравнения (4.23) видно, что производительность фильтра зависит прямо пропорционально от перепада давления D p. Производительность фильтра увеличивается
с уменьшением вязкости фильтрата и уменьшается с ростом толщины осадка 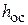и сопротивления фильтровальной перегородки.
Рассмотрим два технологических процесса фильтрования: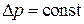 
и 
.
Пусть 
. Этот случай реализуется, когда фильтрование идет за счет сжатого воздуха или вакуумирования.
В уравнении (4.23) разделим переменную и проинтегрируем левую часть уравнения в пределах от 0 до V, а правую – от 0 до t.
(4.24)
Преобразуем второе уравнение (4.24), приведя его в удобный
для использования вид:
(4.25)
Уравнение (4.25) может быть использовано для практических целей, если известны , и . Эти величины называются константами процесса фильтрования. Их можно определить экспериментально.
На практике часто встречаются случаи, когда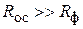 
. Тогда вторым членом левой части уравнения (4.25) можно пренебречь:
(4.26)
Уравнения (4.25) и (4.26) применимы как к сжимаемым, так
и к несжимаемым осадкам, поскольку при 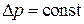значения и
в процессе фильтрования остаются постоянными.
Пусть w ф = const. Такой рабочий режим осуществляется путем нагнетания суспензии поршневым насосом. Сопротивление, встречаемое потоком фильтрата, растет с ростом толщины осадка 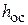. Поэтому постоянство может быть обеспечено лишь при непрерывном росте разности давлений D p. При постоянной скорости фильтрования отношение 
может быть заменено отношением 
. Тогда получим:
|
|
|
(4.27)
Уравнение (4.27) может быть приведено к виду:
(4.28)
Для случая, когда 
из (4.28) получим:
(4.29)
Из уравнения (4.28) с учетом 
найдем необходимый перепад давления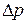 
для проведения процесса фильтрования:
(4.30)
Уравнения (4.28)–(4.30) применимы к несжимаемым осадкам.
При использовании их для сжимаемых осадков необходимо учесть зависимость удельного сопротивления осадка от D p.
|
|
|
