 |
алгоритмизация и программирование 4 глава
|
|
|
|
Число управляющих символов равно числу объектов в списке ввода-вывода. Управляющий символ имеет признак %, и одно из следующих значений:
%d – ввод - вывод целого десятичного числа (int);
%u – ввод - вывод целого без знака (unsigned);
%f – ввод - вывод числа с плавающей точкой (float и double);
%e – ввод - вывод числа в экспоненциальной форме (double и float);
%c – ввод - вывод символа (char);
%l – ввод – вывод длинного значения (long);
и другие.
При вводе и выводе необходимо строгое соответствие типа вводимого данного управляющему символу формата.
Пример форматированного ввода и вывода.
# include <stdio.h>
void main(void)
{
int my_int;
float my_float;
printf("\nВведите целое и дробное число\n");
scanf ("%d", &my_int);
scanf ("%f", &my_float);
printf ("%d %f", my_int, my_float);
}
При запуске программы она выведет на экран строку – приглашение ко вводу данных, затем при выполнении каждого scanf будет ожидать ввода данных. Пользователь должен ввести требуемое количество данных, отделяя их друг от друга пробелами или нажатием клавиши Enter. При завершении ввода данные тут же будут выведены на экран самым примитивным образом. Так, если ввести целое 5 и дробное 9.9, то строка вывода будет иметь вид:
5 9.900000
Поскольку при вводе данного функция scanf находится в состоянии ожидания ввода, рекомендуется каждый ввод предварять строкой, выводящей на экран приглашение для ввода данного, в котором пользователю подробно объясняют, что и как он должен сделать, чтобы правильно ввести данные. Этот простой прием существенно улучшит интерфейс любой программы.
При выводе данных для улучшения читабельности рекомендуется использовать некоторые приемы.
1. Управляющие символы потока, например:
\n для перевода строки при выводе;
|
|
|
\t для выполнения табуляции.
2. Произвольный текст в форматной строке для приглашения на ввод данного и для пояснений при выводе, например, функция вывода может быть записана так:
printf ("Целое = %d, Вещественное = %f\n", my_int, my_float);
Пробелы в строке текста являются значащими. Теперь, если ввести целое 5 и дробное 9.9, то строка вывода будет иметь вид:
Целое = 5, Вещественное = 9.900000
3. Модификаторы форматов. Они используются для оформления вывода. По умолчанию (без модификаторов) данные выводятся в поле минимальной ширины с точностью 6 знаков после запятой, число прижимается к правому краю поля. Выводом можно управлять.
а) Ширина поля, это строка цифр, определяющая наименьший размер поля вывода (позиционирование). Число, не входящее в поле, игнорируется.
б) Точность вывода, это две цифры, определяющие общий размер поля вывода и число знаков после запятой. Используется для вещественных чисел.
В примерах обозначим знаком ˽ пробелы, которые будут в строке вывода.
printf ("Целое = %4d, Вещественное = %5.2f\n", my_int, my_float);
Если ввести значения 10 и 2.3, то строка вывода будет иметь вид:
Целое = ˽˽10, Вещественное = ˽2.30
Если ввести значения 19951 и 12.9999, то строка вывода будет иметь вид:
Целое = 19951, Вещественное = 13.00
Можно сделать вывод, что целое число, несмотря на ограничения поля вывода 4 символами, выведется без изменений, а вещественное число будет округлено до сотых.
в) Знак минус используется для выравнивания числа влево внутри поля вывода.
printf ("Целое = %–4d, Вещественное = %–5.2f\n", my_int, my_float);
Если ввести значения 2 и 2.36666, то строка вывода будет иметь вид:
Целое = 2˽˽˽, Вещественное = 2.37˽
Если ввести значения -1999 и 12.9999, то строка вывода будет иметь вид:
Целое = –1999, Вещественное = 13.00
Пример использования форматированного ввода-вывода.
# include <stdio.h>
# define STR "Программа" // Для иллюстрации вывода строк.
void main (void)
{
|
|
|
// Вывод целого числа 336
printf ("%d\n", 336); // 336
printf ("%2d\n", 336); // 336, формат 2d игнорируется
printf ("%8d\n", 336); // ˽˽˽˽˽336 // ширина поля вывода = 8
printf ("%-8d\n", 336); // 336˽˽˽˽˽ // прижато влево ширина поля 8
printf("\n"); // Пропуск строки при выводе
// Вывод вещественного числа 12.345
printf ("%f\n", 12.345); // 12.345000
printf ("%e\n", 12.345); // 1.234500е+01
printf ("%10.1f\n", 12.345); // ˽˽˽˽˽˽12.3
printf ("%–12.1f\n", 12.345); // 12.3
printf("\n");
// Вывод строки символов по формату s
printf ("%s\n", STR); // Программа
printf ("%12s\n", STR); // ˽˽˽Программа
printf ("%12.5s\n", STR); // ˽˽˽˽˽˽˽Прогр
printf ("%-12.5s\n", STR); // Прогр
printf("\n");
}
Организация ввода/вывода в стиле С++
Для управления вводом/выводом данных в стиле С++ применяется заголовочный файл <iostream.h>. В нем определены стандартные объекты-потоки cin для ввода с клавиатуры и cout для вывода на экран, а также операции помещения в поток «и чтения из потока».
cin»список_ввода; // ввод значения данного с клавиатуры
cout«список_вывода; // вывода значения данного на экран
Пример программы, использующей функции ввода/вывода в стиле С:
# include <stdio.h>
int main()
{
int i;
printf("Введите целое число\n");
scanf("%d",&i);
printf("Вы ввели число %d, спасибо!",i);
return 0;
}
А вот как выглядит та же программа с использованием библиотеки классов C++:
# include <iostream.h>
int main()
{
int i;
cout«"Введите целое число\n";
cin»i;
cout«"Вы ввели число "«i«", спасибо!";
return 0;
}
Форматированный ввод/вывод в С++
Возможность управлять вводом-выводом в С++, обеспечивают форматирующие функции-члены, флаги и манипуляторы. Флаги, функции и манипуляторы выполняют одну и туже задачу – задают определённый формат ввода/вывода информации в потоках. Ввод/вывод на экран/с экрана в С++ осуществляется с помощью операторов cin и cout соответственно, а значит манипуляторы форматирования используются совместно с данными операторами ввода/вывода. Различие между функциями, флагами и манипуляторами форматирования состоит в способе их применения. Теперь рассмотрим способы применения объектов форматирования.
//Основные форматирующие функции-члены:
cout.fill('/*symbol*/'); // устанавливает символ заполнитель
//где symbol – символ-заполнитель, символ передаётся в одинарных кавычках
|
|
|
cout.width(/*width_field*/); // задает ширину поля
//где width_field - количество позиций (одна позиция вмещает один символ)
cout.precision(/*number*/); //задает количество знаков после десятичной
// точки, где number - количество знаков после десятичной точки
Доступ к функциям осуществляется через операцию точка, а в круглых скобках передаётся аргумент. Аргумент функции fill()может передаваться в виде символа, обрамленного одинарными кавычками или в виде числа (код символа). Одних функций не достаточно для форматирования потоков ввода/вывода, поэтому в С++ предусмотрен ещё один способ форматирования – флаги.
Флаги форматирования позволяют включить или выключить один из параметров ввода/вывода. Чтобы установить флаг ввода/вывода, необходимо вызвать функцию setf(), если необходимо отключить флаг вывода, то используется функция unsetf(). Далее показаны конструкции установки и снятия флагов вывода.
// установка флага вывода
cout.setf(ios::/*name_flag*/);
// где name_flag - это имя флага
Доступ к функциям оператора вывода выполняется через операцию точка. Метод setf()принимает один аргумент – имя флага. Флаги вывода объявлены в классе ios, поэтому, перед тем, как обратиться к флагу, необходимо написать имя класса – ios, после которого, с помощью операции разрешения области действия, вызвать нужный флаг.
// снятие флага вывода
cout.unsetf(ios::/*name_flag*/);
// где name_flag - это имя флага
Если при вводе/выводе необходимо установить/снять несколько флагов, то можно воспользоваться поразрядной логической операцией ИЛИ |. В этом случае конструкция языка C++ будет такой:
// установка нескольких флагов
cout.setf(ios::/*name_flag1*/ | ios::/*name_flag2*/ | ios::/*name_flag_n*/);
// снятие нескольких флагов
cout.unsetf(ios::/*name_flag1*/ | ios::/*name_flag2*/ | ios::/*name_flag_n*/);
В таблице 4 описаны некоторые основные флаги форматирования, а также показаны примеры их использования.
Таблица 4 – Некоторые флаги форматирования в С++
| Флаг | Назначение | Пример | Результат |
| cientific | Вывод чисел с плавающей точкой в экспоненциальной форме | cout.setf(ios::scientific); double value = 1024.165; cout << value << endl; | 1.024165e+003 |
| fixed | Вывод чисел с плавающей точкой в фиксированной форме (по умолчанию) | double value = 1024.165; cout << value << endl; | 1024.165 |
| right | Выравнивание по правой границе (по умолчанию). Сначала необходимо установить ширину поля (ширина поля должна быть заведомо большей чем, длинна выводимой строки). | cout.width(40); cout << «cppstudio.com» << endl; | __cppstudio.com |
| left | Выравнивание по левой границе. Сначала необходимо установить ширину поля(ширина поля должна быть заведомо большей чем, длинна выводимой строки). | cout.setf(ios::left); cout.width(40); cout << «cppstudio.com» << endl; | cppstudio.com__ |
Ещё один способ форматирования – форматирование с помощью манипуляторов. Манипулятор – объект особого типа, который управляет потоками ввода/вывода, для форматирования передаваемой в потоки информации. Отчасти манипуляторы дополняют функционал, для форматирования ввода/вывода. Но большинство манипуляторов выполняют точно, то же самое, что и функции с флагами форматирования. Есть случаи, когда проще пользоваться флагами или функциями форматирования, а иногда удобнее использовать манипуляторы форматирования. Именно по этому в С++ предусмотрено несколько средств форматирования ввода/вывода. В таблице 5 показаны основные манипуляторы форматирования С++.
|
|
|
Таблица 5 – Некоторые манипуляторы форматирования в С++
| Манипулятор | Назначение | Пример | Результат |
| endl | Переход на новую строку при выводе | cout << «website:» << endl << «cppstudio.com»; | website: cppstudio.com |
| scientific | Вывод чисел с плавающей точкой в экспоненциальной форме | double value = 1024.165; cout << scientific << value << endl; | 1.024165e+003 |
| fixed | Вывод чисел с плавающей точкой в фиксированной форме (по умолчанию). | double value = 1024.165; cout << fixed << value << endl; | 1024.165 |
| setw(int number) | Установить ширину поля, где number - количество позиций, символов (выравнивание по умолчанию по правой границе). Манипулятор с параметром. | cout << setw(40) << «cppstudio.com» << endl; | __cppstudio.com |
| right | Выравнивание по правой границе (по умолчанию). Сначала необходимо установить ширину поля(ширина поля должна быть заведомо большей чем, длинна выводимой строки). | cout << setw(40) << right << «cppstudio.com» << endl; | __cppstudio.com |
| left | Выравнивание по левой границе. Сначала необходимо установить ширину поля (ширина поля должна быть заведомо большей чем, длинна выводимой строки). | cout << setw(40) << left << «cppstudio.com» << endl; | cppstudio.com__ |
| setprecision(int count) | Задаёт количество знаков после запятой, где count - количество знаков после десятичной точки | cout << fixed << setprecision(3) << (13.5 / 2) << endl; | 6.750 |
| setfill(int symbol) | Установить символ заполнитель. Если ширина поля больше, чем выводимая величина, то свободные места поля будут наполняться символом symbol- символ заполнитель | cout << setfill(′0′) << setw(4) << 15 << ends << endl; |
При использовании манипуляторов необходимо подключить заголовочный файл <iomanip>
|
|
|
Лабораторная работа № 2
Программирование алгоритмов линейной структуры
ЦЕЛЬ РАБОТЫ: закрепление знаний о типах данных, преобразованиях типов, приобретение навыков составления и отладки программ линейной структуры на языке программирования C++
Выполнение работы: в соответствии с вариантом составить и реализовать программы.
Задание I
Написать программу для расчета по двум формулам. Предварительно подготовить тестовые примеры для второй формулы с помощью калькулятора (результаты вычисления по обеим формулам должны совпадать). Список стандартных математических функций C++ приведен в приложении 2. Отсутствующие в языке функции выразить через имеющиеся.
1.   . .
|
2.  
|
3.  
|
4.  
|
5.  
|
6.  
|
7.  
|
8.  
|
9.  
|
10.  
|
11.  
|
12.  
|
13.  
|
14.    . .
|
15.  
|
16.  
|
17.   (m > 0) (m > 0)
|
18.   (a > 0) (a > 0)
|
19. 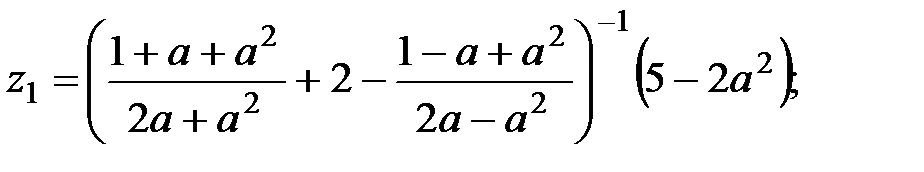 
|
20.  
|
21.   . .
|
22.   . .
|
23.   . .
|
24.    . .
|
25.   . .
|
Задание II
1. Составить программу вычисления объема конуса по заданному диаметру и образующей.
2. Дана сторона равностороннего треугольника. Составить программу нахождения площади этого треугольника и радиуса описанной окружности.
3. Известны радиусы двух концентрических окружностей. Составить программу нахождения площади кольца, образованного этими окружностями.
4. Составить программу нахождения суммы n членов арифметической прогрессии, для которой известен первый член, разность и число n.
5. Вычислить объем призмы, боковые грани которой - квадраты, а основанием служит равносторонний треугольник, вписанный в круг радиуса r.
6. Вычислить площадь прямоугольника, вписанного в окружность радиуса r, если отношение его сторон равно R.
7. Даны две стороны треугольника и угол между ними. Определить третью сторону и площадь.
8. Вычислить процент материала, ушедшего в отходы, если из куба с ребром а был выточен шар радиуса r (r < а).
9. Вычислить площадь кольца, ширина которого равна а, а отношение радиусов окружностей равно b.
10. Вычислить периметр и площадь прямоугольного треугольника, описанного около круга радиуса r, если гипотенуза треугольника равна с.
11. Вычислить диаметр трубы, пропускная способность которой позволяет заменить ею две трубы с диаметрами d 1 и d 2.
12. Вычислить высоты треугольника со сторонами a, b и с.
13. Вычислить площадь правильного n -угольника, описанного около круга радиусом r.
14. Высота конуса равна h, а радиус основания r. Вычислить объем шара, вписанного в конус.
15. Вычислить массу свинцовой трубы, длина которой равна b м (плотность свинца равна 11,4 г/см3), толщина стенок а мм, а внутренний диаметр трубы равен d мм.
16. Дан равносторонний треугольник. Вычислить сторону, высоту и площадь этого треугольника, если радиус вписанной окружности равен r.
17. Стальной вал, имеющий b мм длины и d мм в диаметре, обтачивается на токарном станке, при этом диаметр уменьшается при обточке на S мм. Вычислить, на сколько уменьшается масса тела (плотность стали 7,4 г/см3).
18. Вычислить объем призмы, боковые грани которой – квадраты. Основанием призмы служит равносторонний треугольник, заданный длиной стороны.
19. В конус с радиусом основания r и высотой h вписан цилиндр, радиус основания которого равен а. Вычислить объем цилиндра.
20. Даны две стороны треугольника d и с и угол между ними a. Найти радиусы окружностей: вписанной в треугольник и описанной около него.
21. Дана длина ребра куба. Найти объем куба и площадь его боковой поверхности.
22. Треугольник задан тремя сторонами. Вычислить его высоты.
23. Определить периметр правильного n -угольника, описанного около окружности радиуса R.
24. Смешано V 1 литров воды температуры Т 1 и V 2 литрами воды температуры Т 2. Найти объем и температуру образовавшейся смеси.
25. Известна длина окружности. Найти площадь круга, ограниченного этой окружностью.
26. Даны гипотенуза и катет прямоугольного треугольника. Найти второй катет и радиус вписанной окружности.
27. Найти площадь кольца, внутренний радиус которого равен R 1, а внешний - R 2 (R 2 > R l).
28. Определить время, через которое встретятся два тела, равноускоренно движущиеся навстречу друг к другу, если известны их начальные скорости, ускорение, начальное расстояние между ними.
29. Вычислить расстояние между двумя точками с координатами (x 1, y 1) и (x 2, y 2).
30. Даны катеты прямоугольного треугольника. Найти его гипотенузу и площадь.
Задание III
1. Радоновые ванны, применяемые для лечения, содержат 1.8·106 атомов радона в воде объемом 1.0 дм3. На сколько молекул воды приходится один атом радона в лечебной ванне?
2. Сколько атомов ртути содержится в воздухе объемом 1.0 м3 в помещении, зараженном ртутью, при температуре 20°С, если давление насыщенного пара ртути при этой температуре 133 мПа?
3. Какова длина ребра куба, содержащего 1.0·106 молекул идеального газа при нормальных условиях?
4. При какой температуре молекулы гелия имеют такую же среднюю скорость, как молекулы кислорода при 23°С?
5. Найдите среднюю кинетическую энергию поступательного движения молекул водорода, если при давлении 0.5 атм. их концентрация равна 1.5·109 м-3.
6. Газ нагревается в открытом сосуде при нормальном атмосферном давлении от 27°С до 327°С. Какое приращение получает при этом число молекул в единице объема газа?
7. В сосуде объемом 1 дм3 содержится некоторый газ при температуре 17°С. Найти приращение давления газа, если вследствие утечки газа из него выйдет 1021 молекул.
8. В сосуде объемом 3.0 дм3 находится гелий массой 4.0 мг, азот массой 70 мг и 5.0·1021 молекул водорода. Каково давление смеси, если температура ее 27°С?
9. Определить среднюю кинетическую энергию вращательного движения молекул водорода, содержащихся в 1.0 моль при 18°С.
10. При какой температуре молекулы кислорода имеют такую же среднюю скорость, как молекулы водорода при 25°С?
11. Сколько молекул содержится при нормальных условиях в 1м3 воздуха?
12. В сосуде объемом 2.0 дм3 находится газ под давлением 0.50 МПа. Чему равна средняя кинетическая энергия поступательного движения молекул газа?
13. Кислород массой 12 г находится при температуре 700°С, при этом 40% молекул диссоциировано на атомы. Чему равна средняя кинетическая энергия теплового движения частиц? Колебательные степени свободы молекул кислорода не возбуждаются.
14. Объём помещения 50 м3. температура воздуха зимой 0°С, а летом – 40°С. Какова разница в массе воздуха, заполняющего помещение зимой и летом? Принять μ = 29 кг/моль.
15. Плотность воздуха при нормальных условиях 1.3 г/л. Какова плотность воздуха при температуре 100°С и давлении 4.0·105 Н/м2?
16. Температура воздуха в баллоне объёмом 10 м3 при давлении 700 мм рт. ст. была 15°С. После нагрева воздуха до 20°С часть воздуха была вытеснена. Найдите массу вытесненного воздуха.
17. Сколько частиц (атомов и молекул) находится в азоте массой 1.0 г, если степень диссоциации азота 7.0%.
18. Какое давление на стенки сосуда производит кислород, если средняя квадратичная скорость его молекул 400 м/с и концентрация молекул 2.7·1019 м-3?
19. Найдите среднюю кинетическую энергию поступательного движения молекул гелия, если при давлении 0.5 атм. их концентрация равна 1.5·109 м3.
20. Определите температуру газа, если средняя кинетическая энергия поступательного движения его молекул равна 1.6·10-19 Дж.
21. Каково давление газа, если в каждом кубическом сантиметре его содержится 1.0·106 молекул, а температура газа 87°С?
22. Газ нагревается в открытом сосуде при нормальном атмосферном давлении от 22°С до 320°С. Какое приращение получает при этом число молекул в единице объема газа?
23. В сосуде объемом 15.0 дм3 находится газ под давлением 0.50 МПа. Чему равна средняя кинетическая энергия поступательного движения молекул газа?
24. При какой температуре молекулы гелия имеют такую же среднюю скорость, как молекулы водорода при 27°С?
25. Газ занимает объём 2 л при давлении 5·105 Н/м2. Определите суммарную энергию поступательного движения молекул газа.
Задания для самостоятельной работы
1. Даны два действительных числа. Найти среднее арифметическое и среднее геометрическое этих чисел.
2. Даны четыре целых числа. Найти среднее арифметическое этих чисел и среднее геометрическое этих чисел.
3. Треугольник задан длинами своих сторон. Используя формулу Герона, найти площадь этого треугольника.
4. Идет k -я секунда суток. Определить сколько полных часов H, полных минут М прошло к этому моменту.
5. Даны два момента времени одних суток: H 1, H 2 - часы, M 1, M 2 - минуты. Определить интервал между этими моментами в часах H и минутах M.
6. По трем координатам вершин некоторого треугольника найти его высоту.
7. Найти объем и площадь боковой поверхности конуса радиусом r, высотой h и образующей l.
8. Вычислить боковую поверхность пирамиды (пирамида правильная, усеченная), если известны р и p 1 - полупериметры нижнего и верхнего оснований и k - апофема.
9. Найти объем и полную поверхность полого шара, если известны r 1 и r 2 - радиусы внешней и внутренней шаровых поверхностей.
10. Вычислить площадь поверхности и объем усеченного конуса высотой h, радиусами r 1 и r 2, образующей l.
11. В шар радиуса r вписан конус с углом а при вершине в осевом сечении конуса. Определить объем и полную поверхность конуса.
12. Вычислить объем цилиндра, вписанного в правильную шестиугольную призму, у которой каждое ребро равно а.
13. Найти площадь равнобокой трапеции с основаниями А и В и углом a при большем основании A.
14. Треугольник задан величинами своих углов и радиусом описанной окружности. Найти, стороны треугольника.
15. Найти объем правильной треугольной пирамиды, если стороны ее основания равны а и плоский угол при ее вершине равен a.
16. Вычислить радиус шара, вписанного в правильную четырехугольную пирамиду, если стороны основания пирамиды равны а и двухгранный угол при основании равен a.
|
|
|


