 |
алгоритмизация и программирование 8 глава
|
|
|
|
- static – статическая переменная. Время жизни – постоянное. Инициализируется один раз при первом выполнении оператора, содержащего определение переменной. В зависимости от расположения оператора описания статические переменные могут быть глобальными и локальными. Глобальные статические переменные видны только в том модуле, в котором они описаны.
- register – аналогично auto, но память выделяется по возможности в регистрах процессора. Если такой возможности у компилятора нет, переменные обрабатываются как auto.
int a; // 1 глобальная переменная а
int main()
{
int b; // 2 локальная переменная b
extern int x; // 3 переменная х определена в другом месте
static int c; // 4 локальная статическая переменная с
a = 1; // 5 присваивание глобальной переменной
int a; // 6 локальная переменная а
a = a; // 7 присваивание локальной переменной
::a = 3; // 8 присваивание глобальной переменной
return 0;
}
int x = 4; // 9 определение и инициализация х
В этом примере глобальная переменная а определена вне блоков. Память под нее выделяется в сегменте данных в начале работы программы, областью действия является вся программа. Область видимости – вся программа, кроме строк 6-8, так как в первой из них определяется локальная переменная с тем же именем, область действия начинается с точки ее описания и заканчивается при выходе из блока. Переменные b и c – локальные, область их видимости – блок, но время жизни различно: память под b выделяется в стеке при входе в блок и освобождается при выходе из него, а переменная с располагается в сегменте данных и существует все время, пока работает программа.
Если при определении начальное значение переменных явным образом не задается, компилятор присваивает глобальным и статическим переменным нулевое значение соответствующего типа. Автоматические переменные не инициализируются.
|
|
|
Имя переменной должно быть уникальным в своей области действия (например, в одном блоке не может быть двух переменных с одинаковыми именами).
Для определения области действия идентификаторов надо придерживаться правил:
- каждый идентификатор должен быть описан перед тем, как будет использован;
- областью действия идентификатора является блок, в котором он описан;
- все идентификаторы в блоке должны быть уникальными, т.е. не повторяться;
- один и тот же идентификатор может быть по-разному определен в каждом отдельном блоке.
Если идентификатор пользовательской функции совпадает с именем стандартной функции, то последняя недоступна в области действия функции, объявленной пользователем, т.е. стандартная функция игнорируется, а выполняется функция пользователя.
5.4. Функции
Под функцией понимается совокупность операторов, совместно выполняющих некоторое действие, имеющее определенную цель, оформленная в соответствии с требованиями языка программирования.
С понятием функции в языке C++ связано три следующих компонента:
- описание функции;
- прототип;
- вызов функции.
Описание функции состоит из двух частей: заголовка и тела. Описание функции имеет следующую форму записи:
тип_результата имя_функции ([список_параметров]) // заголовок
{
/* объявления и операторы
или, другими словами, тело функции*/
}
Здесь тип_результата – тип возвращаемого значения. В случае отсутствия спецификатора типа предполагается, что функция возвращает целое значение (int).Если функция не возвращает никакого значения, то на месте типа записывается спецификатор void. В списке параметров для каждого параметра должен быть указан тип. При отсутствии параметров список может быть пустым или иметь спецификатор void.
Тело функции представляет собой последовательность объявлений и операторов, описывающих определенный алгоритм. Важным оператором тела функции является оператор возврата в точку вызова: return [выражение];. Оператор return имеет двойное назначение. Он обеспечивает немедленный возврат в вызывающую функцию и может использоваться для передачи вычисленного значения функции. В теле функции может быть несколько операторов return, но может не быть и ни одного. В последнем случае возврат в вызывающую программу происходит после выполнения последнего оператора тела функции.
|
|
|
Прототип функции может указываться до вызова функции вместо описания функции для того, чтобы компилятор мог выполнить проверку соответствия типов аргументов и параметров. Прототип функции по форме такой же, как и заголовок функции, в конце его ставится «;». Параметры функции в прототипе могут иметь имена, но компилятору они не нужны.
Компилятор использует прототип функции для сравнения типов аргументов с типами параметров. Язык Cи не предусматривает автоматического преобразования типов в случаях, когда аргументы не совпадают по типам с соответствующими им параметрами, т. е. язык Cи обеспечивает строгий контроль типов. При наличии прототипа вызываемые функции не обязаны размещаться в одном файле с вызывающей функцией. То есть, описание тел функций можно разместить в другом файле, который необходимо подключить к исходному с использованием директивы #include.
Вызов функции может быть оформлен в виде оператора, если у функции отсутствует возвращаемое значение, или в виде выражения, если существует возвращаемое значение.
В первом случае оператор имеет следующий формат:
имя_функции ([список_аргументов]);
Например: Print(“Hello World!”);
Во втором случае выражение записывается следующим образом:
Переменная = имя_функции (список_аргументов);
Например: z = max(x, y);
Значение вычисленного выражения является возвращаемым значением функции. Возвращаемое значение передается в место вызова функции и является результатом ее работы.
Число и типы фактических параметров (аргументов) должны совпадать с числом и типом формальных параметров (параметров) функции. При вызове функции фактические параметры (аргументы) подставляются вместо формальных параметров (параметров). Таким образом, описание функции задает формальную схему обработки информации, в то время как оператор вызова функции осуществляет настройку этой формальной схемы на конкретную обработку фактических данных.
|
|
|
Ниже приводится пример функции с возвращаемым значением.
Пример 1. Составить программу, содержащую обращение к функции вычисления максимума из двух чисел.
Возможное решение данной задачи имеет вид:
//описание функции max находится в данном файле ниже тела главной функции
# include <conio.h>
# include <iostream>
using namespace std;
// описание пользовательской функции
int max (int a, int b) // заголовок функции
{
int с; //
c=(a>b)?a:b; // тело функции
return с; //
}
void main()
{
setlocale(LC_ALL,"Rus");
int x,y,z;
cout << "\n поочередно введите х и у \n";
cin >> х >> y;
z = max (х, y); // вызов функции
cout << "z=" << z;
return;
}
Описание функции находится в одном файле с главной программой.
Вызов функции является выражением в правой части оператора присваивания z = max(x,y);, при выполнении которого значения аргументов х и у подставляются вместо параметров а и bсоответственно (передача параметров в функцию по значению). После выполнения тела функции возвращаемое значение передается в место вызова функции и присваивается переменной z.
В рассмотренной программе функция имеет возвращаемое значение. Существуют задачи, которые не требуют передачи возвращаемого значения. Такой пример приведен ниже.
Пример 2. Использование функции без возвращаемого значения.
Составить программу, включающую в свой состав функцию, при обращении к которой обеспечивается выдача на экран символа, набранного на клавиатуре. При нажатии клавиши Enter выполнение программы завершить.
...
void print(char); // прототип функции
void main()
{
char x;
cout <<”\nВводите символы.”<<” Enter – окончание ввода”;
do
{
x = getch();
print (x);
}
while (x! == 13);
return 0;
}
void print(char a) { cout <<a << “\t“; }
В функции print() отсутствует возвращаемое значение, поэтому обращение к функции осуществляется оператором вызова функции print(x);. В результате обращения к функции на экран будет выведен символ, введенный с клавиатуры с помощью оператора x = getch().
|
|
|
Лабораторная работа №5
Использование функций для решения прикладных задач
ЦЕЛЬ РАБОТЫ: закрепление теоретических знаний и приобретение навыков программирования функций.
Выполнение работы: освоить теоретический материал, выполнить общее для всех задание I и в соответствии с вариантом составить программу (задание II), реализовав пользовательскую функцию.
Задание I
Изучить порядок объявления и описания функций:
- реализовать (отладить и запустить программы) приведенные в теоретических сведениях примеры 1 – 2;
- оформить в тетради, записав условие, блок-схему и результат работы соответствующих программ (примеры 1 – 2).
Задание II
В соответствии с вариантом составить и реализовать программу:
1. Три прямоугольных треугольника заданы катетами. Определить, площадь какого из них больше.
2. Три отрезка заданы координатами вершин. Определить, есть ли среди них отрезки равной длины.
3. В порт в среднем приходит три корабля в день. Какова вероятность того, что в порт придёт 2 корабля? 4 корабля? Вычисление вероятности производится по формуле: Р = 3k e-3/ k!.
4. Найти среднее арифметическое действительных корней трёх квадратных уравнений.
5. Даны три различных бруска, имеющих форму кубов с заданным произвольным ребром. Из каждого выпилена правильная четырехугольная пирамида (основание – грань куба). Вычислить объем материала, ушедшего в отходы.
6. Даны действительные числа а и b. Вычислите,
g (l.2, a)+ g (b, a)- g (2 a - 1, ab), где 
7. Заданы длины рёбер произвольной треугольной пирамиды. Вычислить площадь полной поверхности этой пирамиды.
8. Вычислить объем «снеговика», состоящего из трех шаров с произвольными радиусами.
9. Каждое из трех колец задано внутренним и внешним радиусами. Чему равна площадь наибольшего кольца?
10. Вычислить значение выражения a! + b! + c! + d!.
11. Вычислить площадь «елки», состоящей из четырех треугольников с известными сторонами.
12. Найти минимальное значение среди корней трех квадратных уравнений (каждое уравнений задано тройкой коэффициентов).
13. Даны действительные числа a и b. Вычислить
max (u + v 2, 3.14),
где u = max(a, b), v = max(ab, a + b), а max – подпрограмма для вычисления максимального значения для двух данных чисел.
14. Даны радиусы трех шаров. Вычислить среднее арифметическое объемов этих шаров.
15. Дана арифметическая прогрессия an ,, a 1 – первый ее элемент, d – разность. Найти второй, третий, четвертый и седьмой элементы и их сумму.
16. Даны действительные числа s и t. Вычислить f (t, -2 s, 1.17) + f (2.2, t, s - t),
.
17. Найти наибольшее из пяти заданных чисел, используя подпрограмму нахождения наибольшего из двух чисел.
|
|
|
18. Вычислить значение функции:
, если 
19. Вычислить значение функций
и 
для значений х = 0,1; 0,35; 0,53.
20. Вычислить значение функции x = 2 f (15) - 4 f (-1) g (11) + g (32), если
f (x) = 10 x + e2 x; 
.
21. Из куба со стороной а выпилили куб со сторой b (a > b). Какой процент материала ушёл в отходы?
22. Каждая из трёх окружностей задана координатами центра и координатами точки на окружности. Какова наибольшая длина окружности?
23. Найти наименьшее из четырёх заданных чисел, используя подпрограмму нахождения наименьшего из двух чисел.
24. Даны действительные числа a и b. Вычислить
min (2 u - v 2, 4.5),
где u = min(a, b), v = min(a/b, a - b), а min – подпрограмма для вычисления минимального значения для двух данных чисел.
25. Вычислить большие вещественные корни квадратных уравнений а х 2 + b х + с = 0 и t х 2 + p х + q = 0, если они существуют. В противном случае вывести на экран монитора соответствующее сообщение.
Контрольные вопросы
1. Что такое подпрограмма?
2. Как подпрограмму можно реализовать в С++?
3. Какие параметры называются формальными?
4. Какие параметры называются фактическими?
5. Что такое переменная?
6. Что такое область действия идентификатора?
7. Что такое локальная переменная? Что такое глобальная переменная?
8. Какова область действия локальных идентификаторов?
9. Какова область действия глобальных идентификаторов?
10. Что такое функция?
11. Чем отличается объявление функции от ее определения?
12. Перечислите составные части описания функции.
13. Что такое прототип функции?
14. Как описывается функция пользователя в программе?
15. Что такое возвращаемое значение функции?
16. Как осуществляется вызов функций из основной программы?
Пример выполнения лабораторной работы
Задание. Задавая с клавиатуры координаты вершин треугольника, определить, является ли он равносторонним.
Решение
1. Математическая модель
Треугольник является равносторонним, если длины его сторон равны. Находим длины сторон треугольника, используя подпрограмму нахождения расстояния между двумя точками.
Аргументы: a1, b1, c1, a2, b2, c2 целого типа – координаты вершин треугольника.
Результаты: текстовое сообщение.
Промежуточные величины: АВ, ВС, АС вещественного типа – длины сторон треугольника.
Расстояние между двумя точками А(х1,у1) и В(х2,у2) находим по формуле:
АВ = sqrt(sqr(x2 - x1) + sqr(y2 - y1).
2. Алгоритм – основная программа: – подпрограмма:
| АВ = dlina (a1,b1,a2,b2) |
| ВС = dlina (b1,c1, b2,c2) |
| АС = dlina (a1,c1,a2,c2) |
| да |
| нет |
| конец |
| начало |
| a1,a2,b1,b2,c1,c2 |
| (АВ=ВС)&&(BC=AC) &&(AB=AC) 0and |
| является |
| не является |
| dlina(х1,у1,х2,у2) |
| конец |
| АВ=sqrt(sqr(x2-x1) + sqr(y2-y1) |
3. Программа 4. Результат работы программы:
#include <iostream>
#include <conio.h> Задайте координаты точек А, В, С
#include <math.h> 0 0 6 6 5 1
const double eps = 0.01;
using namespace std; Треугольник не является равносторонним
double Dlina (double x1,double y1,double x2,double y2) {
return (sqrt((x1-y1)*(x1-y1)+(x2-y2)*(x2-y2)));
}
int main(){
cout<<endl<<"Задайте координаты точек А, В, С"<<endl;
double a1, a2, b1, b2, c1, c2;
cin>>a1>>a2>>b1>>b2>>c1>>c2;
double ab, bc, ac;
ab = Dlina(a1, b1, a2, b2);
bc = Dlina(b1, c1, b2, c2);
ac = Dlina(a1, c1, a2, c2);
if((fabs(ac-bc)<eps) && (fabs(bc-ab)<eps) && (fabs(ac-ab)<eps))
cout<<endl<<"Треугольник является равносторонним";
else cout<<endl<<"Треугольник не является равносторонним";
_getch();
return 0;
}
6. Итерация и рекурсия
6.1. Понятие итеративного процесса
Итеративный процесс можно определить как процесс вычислений, основанный на повторении последовательности операций, при котором на каждом шаге повторения используется результат предыдущего шага. Примерами итеративных алгоритмов могут служить алгоритмы вычисления факториала натурального числа, последовательности чисел Фибоначчи, вычисление суммы членов последовательности с заданным числом слагаемых и т.д. Итеративные процессы программируются обычно с помощью циклических конструкций.
Пример. Вычисление факториала числа n.
int factor (int n)
{
int f = 1;
for (int i = 2; i <= n; i++) f *= i;
return k;
}
6.2. Понятие рекурсии
В то же время повторение последовательности действий можно осуществить и другим методом, основанным на принципе возможности явного включения в конструкции языка программирования конструкции того же вида. В частности, в языке программирования C++ всякая функция может вызывать сама себя. Такой вызов называется рекурсией. Функция, вызывающая саму себя, называется рекурсивной.
Вообще алгоритм решения задачи называется рекурсивным, если он выражается в терминах решения более простой версии той же задачи и, кроме того, в нем предусмотрено решение самого простого варианта задачи.
При рекурсивном вызове функций в С++ используется стековая организация хранения локальных параметров.
Стек является простейшей динамической структурой организации данных. Добавление элементов в стек и выборка из него выполняются из одного конца, называемого вершиной стека. Говорят, что стек реализует принцип обслуживания LIFO (last in — first out, последним пришел - первым ушел (обслужен)).
Стеки широко применяются в системном программном обеспечении, компиляторах, в различных рекурсивных алгоритмах.
Различия между итерацией и рекурсией:
1) итерации необходим цикл и вспомогательные величины, в то время как рекурсия обходится без вспомогательных величин и обычно проще для понимания, короче и нагляднее итерации;
2) итерация требует меньше места в оперативной памяти именьших затрат машинного времени, чем рекурсия, которой необходимы затраты на управление стеком;
3) при реализации рекурсии велика вероятность переполнения стека.
Поэтому при выборе способа описания функции следует вначале решить, чему отдать предпочтение – эффективности программы или ее компактности. Однако следует избегать рекурсий там, где есть очевидное итерационное решение. Вместе с тем существует много хороших примеров применения рекурсии (построение графических образов разнообразных узоров, работа с двоичными деревьями).
При рекурсивном описании функции последняя всегда должна содержать, по крайней мере, одну альтернативную нерекурсивную ветвь алгоритма с условием окончания вычислений, заканчивающуюся оператором возврата результата.
Различают две формы рекурсивных подпрограмм:
- прямая рекурсия;
- косвенная рекурсия.
В первом случае функция содержит вызов этой же функции.
Косвенная рекурсия возникает в том случае, когда две или более функций вызывают друг друга. В случае двух функций: некоторая функция обращается к другой функции, а та в свою очередь вызывает первоначальную функцию. Для предотвращения зацикливания одна или обе функции должны проверять условие завершения.
Пример: Составить рекурсивную функцию, вычисляющую факториал числа n по формуле (учесть, что 0! = 1):
long fact (long n)
{
if (n==0 || n == 1) return 1;
return (n*fact(n-l));
}
То же самое можно записать короче:
long fact (long n)
{
return (n > 1)? n*fact(n-l): 1;
}
Пример: Распечатать последовательность, состоящую из n букв А и n букв В.
void abn (int n)
{
cout<<”A”;
if (n > 1) abn(n-l);
cout<<”B”;
Return
}
Лабораторная работа №6
Программирование рекурсивных алгоритмов
ЦЕЛЬ РАБОТЫ: закрепление навыков программирования с использованием рекурсивных функций.
Выполнение работы: в соответствии с вариантом, используя прямую рекурсию,составить и реализовать программу.
Задание
1. Описать рекурсивную функцию NOD(A, B) целого типа, находящую наибольший общий делитель (НОД) двух целых положительных чисел A и B, используя алгоритм Евклида: НОД(A, B) = НОД(B, A mod B), если B ≠ 0; НОД(A, 0) = A. С помощью этой функции найти НОД(A, B), НОД(A, C), НОД(A, D), если даны числа A, B, C, D.
2. Для n = 12 найти числа Фибоначчи. Числа Фибоначчи: F(0) = 1, F(1) = 1 F(n) = F(n - 2) + F(n - l)
3. Даны целые числа m и n, где 0 ≤ m ≤ n, вычислить, используя рекурсию, число сочетаний С(n, m) по формуле: 
, 
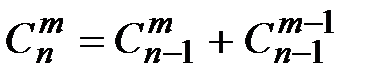при 0 ≤ m ≤ n. Воспользовавшись формулой 
можно проверить правильность результата.
4. Опишите рекурсивную функцию, которая по заданным вещественному х и целому п вычисляет величину хn согласно формуле:
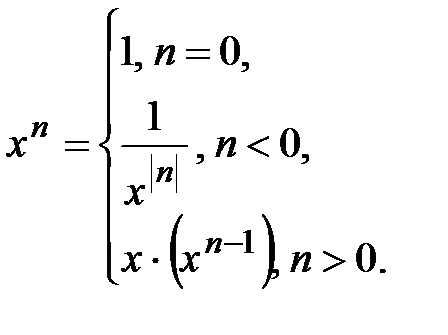
5. Задана последовательность положительных чисел, признаком конца которых служит отрицательное число. Используя рекурсию, подсчитать количество чисел и их сумму.
6. Напишите рекурсивную функцию K (n), которая возвращает количество цифр в заданном натуральном числе n, используя формулу:
7. Определим функцию S (n), вычисляющую сумму цифр заданного натурального числа:
Описать рекурсивную функцию DigitSum(K) целого типа, которая находит сумму цифр целого числа K, не используя оператор цикла. С помощью этой функции найти суммы цифр для пяти данных целых чисел.
8. Дан вектор X из n вещественных чисел. Найти минимальный элемент вектора, используя вспомогательную рекурсивную функцию, находящую минимум среди элементов вектора X, начиная с n -гo.
9. Напишите рекурсивную функцию для нахождения биномиальных коэффициентов (для заданного М ≥ i ≥ j > 0 вычислите все 
):
10. Напишите программу вычисления функции Аккермана для всех неотрицательных целых аргументов т и п:
11. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:
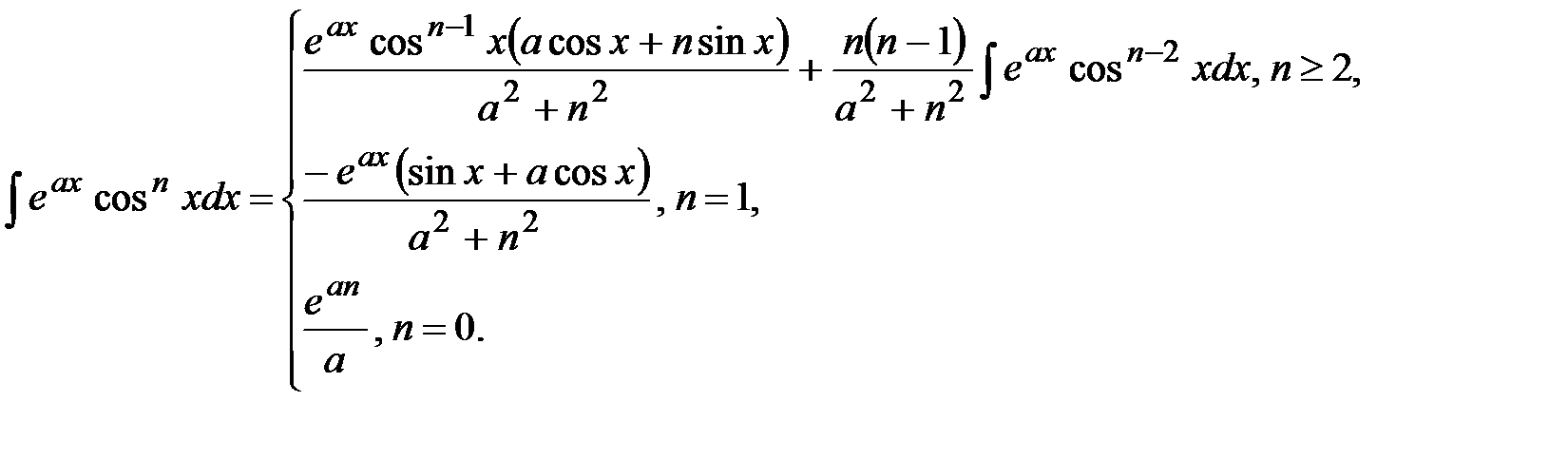
12. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:
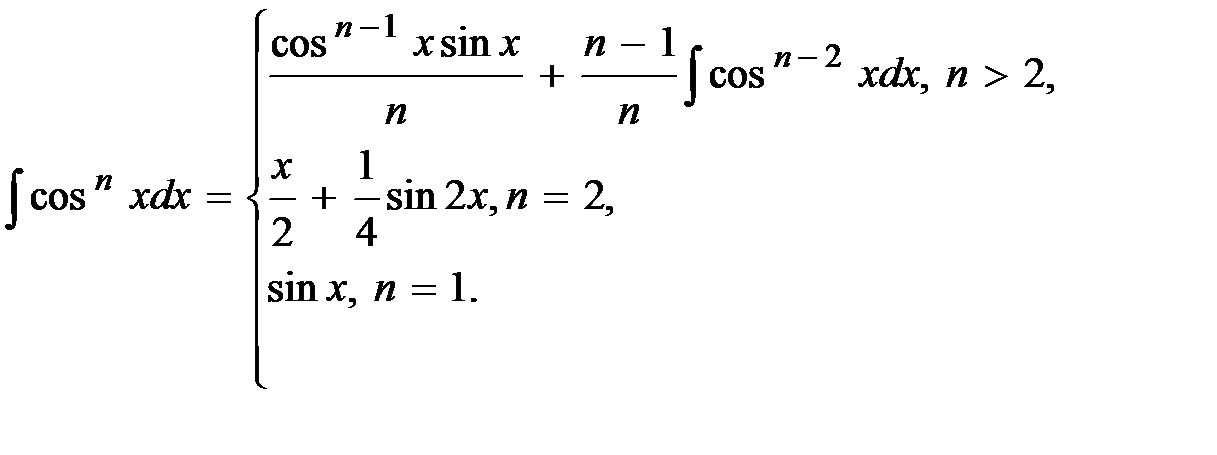
13. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:
14. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:
15. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:
16. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:
17. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:
18. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:
19. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:
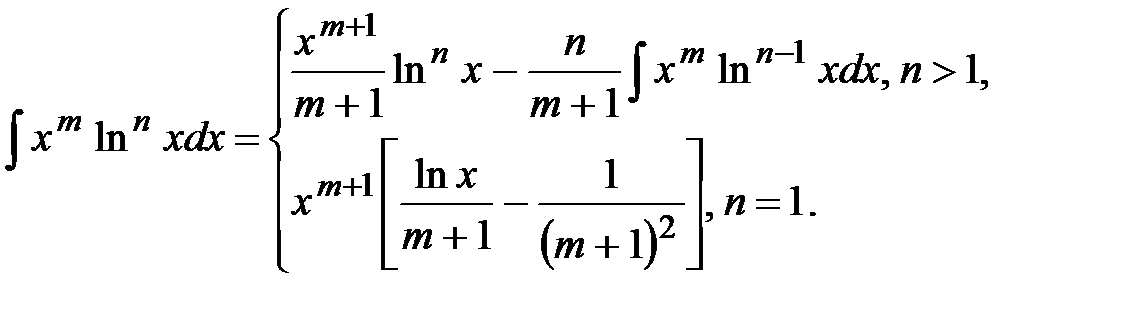
20. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:
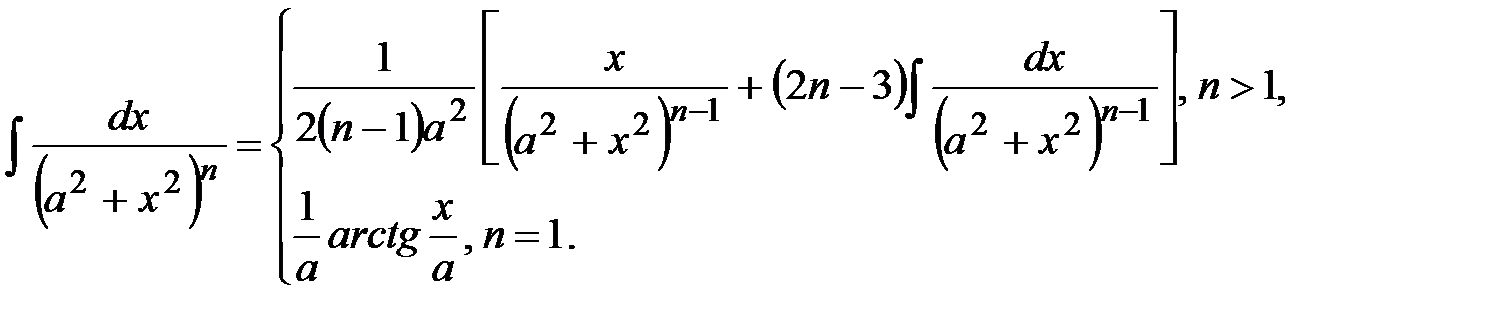
21. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:
22. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:
23. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:
24. Для заданных границ интегрирования а и b вычислите значение определенного интеграла следующего вида:
25. Напишите рекурсивную функцию, перемножающую два целых числа, одно из которых неотрицательно, без использования операции умножения.
Контрольные вопросы
1. Какой процесс называется итеративным?
|
|
|
