алгоритмизация и программирование 11 глава

≤ ≤ … ≤ ( ≥ ≥ … ≥ )

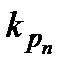Сортировка называется устойчивой, если она удовлетворяет дополнительномуусловию: записи с одинаковыми ключами остаются в прежнем порядке, т.е. p_i < p_j, если и i < j.

Так как каждый ключ идентифицирует соответствующую запись, то эти записи можнои не определять при сортировке, рассматривая лишь их ключи (в простейшемслучае, когда запись состоит лишь из сортируемых элементов, понятия записи и ключ совпадают).

При внутреннейсортировке выбранный метод должен экономно использовать время работыпроцессора и память. Хорошие алгоритмы затрачивают на сортировку n записей время порядка n log n, а мерой эффективности можетслужить число необходимых сравнений ключей и число перестановок записей. Эти числа являются функциями от n – числа сортируемых записей.

При сортировке массивов будем предполагать, что перестановки, переводящие элементы массива в нужный порядок, должны выполняться на том же месте, т.е. без использования промежуточного массива. Методы, в которых элементы из массива A передаются в результирующий массив В, представляют значительно меньший интерес.

9.6. Прямые и быстрые методы внутренней сортировки

Все методы внутренней сортировки делятся на прямые и быстрые (или улучшенные) [7].

Для прямых методов сортировки требуется порядка n ² сравнений ключей, они более просты и удобны для объяснения характерных черт основных принципов большинства сортировок. Программы этих методов легко понимать и они короче программ быстрых алгоритмов.

Улучшенные методы сортировки требуют небольшого числа операций, но эти операции обычно сами более сложны, и поэтому для достаточно малых n прямые методы оказываются быстрее, хотя при больших значениях n их использовать не следует.

Методы внутренней сортировки можно разбить в соответствии с определяющими их принципами на три класса:

1. Сортировка вставками: элементы просматриваются по одному, и каждый новый элемент вставляется на подходящую позицию среди ране упорядоченных элементов.

2. Сортировка с помощью выбора: сначала выделяется наименьший (или наибольший) элемент и каким-либо образом отделяется от остальных, затем выбирается наименьший (наибольший) из оставшихся элементов и т.д.

3. Сортировка с помощью обмена: последовательно просматриваются пары соседних элементов; если элементы в паре образуют инверсию (т.е. неупорядочены), то они меняются местами.

Все прямые методы сортировки фактически передвигают каждый элемент массива на каждом элементарном шаге на одну позицию. Поэтому требуют O (n ²) таких шагов. В основу любых улучшенных методов положен принцип перемещения элементов на каждом шаге сортировки на большие расстояния. Такой подход позволяет существенно уменьшить время сортировки, но усложнить алгоритмы выполнения.

Улучшенный метод обмена – Шейкерная сортировка, метод Хоара (самый быстрый из известных на сегодняшний день методов внутренней сортировки),

усовершенствование сортировки прямого включения – метод Шелла,

прямого выбора – сортировка с помощью бинарного дерева.

9.7. Сортировка вставками

Рассмотрим процесс сортировки методом вставки (прямого включения) массива а[1], а[2],..., a[n]. Вначале в исходном массиве выделяется уже отсортированная, например по неубыванию, часть а[1] ≤ а[2] ≤...≤ а[i-1] и не отсортированная a[i], a[i+l],..., a[n]. Затем с шагом 1, начиная с i = 2 чередуя сравнения и перемещения элемента a[i], в отсортированной части массива определяется такой индекс (ключ) j (1 ≤ j ≤ i -1), чтобы выполнялись неравенства a[j-l] ≤ a[i] ≤ a[j]. Если такой индекс найден, то элемент a[i] вставляется на соответствующее место. Для этого выполняется сдвиг на одну позицию вправо элементов отсортированной части: a[j], …, а[i-1]. После этого осуществляется переход к следующему значению i. В противном случае просто происходит переход к следующему значению i. С каждым шагомотсортированная часть массива увеличивается на один элемент. Очевидно, что для выполнения полной сортировки потребуется n -1 шаг, где n - число элементов исходного массива.

Покажем процесс сортировки вставками на примере целочисленного массива а[1..12], состоящего из чисел 22, -14, 13, 28, 6, 41, -5, 18, 0, 35, 6,-15 (значком * обозначены вставленные элементы, выделены элементы отсортированной части)

Исходный массив:		-14					-5					-15
1-й шаг	-14*						-5					-15
2-й шаг:	-14	13*					-5					-15
3-й шаг:	-14	13		28*			-5					-15
4-й шаг:	-14	6*					-5					-15
5-й шаг:	-14	6				41*	-5					-15
6-й шаг:	-14	-5*	6				41					-15
7-й шаг:	-14	-5			18*							-15
8-й шаг:	-14	-5	0*			18						-15
9-й шаг:	-14	-5	0			18			35*			-15
10-й шаг:	-14	-5			6*		18					-15
11-й шаг:	-15*	-14	-5

Как видно из примера, в процессе сортировки на первом шаге первый элемент исходного массива считается отсортированным, а следующий за ним элемент сравнивается с ним. Если этот элемент больше, он остается на своем месте, в противном случае первый элемент сдвигается на вторую позицию, а второй помещается на первую (как в нашем примере). Далее все выбираемые элементы из неотсортированной части массива последовательно сравниваются с элементами отсортированной части, начиная с первого, до тех пор, пока не встретится больший или равный ему. Этот элемент и все последующие элементы отсортированной части перемещаются на одну позицию вправо (или вниз, если массив расположен в столбик), освобождая место для нового элемента. Этот процесс закончится при выполнении одного из двух условий:

· найден первый слева элемент a[j] ≥ a[i], что говорит о необходимости вставки a[i] между a[j] и a[j-1], в частности, если j=1, то a[i] помещается в первую позицию, что влечет за собой необходимость увеличения диапазона индекса массива на единицу;

· достигнут правый конец отсортированной части массива (правый барьер), следовательно, элемент a[i] нужно оставить на прежнем месте.

Заметим, что сравнение и перемещение элемента a[i] в отсортированной части массива можно проводить и справа налево, начиная с (i-1)-го элемента.

9.8. Сортировка с помощью прямого выбора

Сортировка массива размером n в неубывающем (невозрастающем) порядке методом прямого выбора выполняется по следующему алгоритму.

1. Выбирается элемент данного массива с минимальным (максимальным) значением (или ключом).

2. Выбранный элемент и первый элемент меняются местами.

3. Этот процесс повторяется с оставшимися n - 1 элементами, затем с n - 2 элементами и т.д. до тех пор, пока не останется один, самый большой/меньший элемент.

Всего потребуется n - 1 раз выполнить указанную последовательность действий. В процессе сортировки будет увеличиваться отсортированная часть массива, а неотсортированная соответственно уменьшаться.

В отличие от сортировки вставками, когда а каждом шаге рассматривается только один очередной элемент исходного массива и все элементы отсортированной части, среди которых ищется место для вставки, при прямом выборе для поиска одного элемента с наименьшим (наибольшим) ключом просматриваются все элементы исходного массива и найденный элемент помещается как очередной в отсортированную часть массива.

Напомним, что во всех рассматриваемых методах сортировки мы не используем промежуточных массивов.

Схему сортировки методом прямого выбора проиллюстрируем на примере массива, рассмотренного в предыдущем пункте. Элементы, которые меняются местами на очередном шаге, выделены полужирны шрифтом, а минимальные элементы неотсортированной части, кроме того, отмечены звездочкой. Отсортированная часть подчеркнута.

Исходный массив:		-14					-5					-15*
1-й шаг	-15	-14*					-5
2-й шаг:	-15	-14					-5*
3-й шаг:	-15	-14	-5						0*
4-й шаг:	-15	-14	-5		6*
5-й шаг:	-15	-14	-5								6*
6-й шаг:	-15	-14	-5				13*
7-й шаг:	-15	-14	-5					18*
8-й шаг:	-15	-14	-5									22*
9-й шаг:	-15	-14	-5									28*
10-й шаг:	-15	-14	-5									35
11-й шаг:	-15	-14	-5

9.9. Сортировка с помощью прямого обмена

Алгоритм данного метода сортировки заключается в последовательных просмотрах массива от начала к концу и обмене местами соседних элементов, если они образуют инверсию. Опишем алгоритм сортировки по неубыванию подробнее.

Пусть задан массив a размером n. Начинаем просмотр массива с первой пары элементов a[1] и a[2]. Если первый элемент этой пары больше второго, то меняем их местами, иначе оставляем их без изменения и сравниваем вторую пару элементов а[2] и а[3]. Если а|2] > а[3], то меняем их местами и т.д. На первом шаге будут просмотрены все пары элементов массива: а[i] и а[i+1] для i от 1 до n -1. В результате такого просмотра и необходимых обменов максимальный элемент переместится в конец массива и будет являться отсортированной частью. На втором шаге аналогичная процедура проводится с первого до (n - 1)-гo элемента. Тем самым второй по величине элемент массива переместится на предпоследнее место. Отсортированная часть будет содержать два элемента. Эти действия продолжаются до тех пор, пока количество элементов в неотсортированной части массива не уменьшится до двух.Нaпоследнем шаге выполняется упорядочение оставшихся двух элементов. После (n - 1) шагов массив окажется отсортированным по неубыванию. Для иллюстрации отсортируем массив по неубыванию методом простого обмена. Отсортированная часть выделена полужирным шрифтом.

 

Исходный массив:		-14					-5					-15
1-й шаг	-14					-5					-15
2-й шаг:	-14				-5					-15
3-й шаг:	-14			-5					-15
4-й шаг:	-14		-5					-15
5-й шаг:	-14	-5					-15
6-й шаг:	-14	-5				-15
7-й шаг:	-14	-5			-15
8-й шаг:	-14	-5		-15
9-й шаг:	-14	-5	-15
10-й шаг:	-14	-15	-5
11-й шаг:	-15	-14	-5

Сортировку методом прямого обмена называют еще методом "пузырька" Это название происходит от образной интерпретации, при которойэлементы данного массива расположены вертикально и в процессе выполнения сортировки на каждом шаге более легкие элементы, как пузырьки в ванне с водой, поднимаются до уровня, соответствующего их весу.

Лабораторная работа № 9
Задачи сортировки и поиска

ЦЕЛЬ РАБОТЫ: Закрепление теоретических знаний и приобретение практических навыков по составлению алгоритмов и программ различных методов сортировки.

Выполнение работы: в соответствии с заданиями пунктов 1-4, учитывая вариант (п. 3), составить и реализовать программу.

Задание

1. Сформировать при помощи генератора псевдослучайных чисел линейный целочисленный массив A[20], таким образом, что бы элементы массива принадлежали отрезку [-50, 50].

2. Выполнить в нём линейный поиск заданного элемента.

3. Отсортировать массив определённым методом в соответствии с вариантом (см. таблицу).

Метод сортировки	Вариант
Вставкой	1, 4, 7, 10, 13, 16, 19, 22
Обменом	2, 5, 8, 11, 14, 17, 20, 23
Выбором	3, 6, 9, 12, 15, 18, 21, 25

4. Выполнить бинарный поиск элемента.

Формирование массива, вывод его на экран, линейный поиск, сортировку и бинарный поиск оформить в виде соответствующих функций.

 

Контрольные вопросы

1. Понятие сложности алгоритмов.

2. На какие классы делятся алгоритмы в соответствии с их временной или пространственной сложностью?

3. Постановка задачи сортировки данных.

4. Прямые и быстрые методы внутренней сортировки.

5. Алгоритм сортировки массива методом вставки.

6. Алгоритм сортировки массива методом прямого выбора.

7. Алгоритм сортировки массива методом прямого обмена.

8. Понятие инверсии.

9. Постановка задачи поиска элемента в массиве.

10. Алгоритм последовательного (линейного) поиска.

11. Алгоритм бинарного поиска.

10. Указатели и массивы

10.1. Понятие статической и динамической переменной

Ранее были рассмотрены простые и структурированные типы данных, которые определяются в начале программы или подпрограммы и их структура остается неизменной в течение всей работы программы. Компилятор после анализа раздела переменных отводит каждой переменной соответствующее число ячеек и закрепляет их на все время работы блока. Размер выделяемого места зависит от типа переменной. Такие переменные создаются при входе в блок и прекращают свое существование, когда вычислительный процесс выходит из блока. Они не меняют своих размеров и называются статическими.

Однако существует класс задач, в которых память должна выделяться динамически, в процессе решения. Наиболее часто встречаются списки с заранее неизвестным числом объектов. Для таких задач используются динамические переменные. Они хранятся в некоторой области памяти, не обозначенные идентификатором, а со ссылкой на эту область. Такой вид доступа позволяет динамически занимать и освобождать память в процессе работы программы (блока). Динамические переменные образуются при помощи ссылочного типа данных. При образовании динамической переменной создается значение ссылочного типа – адрес места памяти, где находится вновь созданная переменная.

10.2. Указатели

Указатель – это переменная, значение которой равно значению адреса памяти, по которому лежит значение некоторой другой переменной. В этом смысле имя этой другой переменной отсылает к ее значению прямо, а указатель - косвенно. Ссылка на значение посредством указателя называется косвенной адресацией.

Указатели, подобно любым другим переменным, перед своим использованием должны быть объявлены. Объявление указателя имеет вид:

type *ptr;

где type - один из предопределенных или определенных пользователем типов, а ptr - указатель. Например,

int *countPtr, count;

объявляет переменную countPtr типа int* (т.е. указатель на целое число) и переменную count целого типа. Символ * в объявлении относится только к countPtr. Каждая переменная, объявляемая как указатель, должна иметь перед собой знак «звездочка» (*). Если в приведенном примере желательно, чтобы и переменная count была указателем, надо записать:

int *countPtr, *count;

Символ * в этих записях обозначает операцию косвенной адресации.

Может быть объявлен и указатель на void:

void *Pv;

Это универсальный указатель на любой тип данных. Но прежде, чем его использовать, ему надо в процессе работы присвоить значение указателя на какой-то конкретный тип данных. Например:

Pv = countPtr;

В Cи указатели используются широко. Они должны инициализироваться либо при своем объявлении, либо с помощью оператора присваивания. Указатель может получить в качестве начального значения 0, NULL или адрес. Указатель с начальным значением 0 или NULL ни на что не указывает. NULL – это символическая константа, определенная с целью показать, что данный указатель ни на что не указывает. Пример объявления указателя с его инициализацией:

int *countPtr = NULL;

Для присваивания указателю адреса некоторой переменной используется операция адресации &, которая возвращает адрес своего операнда. Например, если имеются объявления

int Step = 5;

int *ptr, Num;

то оператор

ptr = &Step;

присваивает адрес переменной Step указателю ptr.

Для того чтобы получить значение, на которое указывает указатель, используется операция *, обычно называемая операцией косвенной адресации или операцией разыменования. Она возвращает значение объекта, на который указывает ее операнд (т.е. указатель). Например, если продолжить приведенный выше пример, то оператор

Num = *ptr;

присвоит переменной Num значение 5, т.е. значение переменной Step, на которую указывает ptr.

Операцию разыменования нельзя применять к указателю на void, поскольку для него неизвестно, какой размер памяти надо разыменовывать.

Здесь необходимо обратить внимание на разночтение символа «*». Если символ «*»стоит перед идентификатором переменной при ее объявлении, то смысл этой «звездочки» – сказать, что объявляется не обычная переменная, а переменная-указатель. Во всех остальных случаях символ «*» читается и воспринимается программой как «взятие значения по адресу», то есть является операцией косвенной адресации.

10.3. Взаимосвязь между массивами и указателями

Массивы и указатели в Си тесно связаны и могут быть использованы почти эквивалентно. Имя массива можно понимать как константный указатель на первый элемент массива. Его отличие от обычного указателя только в том, что его нельзя модифицировать. Например, задан целочисленный массив A, состоящий из 5 элементов:

int A[5]={-2,5,4,-17,3};

Посмотрим, как этот массив разместится в оперативной памяти (рис. 10.1).

	...
A[4]	-17 -2 0x0012FF80
	0x0012FF90
A[3]		0x0012FF8C
A[2]		0x0012FF88
A[1]		0x0012FF84
A[0]		0x0012FF80
	...
const int *A		0х0012FF70
	...

Рисунок 10.1 – Представление массива элементов в памяти ЭВМ

Стоит обратить внимание на то, что под хранение значения каждого элемента массива выделяется четыре 8 битных ячейки памяти. На рисунке 10.1 справа видна последовательность адресов ячеек памяти, содержащая значения, различающиеся на четыре байта. Это связано с тем, что тип элементов данного массива – int. Причем, под хранение адреса начала массива выделяется тоже четыре байта, так как все указатели для 32-разрядных процессоров 4-х байтные.

Указатели можно использовать для выполнения любой операции, включая индексирование массива. Допустим, сделано следующее объявление:

int b[5] = {1,2,3,4,5}, *Pt;

Здесь объявлены массив целых чисел b[5] и указатель на целое Pt. Поскольку имя массива является указателем на первый элемент массива, то можно задать указателю Pt адрес первого элемента массива b с помощью оператора Pt = b;

Это эквивалентно присваиванию адреса первого элемента массива следующим образом: Pt = &b[0];

Теперь можно сослаться на элемент массива b[3] с помощью выражения *(Pt + 3).

Указатели можно индексировать точно так же, как и массивы. Например, выражение Pt[3] ссылается на элемент массива b[3].

Или, например, определение int a[5];задает массив из пяти элементов а[0], a[1], a[2], a[3], a[4]. Если объект *у определен как

int *у; то оператор у = &a[0];

присваивает переменной у адрес элемента а[0]. Если переменная у указывает на очередной элемент массива а, то y+1 указывает на следующий элемент, причем здесь выполняется соответствующее масштабирование для приращения адреса с учетом длины объекта (для типа int – 4 байта, long – 4 байта, double – 8 байт и т.д.). Так как само имя массива есть адрес его нулевого элемента, то оператор у = &a[0]; можно записать и в другом виде: у = а. Тогда элемент а[1] можно представить как *(а+1). С другой стороны, если у – указатель на массив a, то следующие две записи: a[i] и *(у+i) эквивалентны. Рассмотрим пример:

int main()

{

int a[5]={-5,0,34,12,-17};

cout<<endl<<(a+2); // оператор 1

cout<<endl<<&a[2]; // оператор 2

cout<<endl<<*(a+2); // оператор 3

cout<<endl<<a[2]; // оператор 4

cout<<endl;

return 0;

}

Так, операторы 1 и 2 выведут одно и то же значение – адрес элемента массива с индексом 2. А операторы 3 и 4 – одно и то же значение 34.

Между именем массива и соответствующим указателем есть одно важное различие. Указатель – это переменная и у = а или y++ – допустимые операции. Имя же массива – константа, поэтому конструкции вида a = y, a++ использовать нельзя, так как значение константы постоянно и не может быть изменено.

Указатели могут применяться как операнды в арифметических выражениях, выражениях присваивания и выражениях сравнения. Однако, не все операции, обычно используемые в этих выражениях, разрешены применительно к переменным указателям.

С указателями может выполняться ограниченное количество арифметических операций. Указатель можно увеличивать (++), уменьшать (--), складывать с указателем целые числа (+ или +=), вычитать из него целые числа (- или -=) или вычитать один указатель из другого.

⇐ Предыдущая6789101112131415Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: