 |
Расчет реакции линейной цепи на входное воздействие произвольного вида с применением временных характеристик цепи
|
|
|
|
Переходные процессы в цепях с двумя разнородными реактивными элементами
Временные характеристики цепей
Расчет реакции линейной цепи на входное воздействие произвольного вида с применением временных характеристик цепи
Список используемых источников
1. Возникновение переходных процессов и законы коммутации
Для изучения темы реферата необходимо знать расчет установившихся режимов, т.е. таких, когда все токи и напряжения либо постоянные, либо периодически повторяющиеся функции времени, но в любой схеме могут происходить подключения и отключения ветвей (происходит коммутация). Обозначают коммутацию: 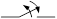 . В линейных цепях коммутация считается идеальной, т.е.:
. В линейных цепях коммутация считается идеальной, т.е.:
1) ключ представляет собой либо разрыв, либо провод;
2) длительность перехода из одного состояния в другое равна нулю. Момент времени сразу после коммутации обозначают  либо
либо  , а момент времени непосредственно перед коммутацией соответственно обозначают
, а момент времени непосредственно перед коммутацией соответственно обозначают 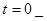 ,
,  . После коммутации цепь стремится под действием источников схемы прийти к новому установившемуся режиму, но для этого ей требуется время. Процессы, происходящие в цепи после коммутации, называются переходными процессами.
. После коммутации цепь стремится под действием источников схемы прийти к новому установившемуся режиму, но для этого ей требуется время. Процессы, происходящие в цепи после коммутации, называются переходными процессами.
Почему этот переход не может произойти мгновенно? Дело в том, что в цепи имеются элементы L и C, в которых запасается определенная величина энергии WL=L  2/2 и WC=Cu2/2 соответственно. В новом установившемся режиме будет другой запас энергии, и, т.к. скорость изменения энергии есть подводимая к элементу мощность, получается, что требуется конечное время на изменение этого запаса энергии (т.к. источников бесконечной мощности в реальной цепи нет). Из выражения для WL и WC и того факта, что в цепях не развивается бесконечная мощность, вытекают два фундаментальных условия, без которых невозможно рассчитать ни один переходной процесс – это законы коммутации.
2/2 и WC=Cu2/2 соответственно. В новом установившемся режиме будет другой запас энергии, и, т.к. скорость изменения энергии есть подводимая к элементу мощность, получается, что требуется конечное время на изменение этого запаса энергии (т.к. источников бесконечной мощности в реальной цепи нет). Из выражения для WL и WC и того факта, что в цепях не развивается бесконечная мощность, вытекают два фундаментальных условия, без которых невозможно рассчитать ни один переходной процесс – это законы коммутации.
|
|
|
Получим их:
 ,
,
т.к. P  , L - конечное число,
, L - конечное число,  L - конечное число, то
L - конечное число, то  - скачка быть не может. Отсюда вытекает один из законов коммутации: ток в индуктивности не может измениться скачком, поэтому при коммутации:
- скачка быть не может. Отсюда вытекает один из законов коммутации: ток в индуктивности не может измениться скачком, поэтому при коммутации:  . Дифференцируя dWC/dt, приходим ко 2-ому закону коммутации: напряжение на ёмкости не может измениться скачком, поэтому при коммутации:
. Дифференцируя dWC/dt, приходим ко 2-ому закону коммутации: напряжение на ёмкости не может измениться скачком, поэтому при коммутации: 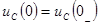 . Т.к.
. Т.к. 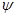 = L
= L  L,
L,  , то можно использовать и такие функции:
, то можно использовать и такие функции: 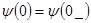 ,
,  .
.
Про остальные величины, в том числе и про скорость изменения любых токов и напряжений при коммутации заранее ничего не известно и их приходится рассчитывать. Т.к. и форма изменения токов и напряжений неизвестна, приходится использовать самые общие выражения: 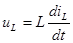 ,
,  . Тогда уравнения, описывающие цепь после коммутации, оказываются дифференциальными. В линейной цепи – это линейные дифференциальные уравнения (ЛДУ). Существуют различные методы решения таких уравнений, и соответственно различают различные методы расчета переходных процессов.
. Тогда уравнения, описывающие цепь после коммутации, оказываются дифференциальными. В линейной цепи – это линейные дифференциальные уравнения (ЛДУ). Существуют различные методы решения таких уравнений, и соответственно различают различные методы расчета переходных процессов.
2 Способы получение характеристического уравнения
Классический метод
Классический метод основан на решении ЛДУ методом вариации произвольных постоянных. Любая система ЛДУ может быть сведена к одному уравнению n –ого порядка. В цепях по схеме после коммутации порядок определяется так: n = n L + n C – nОК – nОС , где n L – число L; n C – число C; nОК – число особых контуров, т.е. таких, которые состоят только из емкостей и источников ЭДС; nОС – число особых сечений (в простейшем случае, это узлы схемы, к которым подключены только ветви с источником тока или с индуктивностями).
Решение уравнения представляют в виде суммы частного решения неоднородного уравнения (ЛНДУ) и общего решения линейного однородного дифференциального уравнения (ЛОДУ). Частное решение определяется видом правой части уравнения. В цепях в правой части уравнения стоят источники энергии схемы после коммутации. Физический смысл частного решения уравнения в цепях – это новый установившийся режим, к которому будет стремиться схема после коммутации под действием источников. Поэтому частное решение ЛНДУ называют принужденной составляющей режима. Общее решение ЛОДУ физического смысла не имеет. В противоположность принужденной составляющей, его называют свободной составляющей переходного процесса. Свободная составляющая записывается в виде суммы слагаемых, число и вид которых определяются корнями характеристического уравнения.
|
|
|
После записи решения необходимо рассчитать произвольные постоянные, вошедшие в выражение общего решения. Это можно сделать, если известны начальные условия. Начальные условия – это значения искомой функции времени и необходимого числа её производных по времени в начале переходного процесса, т.е. при t=0.
Все начальные условия делят на две группы:
- независимые начальные условия, это  L(0) и uC(0), которые находятся по законам коммутации, с помощью вычисленных ранее
L(0) и uC(0), которые находятся по законам коммутации, с помощью вычисленных ранее  L(0-) и uC(0-) в схеме до коммутации;
L(0-) и uC(0-) в схеме до коммутации;
- все остальные начальные условия – зависимые. Их приходится искать из цепи после коммутации в переходном режиме по законам Кирхгофа для мгновенных значений токов и напряжений при t=0 с помощью независимых начальных условий. Имея необходимое число начальных условий и рассматривая решение и его производные по времени в момент  , получают систему линейных алгебраических уравнений (СЛАУ) из которой находят произвольные постоянные.
, получают систему линейных алгебраических уравнений (СЛАУ) из которой находят произвольные постоянные.
В соответствии с изложенным, порядок расчета переходного процесса классическим методом может быть таким:
1) рассматривают установившийся режим схемы до коммутации и находят  L(0-) и uC (0-);
L(0-) и uC (0-);
2) рассматривают цепь после коммутации в новом установившемся режиме и находят принужденную составляющую переходного процесса;
3) тем или иным способом получают характеристическое уравнение и находят его корни в соответствии с которыми определяют вид свободной составляющей;
4) записывают решение в виде суммы принужденной и свободной составляющих.Если характеристическое уравнение n – ого порядка, то формируется система линейных алгебраических уравнений (СЛАУ) n - ого порядка, включающая (n-1) производную решения. Переписывают СЛАУ для  ;
;
|
|
|
5) рассматривают цепь после коммутации в переходном режиме; рассчитывают необходимые начальные условия (ННУ);
6) подставляют ННУ в СЛАУ при  и находят произвольные постоянные;
и находят произвольные постоянные;
7) записывают полученное решение.
Способы получения характеристического уравнения
Существуют различные способы получения характеристического уравнения.
Если цепь описывается всего одним уравнением, то его алгебраизируют: d/dt заменяют на p,  dt заменяют на 1/p, правую часть обращают в ноль и получают характеристическое уравнение.
dt заменяют на 1/p, правую часть обращают в ноль и получают характеристическое уравнение.




Если режим в цепи описывается системой из нескольких уравнений, то методом подстановки их сводят к одному и поступают точно также как описано выше (обычно так не делает).
Универсальный способ
Систему уравнений по законам Кирхгофа для цепи после коммутации алгебраизируют и составляют определитель системы, и приравняв его к нулю, получают характеристическое уравнение.
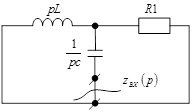
Воспользуемся этим способом.
Пусть схема после коммутации имеет вид:

 ,,
,,
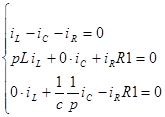

Если в схеме нет управляемых источников и взаимных индуктивностей, то проще всего поступить так: в схеме после коммутации все источники заменить их внутренним сопротивлением, вместо индуктивности L написать pL, вместо емкости C написать  .
.
а) Если в полученной схеме нет ветви без сопротивления, томожно разомкнуть любую ветвь полученной пассивной схемы и относительно точек разрыва записать выражение для нахождения  .
.
б) Если в полученной схеме есть ветви без сопротивления, то размыкать надо именно ту ветвь, в которой ищется переходный ток или напряжение и относительно точек разрыва записывают  .
.
Характеристическое уравнение имеет вид:
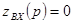 .
.
Для рассмотренного выше примера получим:

Выражение для свободной составляющей содержит столько слагаемых, сколько есть корней, а слагаемые имеют такой вид:
|
|
|
а) каждому простому вещественному корню  соответствует слагаемое
соответствует слагаемое  .
.
Если два корня, то процесс апериодический.
б) двум комплексно-сопряженным корням:  и
и  соответствует A1ePx1 t +A2ePx2 t, где A1, A2 – получаются комплексными числами, причем комплексно-сопряженными числами. Поэтому с помощью формулы Эйлера этот результат можно записать в другом виде (где не будет j):
соответствует A1ePx1 t +A2ePx2 t, где A1, A2 – получаются комплексными числами, причем комплексно-сопряженными числами. Поэтому с помощью формулы Эйлера этот результат можно записать в другом виде (где не будет j):  .
.
По этому выражению не очень удобно строить графики. Используя формулы тригонометрии его можно преобразовать (либо в sin, либо в cos): Ce-  t sin(
t sin( ct+
ct+  1)=De-
1)=De-  t cos(
t cos( c t+
c t+  2) – затухающий во времени гармонический процесс – колебательный процесс.
2) – затухающий во времени гармонический процесс – колебательный процесс.
в) среди корней есть m одинаковы[ (если таких корней два, то переходный процесс называется критическим).

 ;
;

Пример: Дано: E=40В, R1 =R2=400 Ом, L=5Гн, C=5 мкФ. Найти  .
.
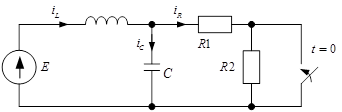
1) В схеме до коммутации стоит постоянный источник, следовательно, ток в установившемся режиме постоянный.
t<0
 ,
,  .
.
Если источник ЭДС синусоидальный, то эту часть задачи решают символическим методом.
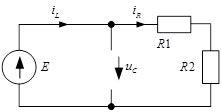
2) Рассчитывают новый установившийся режим, находят принужденную составляющую.
t 
Видно, что после коммутации в схеме есть только постоянный источник ЭДС и поэтому в принужденном режиме – постоянный ток.

 .
.
3) получают характеристическое уравнение
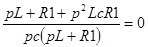

 .
.
4) записывают решение
5) определяют начальные условия
Для схемы после коммутации записывают систему уравнений по законам Кирхгофа. Число этих уравнений больше, чем число неизвестных, однако при t=0, известны все iL(0) и uC(0), поэтому при добавлении этих независимых условий из полученной при t=0 системы можно найти все остальные зависимые начальные условия, например, методом подстановки.
При решении надо выразить значения токов и напряжений в момент t=0, их производные по времени в момент t=0 через параметры элементов схемы и независимые начальные условия.
Например, для нашей задачи:


В нашей задаче для расчета 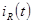 надо найти 2 начальных условия, т.к. имеем 2 корня характеристического уравнения и 2 произвольные постоянные, поэтому надо знать
надо найти 2 начальных условия, т.к. имеем 2 корня характеристического уравнения и 2 произвольные постоянные, поэтому надо знать  R(0) и
R(0) и 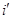 R(0).
R(0).
Из (1):
 ,
,
Из (3):


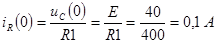 ,
,
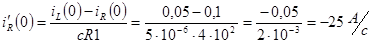 .
.
6) расчет произвольных постоянных
В нашем случае:


При  :
:
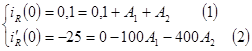
Тогда из (1) 
Из (3)  (2)
(2) 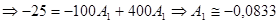
Ответ:  , А.
, А.
3. Особенности переходных процессов в цепях с одним реактивным элементом
В таких цепях характеристическое уравнение будет первого порядка. Получить это уравнение можно, например, так:
По способу Zвх(p)=0, при этом схемы могут иметь вид:

Рис (1) 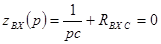 ,
,  ,
,
Рис (2) 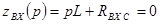 ,
, 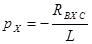 .
.
Видно, что корень характеристического уравнения получается отрицательным, т.е. с течением времени свободная составляющая  .
.
|
|
|
Ясно, что в разных схемах различными получаются величина А, величина  , но свободная составляющая всегда будет иметь вид затухающей экспоненты. Для таких функций вводятся специальная характеристика.
, но свободная составляющая всегда будет иметь вид затухающей экспоненты. Для таких функций вводятся специальная характеристика.
Постоянная времени цепи (τ) – есть интервал времени, за который амплитуда свободной составляющей уменьшается в e раз.
Воспользовавшись этим определением, можно найти τ таким образом так как 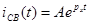 , то
, то
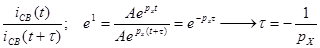 .
.
В цепи:  ,
, 
т.е. τ зависит только от параметров рассматриваемой цепи (τ не зависит от начальных условий и напряжений источника).
Используя понятие τ, можно условно ввести понятие длительности переходного процесса. Так как  , то
, то
| t | τ | 3τ | 5τ |

| 0,36 | 0,05 | 0,004 |
В соответствие с этой таблицей принимают, что переходный процесс длится  . К концу этого времени график переходного процесса практически сливается с принужденной составляющей.
. К концу этого времени график переходного процесса практически сливается с принужденной составляющей.
Если известен график переходного процесса, из него можно найти τ.
Проще всего сделать так: на глаз определить, где кончается переходный процесс.
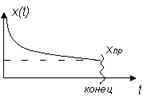
Длительность переходного процесса делят на 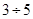 . Это и будет τ.
. Это и будет τ.
- Из графика переходного процесса вычитают принужденную составляющую. Это будет график свободной составляющей. Задаются моментом времени t1 и находят из графика xсв(t1). Делят эту величину на e и получают xсв(t1+ τ). Находят на графике эту величину, из нее определяют время t2 и затем находят τ как τ = t2 - t1

- τ есть величина под касательной к графику переходного процесса. Подкасательная – это проекция на ось времени от точки, в которой проведена касательная до точки пересечения этой касательной с асимптотой.

Пример: Дано: 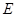 ,
,  ,
,  . Найти i(t), uc(t)
. Найти i(t), uc(t)

1) t<0
i(0_)=0, uc(0_)=0,
2) t→∞
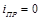 ,
,  ,
,
Должен существовать переходной процесс, в течении которого от источника энергия передается к конденсатору, а по проводам идет ток, заряжающий конденсатор.

3) 

 ,
,
4)  ;
;  ,
,
 ,
,
 ,
, 

 ,
, 
5) Расчет начальных условий.



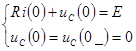
Тогда из  получают
получают 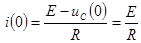
6) 
 ,
, 

Пример: Дано: 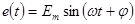 ,
,  ,
,  . Найти
. Найти  .
.
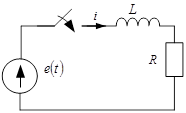
1) 
 ,
,  ,
, 
2) Расчет принужденной составляющей.
В данном случае принужденный режим есть синусоидальный ток, поэтому расчет проведем символическим методом.
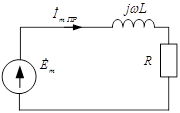
 ,
, 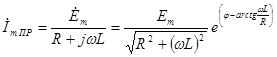
Переходят к мгновенному значению:
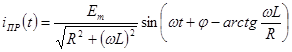 ,
,
3)  ;
;  ,
, 
4) 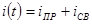
5) 
6)  ,
,

7) 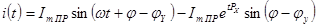
 ,
, 
График проще всего построить по этапам:
1) принужденная составляющая;
2) exp соответствует свободной составляющей суммы этих графиков.
|
|
|


