 |
Расчет реакции линейной цепи на входное воздействие произвольного вида с применением временных характеристик цепи
|
|
|
|
Раньше мы рассматривали два вида входного воздействия:
1) xвх= δ(t)-на входе будет импульсная характеристика g(t);
2) xвх= 1(t)-переходная характеристика h(t).
При произвольном заданном виде входного воздействия, в линейной цепи тоже можно найти реакцию. Для этого годятся и g(t) и h(t) и передаточная функция H(p), но в зависимости от формы входного сигнала, сложности цепи и того математического аппарата, которым располагаешь, более удобно будет применить какую-то одну из этих характеристик.
Рассмотрим применение переходной характеристики h(t):
1) На входе действуют прямоугольным импульсом

Воспользуемся принципом наложения и представим этот импульс в виде двух скачков Um1(t) и -Um1(t-tu).
Если нам известна переходная характеристика на h(t), то реакция на каждый скачок записывается очень просто Umh(t) и -Umh(t-tu) (h(t)=1-e-t/τ).
Вся реакция определяется сложением этих двух графиков.
Т.е. для 0≤t<tu Uвых(t)=Umh(t), t≥tu Uвых(t)=Umh(t)–Umh(t-tu).
2) Входной сигнал – функция, которая в некоторые моменты времени изменяется скачком, а между этими моментами постоянно.

И в этом случае задача решается просто: раскладываем входной сигнал на совокупность скачков и записываем для каждого интервала времени свое выражение для реакции:
0≤t<10-3 xвых=5∙h(t)
10-3≤t<2∙10-3 xвых=5∙h(t)+10∙h(t-10-3)
t≥2∙10-3 xвых=5∙h(t)+10∙h(t -10-3) -18∙h(t -2∙10-3).
Все такие задачи решаются с помощью h(t).
1) Входной сигнал в некоторый момент времени имеет скачки, а между
этими моментами времени плавно изменяется по тому-то закону (или вообще плавно изменяется без скачков).

Представим себе, что этот сложный сигнал приближенно м.б. составлен из нескольких скачкообразных воздействий (первое воздействие имеет амплитуду xвх(0) и возникает в момент t=0, второе воздействие возникает в некоторый момент t1 и имеет амплитуду xвх(t1)-xвх(0)=∆xвх(t1), третий сигнал поступает в момент t2 и имеет амплитуду ∆xвх(t2) и т.д.). Значит можно написать, что для некоторого момента t:
|
|
|
xвх(t)≈xвх(0)1(t)+∑∆xвх(tj)1(t-tj) (*).
В сумме учитывая все те ступеньки, которые возникли до нашего момента времени t. Если ступеньки брать помельче, выражение будет получаться поточнее, но все равно приближенно. Получим теперь точное выражение. В нашем случае:
xвых(t)≈xвх(0)h(t)+∑∆xвх(tj)∙h(t-tj) (**).
Известно, что ∆xвх(tj)/∆tj≈x(tj) и тогда (**) перепишется xвых(t)≈xвх(0)∙h(t)+∑xвх′(tj)∆tjh(t-tj). Уменьшая ∆tj до dtj вместо суммы получим интеграл: (для удобства записи tj→λ)
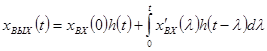
Если бы функция имела скачки не только в момент 0, но и в какие-то другие моменты. Пришлось бы для каждого интервала времени в котором функция непрерывна, записывать свои выражения отличающиеся друг от друга наличием реакции на скачки случившиеся до рассмотрения момента времени t.
Пример: Есть h(t)=0,5e-500t. Надо найти реакцию цепи на входное воздействие.

Описывает входное воздействие аналитически. В нашем случае можно считать, что в интервале от 0 до 10-3 Uвх1(t)=a+b∙t:
30=10+b∙10-3; a=10; b=2∙104.
Uвх2(t)=15+A∙e-t/τ ; τ=8∙10-4 ; t/τ=10-3/8∙10-4 ;
Uвх2(t=10-3)=5=15+A∙e-1,25; A≈-30.
Теперь для каждого интервала времени записываем свое выражение:
0≤t<10-3


 .
.
Берем интеграл, приводим подобные члены, строим графики. Но в рамках курса ТОЭ РГРТУ требуется ответ до состояния
t≥10-3


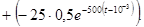
Применение импульсных характеристик
Известно, что
1) g(t)=  -1{H(p)},
-1{H(p)},
2) xвых(p)=xвх(p)H(p),
3) 
 =
=  ,
,
Пусть  ,
,  ,
,
тогда  =
=  -1
-1  =
= 
Фактически это есть другая форма интеграла Дюамеля, которая может быть получена используя связь g(t) и h(t). Порядок применения получения выражения такой же, но при численном нахождении интеграла удобней использовать собственно интеграл Дюамеля.
|
|
|
Применение передаточной функции
Если известно H(p) и xвх(t), можно записать изображение xвх(p), вычислить xвых(p)=H(p)xвх(p) и перейти к оригиналу.
Особенно удобно применять H(p)тогда, когда xвх(t) имеет простой вид, позволяющий легко записать изображение xвх(p) либо сразу для всего сигнала, либо разложение его на более простые компоненты и воспользовавшись принципом положения.
Например:
xвх(t)=10e-100t


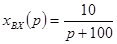 ,
,  ,
,
 ,
,  ,
,  ,
,
 ,
,  ,
,
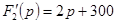 ,
,
 ,
,


Этот входной сигнал можно представить в виде совокупности двух более простых. Тогда
1) Для 0 ≤t<10-2
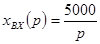 ,
,
2) Для t≥10-2, t<2∙10-2

3)  .
.
Теперь умножая на H(p) находим изображающие реакции и затем переходим к оригиналу.
Список используемых источников
1. Основы теории цепей. Учебник для вузов./ Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов.-5-е изд. перераб.-М.: Энергоатомиздат, 1989. 528 с.
2. В.П. Попов. Основы теории цепей. Учебник для вузов. -М.: Высшая школа, 1985. 496 с.
3. Теория электрических цепей: Методические указания к лабораторным работам / Рязан. гос. радиотехн. акад.; Сост.: С.М. Милюков, В.П. Рынин; Под ред. В.П. Рынина. Рязань, 2002. 16 с.,2004. 20 с. (№3282, №3624)
4. Электротехника и электроника: Методические указания к расчетно-графической работе / Рязан. гос. радиотехн. акад.; Сост. Г.В. Спивакова. Рязань, 2005. 16 с. (№3665)
5. М.Р. Шебес. Теория линейных электрических цепей в упражнениях и задачах. М.: Высшая школа, 1990. 528 с.
6. Матханов П.Н. Основы анализа электрических цепей. Нелинейные цепи: Учеб. для электротехн. спец. вузов. –2-е изд., перераб. и доп. –М.: Высш. шк., 1986. –352 с.
7. Каплянский А.Е. и др. Теоретические основы электротехники. Изд. 2-е. Учеб. пособие для электротехнических и энергетических специальностей вузов. –М.: Высш. шк., 1972. -448 с.
8. Теоретические основы электротехники. Т. 1. Основы теории линейных цепей. Под ред. П.А. Ионкина. Учебник для электротехн. вузов. Изд. 2-е, перераб. и доп. –М.: Высш. шк., 1976. –544 с.
|
|
|


