 |
Обоснование цены товара фирмы-монополиста
|
|
|
|
Рассматривается фирма, производящая однородную продукцию с квадратичной функцией затрат 
 положительные постоянные,
положительные постоянные,  выпуск продукции). Так как запасы продукции не предусматриваются и отсутствуют конкуренты, выпуск
выпуск продукции). Так как запасы продукции не предусматриваются и отсутствуют конкуренты, выпуск  всегда устанавливается равным спросу. Спрос предполагается зависящим не только от цены
всегда устанавливается равным спросу. Спрос предполагается зависящим не только от цены  но также от скорости
но также от скорости  ее изменения:
ее изменения: 
 Таким образом, прибыль фирмы является функцией двух переменных
Таким образом, прибыль фирмы является функцией двух переменных  :
:

Целью фирмы является нахождение оптимальной функции, максимизирующей общую прибыль  на конечном промежутке времени
на конечном промежутке времени  Этот промежуток предполагается достаточно коротким, чтобы функции спроса и затрат можно было считать фиксированными. Следовательно, задача состоит в отыскании функции
Этот промежуток предполагается достаточно коротким, чтобы функции спроса и затрат можно было считать фиксированными. Следовательно, задача состоит в отыскании функции  на которой функция
на которой функция

| (19 |
достигает своего максимального значения. При этом должны выполняться условия
 (20 (20
|
Из вариационного исчисления известно, что экстремум функционала (19) может достигаться лишь на решениях уравнения Эйлера
 (21 (21
|
Так как




После приведения подобных членов уравнение принимает вид

Общее решение этого уравнения дается формулой
 (22 (22
| |

| (23 |
а 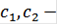 произвольные постоянные, определяемые условиями (20). Они имеют вид
произвольные постоянные, определяемые условиями (20). Они имеют вид
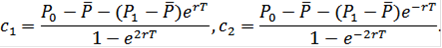 (24 (24
|
Таким образом, если решение задачи существует, то оно дается формулами (22) -(24). Чтобы удостовериться, что полученная функция действительно является решением, нужно еще проверить выполнение для нее достаточных условий экстремума функционала (19). Здесь я на этом на останавливаюсь.
Обоснованные цены по уровню актива
Под активом  понимается совокупность (в денежном выражении) всех принадлежащих данному предприятию материальных ценностей. Буду предполагать, что изменение
понимается совокупность (в денежном выражении) всех принадлежащих данному предприятию материальных ценностей. Буду предполагать, что изменение  пропорционально разности между предложением
пропорционально разности между предложением  и спросом
и спросом  с коэффициентом пропорциональности
с коэффициентом пропорциональности  Пусть, кроме того, изменение цены
Пусть, кроме того, изменение цены  также пропорционально отклонению актива
также пропорционально отклонению актива  от некоторого фиксированного уровня
от некоторого фиксированного уровня 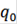 с коэффициентом пропорциональности
с коэффициентом пропорциональности  Следуя условиям задачи, можно записать
Следуя условиям задачи, можно записать
|
|
|

Здесь я учитываю, что предложение  и спрос
и спрос  являются функциями цены
являются функциями цены 
Рассмотрю простейший случай линейной зависимости  от цены
от цены 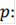

Тогда система уравнений приобретает вид
труд производительность дифференциальный уравнение
 (25 (25
|
Буду решать ее методом исключения. Дифференцируя второе уравнение и подставляя в первое, получу линейное уравнение с постоянными коэффициентами
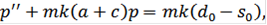
корнями характеристического многочлена которого будут  где
где  Частное решение
Частное решение  неоднородного уравнения легко вычислить методом неопределенных коэффициентов. Поэтому его общее решение запишу в виде
неоднородного уравнения легко вычислить методом неопределенных коэффициентов. Поэтому его общее решение запишу в виде

Тогда из второго уравнения (25) вычислю

Пусть начальная цена устанавливается равной  (то есть
(то есть  ). Тогда между ценой и уровнем актива выполняется соотношение
). Тогда между ценой и уровнем актива выполняется соотношение

Очевидно, эта кривая описывает динамическое равновесие рассматриваемого процесса. Подставляя в это уравнение значения  взятые в какой-то момент времени
взятые в какой-то момент времени  точно можно определить эту кривую (овал типа эллипса), отвечающую полученному значению
точно можно определить эту кривую (овал типа эллипса), отвечающую полученному значению  Ясно, что, желая находиться в указанном равновесном состоянии, я должен определять значение цены с помощью уровня актива по формуле
Ясно, что, желая находиться в указанном равновесном состоянии, я должен определять значение цены с помощью уровня актива по формуле

Заключение
Я рассмотрел использование дифференциальных уравнений в экономике. Изучив несколько моделей, а именно рост общественного благосостояния (модель Золотаса), динамику потребителей (модель Реденура). Самой широкомасштабной моделью оказалась теория фирмы. В ней я изучил, каким образом применяются дифференциальные уравнения в процессе естественного роста выпуска продукции, рекламе, динамике рыночной цены и т.д. Таким образом, дифференциальные уравнения являются одним из часто применяемых видов вычислений в деятельности человека.
|
|
|
Список литературы
1. Жегалов В.И., Киясов С.Н. Приложения обыкновенных дифференциальных уравнений, Издательство казанского государственного университета, 2007, 179 с.
2. Сабитов К.Б. Функциональные, дифференциальные и интегральные уравнения. «Высшая школа». Москва 2005, 671 с.
3. Самойленко А.М., Кривошея С.А., Перестюк Н.А. Дифференциальные уравнения: примеры и задачи. Москва 1989, 464 с.
4. Краснов М.Л., Киселев А.И., Макаренко Г.И. Обыкновенные дифференциальные уравнения. Москва 2009, 259 с.
5. Бугров Я.С., Никольский С.М. Высшая математика. Москва 2007, 511 с.
|
|
|


