 |
Замена переменной в определенном интеграле
|
|
|
|
Контрольная работа
По дисциплине:
«Высшая математика»
Тема:
«Длина дуги кривой в прямоугольных координатах»
Производная определенного интеграла по переменному верхнему пределу
Сформулируем следующее свойство определенных интегралов:
Пусть функция  непрерывна на
непрерывна на  . Составим для нее определенный интеграл
. Составим для нее определенный интеграл  . Пусть для определенности
. Пусть для определенности  на всем отрезке. Тогда с геометрической точки зрения составленный интеграл не что иное, как площадь криволинейной трапеции с основанием
на всем отрезке. Тогда с геометрической точки зрения составленный интеграл не что иное, как площадь криволинейной трапеции с основанием  , которая ограничена линией
, которая ограничена линией  .
.
Если в рассматриваемом интеграле заменить переменную интегрирования  на
на  , то величина его, очевидно, не изменится. Поэтому в дальнейшем для удобства будем считать, что площадь трапеции определяется интегралом
, то величина его, очевидно, не изменится. Поэтому в дальнейшем для удобства будем считать, что площадь трапеции определяется интегралом  .
.

Величина определенного интеграла зависит от значений верхнего и нижнего пределов интегрирования, то есть от длины основания криволинейной трапеции. Рассмотрим поэтому теперь случай, когда нижний предел интеграла фиксирован и равен  , а верхний может меняться, принимая значения
, а верхний может меняться, принимая значения  , где
, где  . В этом случае определенный интеграл будет соответствовать площади криволинейной трапеции, величина которой меняется. Зависеть эта площадь будет от значения
. В этом случае определенный интеграл будет соответствовать площади криволинейной трапеции, величина которой меняется. Зависеть эта площадь будет от значения  , то есть
, то есть  . Если
. Если  будет меняться непрерывно, то и площадь трапеции будет меняться непрерывно, то есть
будет меняться непрерывно, то и площадь трапеции будет меняться непрерывно, то есть  – непрерывная функция, которую можно дифференцировать.
– непрерывная функция, которую можно дифференцировать.
Теорема. Производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции, у которой переменная интегрирования заменена этим верхним пределом, то есть  или
или 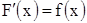 .
.
Для вычисления производной проделаем все стандартные операции. Зададим приращение аргументу:  , что, в свою очередь, приведет к приращению функции:
, что, в свою очередь, приведет к приращению функции:  . Так как
. Так как  , а
, а  , то приращение функции определяется выражением:
, то приращение функции определяется выражением:
|
|
|
 .
.
Применим к полученному выражению теорему о среднем в определенном интеграле:
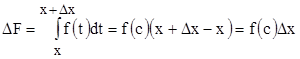 , где
, где  .
.
Составим отношение  . Чтобы получить производную
. Чтобы получить производную 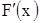 , перейдем в составленном отношении к пределу:
, перейдем в составленном отношении к пределу:  . Так как
. Так как  , то при стремлении
, то при стремлении  точка
точка  будет стремиться к
будет стремиться к  . Следовательно, вычисление предела приведет к выражению:
. Следовательно, вычисление предела приведет к выражению: 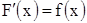 .
.
Из доказанной теоремы следует, что  – это первообразная от
– это первообразная от  , следовательно, определенный интеграл
, следовательно, определенный интеграл  также является первообразной от
также является первообразной от  , и вычислять его, очевидно, необходимо с помощью тех же приемов, что и неопределенный интеграл.
, и вычислять его, очевидно, необходимо с помощью тех же приемов, что и неопределенный интеграл.
Формула Ньютона–Лейбница
Вычисление определенного интеграла как предела интегральной суммы представляет собой довольно сложную задачу и может быть выполнено лишь в некоторых наиболее простых случаях. Однако полученная в п. 1 связь между определенным интегралом и первообразной позволяет получить простой метод для вычисления этих интегралов.
Теорема. Если  какая-либо первообразная от непрерывной функции
какая-либо первообразная от непрерывной функции  , то справедлива формула:
, то справедлива формула:  .
.
В предыдущем пункте было показано, что  – это первообразная от функции
– это первообразная от функции  . Но как было показано при изучении неопределенного интеграла, любая непрерывная функция имеет бесконечное множество первообразных, отличающихся друг от друга на постоянное слагаемое. Поэтому, если
. Но как было показано при изучении неопределенного интеграла, любая непрерывная функция имеет бесконечное множество первообразных, отличающихся друг от друга на постоянное слагаемое. Поэтому, если  какая-то другая первообразная от той же функции
какая-то другая первообразная от той же функции  , то
, то  .
.
Оказывается, что в случае определенного интеграла постоянную  можно вычислить. Действительно, так как
можно вычислить. Действительно, так как  может принимать любые значения между
может принимать любые значения между  и
и  (п. 1), то пусть
(п. 1), то пусть  . Тогда:
. Тогда:  . Но определенный интеграл с равными пределами равен нулю, следовательно,
. Но определенный интеграл с равными пределами равен нулю, следовательно,  . Значит,
. Значит,
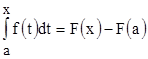 .
.
Положим теперь, что  , тогда
, тогда
 .
.
Полученное выражение называется формулой Ньютона – Лейбница. Другая форма записи этого выражения следующая:
|
|
|
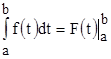 .
.
Обычно в полученных выражениях переменная интегрирования обозначается буквой  .
.
Таким образом, чтобы вычислить определенный интеграл, необходимо найти любую первообразную от  и вычислить разность ее значений в верхнем и нижнем пределах интегрирования. Полученная простая формула позволяет легко находить решения многих математических и прикладных задач, связанных с вычислением определенного интеграла.
и вычислить разность ее значений в верхнем и нижнем пределах интегрирования. Полученная простая формула позволяет легко находить решения многих математических и прикладных задач, связанных с вычислением определенного интеграла.
Замена переменной в определенном интеграле
При изучении неопределенного интеграла было показано (п. 5.4), что одним из наиболее часто встречающихся методов его вычисления является замена переменных. Так как вычисление определенного интеграла, согласно формуле Ньютона – Лейбница, также связано с нахождением первообразной, то метод замены переменной применим и в нем, однако при этом имеются некоторые особенности. В неопределенном интеграле замена переменной приводила в конце вычислений к обратной замене, в определенном же, оказывается, можно обойтись без этого.
Теорема. Если в определенном интеграле  , где
, где 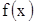 непрерывна на
непрерывна на  , сделать замену переменной
, сделать замену переменной  и при этом:
и при этом:
1)  ,
,  ;
;
2)  и
и  непрерывны на
непрерывны на 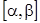 ;
;
3)  непрерывна на
непрерывна на 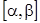 и при изменении
и при изменении  от
от  до
до 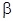 не выходит за пределы отрезка
не выходит за пределы отрезка  ,
,
то  .
.
Пусть  – какая-то первообразная от
– какая-то первообразная от 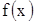 , тогда
, тогда  . Согласно формуле Ньютона – Лейбница, получим соответствующий определенный интеграл:
. Согласно формуле Ньютона – Лейбница, получим соответствующий определенный интеграл:  . Но, как было показано в п. 5.4, в неопределенном интеграле можно сделать замену переменной
. Но, как было показано в п. 5.4, в неопределенном интеграле можно сделать замену переменной  , тогда
, тогда  . В этом случае соответствующий определенный интеграл будет иметь вид:
. В этом случае соответствующий определенный интеграл будет иметь вид:
 .
.
У обоих определенных интегралов правые части равны, следовательно, равны и левые части:
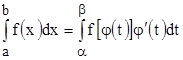 ,
,
что и требовалось доказать.
Из доказанной теоремы следует, что при замене переменной в определенном интеграле должны поменяться пределы интегрирования, и обратная замена здесь уже не нужна, так как и при старой и при новой переменной в ответе получается одно и то же число.
|
|
|
12 |


