 |
Интегрирование по частям в определенном интеграле
|
|
|
|
Пусть даны функции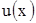 
и 
, которые непрерывны со своими производными на 
. Составим их произведение и продифференцируем его:
.
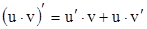Возьмем от обеих частей полученного равенства определенные интегралы:
.
Но 
, 
, 
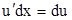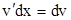. Следовательно, 
, откуда: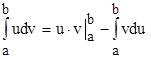 
. Так же как и в неопределенном интеграле, данная формула требует правильного выбора множителей 
и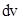 
.
Длина дуги кривой в прямоугольных координатах
При вычислении длины кривой линии может быть использована та же методика, что и при вычислении площадей криволинейных трапеций, то есть кривую разбивают на такие малые участки, длину которых можно посчитать геометрическими методами.
Определение. Длиной дуги кривой линии называют предел, к которому стремится длина вписанной в нее ломаной линии при неограниченном увеличении числа ее звеньев и при стремлении длины наибольшего звена к нулю.
Итак, пусть кривая линия 
описывается функцией 
на отрезке 
. При этом пусть 
непрерывна на этом отрезке вместе со своей производной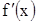 
. Разобьем кривую на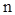 
частичных дуг точками 
. Соединив начало и конец каждой частичной дуги хордой, получим в результате вписанную ломаную линию, длина которой равна сумме длин ее звеньев:
.
Обозначим: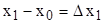 
, 
,…, 
,…, 
. Кроме того, 
, 
,…, 
,…, 
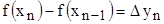. В таком случае 
можно рассматривать как гипотенузу прямоугольного треугольника и поэтому
.
Согласно теореме Лагранжа о среднем
, где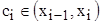 
,
следовательно,
.
Отсюда длина ломаной линии равна
.
Переходя к пределу в данной интегральной сумме, когда число звеньев ломаной стремится к бесконечности, а длина наибольшего звена стремится к нулю, получаем длину кривой линии в прямоугольной системе координат:
|
|
|
.
Данный интеграл существует, поскольку по условию производная 
непрерывна.
Из полученной формулы можно получить выражение для дифференциала дуги, которое используется как в математике, так и в некоторых задачах теоретической механики. Пусть положение правого конца кривой линии является переменной величиной, тогда ее длина будет функцией точки, в которой она заканчивается, то есть
.
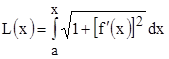Возьмем производную данного интеграла по переменному верхнему пределу (п. 1.):
.
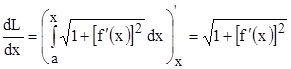Отсюда следует, что
.
Длина дуги кривой при ее параметрическом задании
Рассмотрим теперь случай, когда кривая, длину которой необходимо вычислить, задана параметрически, то есть 
при этом изменение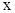 
от 
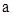до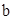 
приводит к изменению 
от 
до 
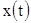. Пусть функции 
и 
непрерывны вместе со своими производными на отрезке 
и при этом 
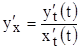. Тогда 
, а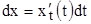 
. Подставим значение данной производной и дифференциала в формулу для длины дуги в прямоугольной системе координат (п. 5):
.
В случае пространственной кривой ее параметрическое задание будет выглядеть следующим образом:
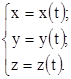
Если указанные функции непрерывны вместе со своими производными на отрезке , то можно доказать, что длина данной кривой вычисляется по формуле
.
Длина дуги в полярной системе координат
Если кривая задана в полярной системе координат, то она описывается функцией 
, где 
. Пусть 
непрерывна вместе со своей производной на отрезке 
.
Перейдем от полярной к прямоугольной системе координат: 
. Но так как , то получаем, что 
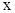. Иначе говоря, и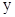 
выражены через параметр 
, поэтому можно воспользоваться формулой для длины дуги при ее параметрическом задании (п. 6.):
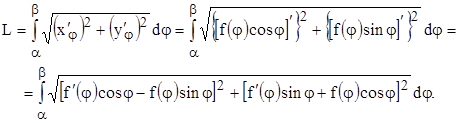
Возведя в квадрат выражения в скобках и выполнив элементарные преобразования, получаем:
.
|
|
|
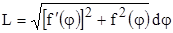Обычно данную формулу записывают следующим образом:
.
|
|
|
12 |
