Зубчатые передачи с зацеплением М. Л. Новикова

Расчет на контактную прочность цилиндрических косозубых зубчатых передач.

Вследствие наклонного расположения зубьев в косозубом зацеплении одновременно находятся несколько пар зубьев, что уменьшает нагрузку на один зуб и снижает динамические нагрузки. Расчет на прочность косозубых передач ведут по формулам эквивалентных прямозубых передач с введением в них поправочных коэффициентов, учитывающих особенности работы. По условиям прочности габариты косозубых передач получаются меньше, чем прямозубых.

Проектировочный расчет. Аналогично расчету прямозубой передачи определяют межосевое

расстояние для стальной косозубой передачи.

 

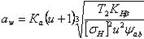
Проверочный расчет. Аналогично расчету прямозубой передачи находят контактные напряжения в поверхностном слое косых зубьев.

σн = Zσ /aw√KнT1(U+1)³/b2U ≤ [ σ ] н

50. Расчет на изгиб цилиндрических косозубых зубчатых передач.

Выполнение условия прочности на изгиб зубьев шестерни и колеса косозубой передачи проверяют аналогично расчету прямозубой передачи σ _F = K_F*F_{t *}Y_Fs*Y_{β *}Y _ε<=[σ]_F. Коэффициент Y_Fs формы зуба и концентрации напряжений, выбирают по эквивалентному числу зубьев z_v. Коэффициент Y _β, учитывающий наклон зуба в косозубой передаче, вычисляют по формуле:

Y_β = 1- β/100⁰ при условии Y_β >=0,7

Коэффициент Y _ε, учитывающий перекрытие зубьев в косозубой передаче: Y _ε = 0,65.

 

Шевронные цилиндрические передачи.

Шевронные цилиндрические передачи обладают крайне высокой плавностью работы. Шестерни этих передач представляют собой сдвоенные косозубые шестерни, но они имеют больший угол зубьев, чем косозубые. Вследствие разного направления зубьев на полушевронах осевые силы F_a/2 взаимно уравновешиваются на колесе и на подшипники не передаются. Это обстоятельство позволяет принимать у шевронных колес угол наклона зуба β = 25...40°, что повышает прочность зубьев и плавность передачи. В редукторах с шевронной передачей быстроходный вал передачи устанавливают на плавающих, обычно цилиндрических роликоподшипниках, что обеспечивает самоустановку вала по оси и одинаковую нагрузку полушевронов. Для опор плавающих валов шевронных передач применяют радиальные подшипники с короткими цилиндрическими роликами, также первоначально легкой серии.

Геометрический и прочностной расчеты шевронной передачи аналогичны расчетам косозубой передачи. Для шевронной пе­редачи коэффициент ширины обода колеса ψ_α = 0,4...0,8

Зубчатые передачи с зацеплением М. Л. Новикова

Эвольвентное зацепление, распространенное в современном машиностроении, является линейчатым, так как контакт зубьев происходит по линии (практически по узкой площадке), расположенной вдоль зуба (рис. 10.6). Вследствие малого приве­денного радиуса кривизны контактная прочность эвольвентного зацепления сравнительно невысока, поэтому для современных мощных передач важен вопрос повышения несущей способности зубчатых передач.

М. Л. Новиковым было предложено новое точечное за­цепление, β котором профили зубьев колес в торцовом сече­нии очерчены по дугам окружности. Зуб шестерни делается выпуклым, а зуб колеса — вогнутым, что увеличивает их приведенный радиус кривизны, значительно повышая контакт­ную прочность передачи.

В зацеплении Новикова контакт зубьев происходит в точке и зубья касаются только в момент прохождения профилей через эту точку, а непрерывность передачи движения обес­печивается винтовой формой зубьев.

 

53. Назначение, классификация конических передач. Геометрия зацепления. Силы в зацеплении. Эквивалентное колесо.

Конические зубчатые колеса применяют в передачах, когда оси валов пересекаются под углом ε. Наибольшее распространение имеют передачи с углом, ε = 90°, которые и рассмотрены ниже. Конические колеса бывают с прямыми, круговыми и редко с шевронными зубьями.

Конические прямозубые передачи имеют начальный линейный, а передачи с круговыми зубьями — точечный контакт в зацеплении.

Конические колеса с круговыми зубьями по сравнению с прямозубыми обладают большей несущей способностью, работают плавно и с меньшим шумом.

Сопряженные колеса с круговым зубом имеют противоположное направление линии зубьев правое и левое, если смотреть со стороны вершины конуса. Шестерни выполняют с правым зубом, колеса — с левым. В конических передачах шестерню располагают консольно.

Передаточное число. u = n ₁/ n ₂ = d_{e 2}/ d_{e 1} = tg δ ₂ =1/ tg δ ₁ = z ₂/ z ₁.

где de 1, de 2 и δ 1 и δ 2 — соответственно, внешние делительные диаметры

и углы делительных конусов шестерни и колеса.

Для конической прямозубой передачи рекомендуют и = 2...3;

при колесах с круговыми зубьями и до 6,3.

123Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: