 |
трехфазного асинхронного двигателя
|
|
|
|
электрических двигателей
Механическая характеристика рабочей машины - зависимость статического момента сопротивления «Мс», создаваемого рабочими органами машины, от угловой скорости вала машины или частоты его вращения:
Мс= ¦(w) или Мс= ¦(n).
 w; n; М
w; n; М




 wм; nм; Мс
wм; nм; Мс




 ЭД
ЭД

 Раб. машина
Раб. машина
 |
Рис.5 Схема привода рабочей машины
Мс= ¦(w) часто используется для расчета времени разгона и торможения, дает представление о моментах трогания машины с места (рис.6)
 Мс Мс.н.
Мс Мс.н.
 |
М0
 wн w
wн w
Рис.6 График механической характеристики рабочей машины
Для каждой машины имеется своя характеристика. Но некоторые схожие машины одинакового принципа действия можно объединить в отдельные группы идеализированных механических характеристик. Для всех машин получено обобщенное уравнение вида:
Мс= Мо+ (Мс.н+ Мо)× 
 (1)
(1)
где Мс – момент сопротивления при данной угловой скорости «w»;
Мо – момент сопротивления при трогании, т.е. при «w=0»;
Мс.н – номинальный момент сопротивления, т.е. при номинальной
угловой скорости wн;
w - текущее значение угловой скорости;
х – коэффициент, характеризующий изменение момента сопротивления при изменении угловой скорости - х = -1; 0; 1; 2.
Это эмпирическое уравнение справедливо для разных групп рабочих машин и распределение по группам определяется принятым значением коэффициента «х». В зависимости от «х» рабочие машины по механическим характеристикам могут быть разбиты на 4 группы (рис.5):
1. При х = 0 Мс = Мс.н = const. Такой характеристикой обладают машины, момент сопротивления которых не зависит от скорости вращения вала, например, подъемные краны, лебедки, поршневые насосы при неизменной высоте подачи, конвейеры с постоянной массой передвигаемого материала.
|
|
|

 Мс 3, х=2
Мс 3, х=2

 2, х=1
2, х=1
1, х=0
 | |||||
 | 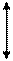 | ||||
 DМс dМс 4, х=-1
DМс dМс 4, х=-1




 Dw
Dw
 Мтр М0 dw
Мтр М0 dw

 w
w
Рис.7 Механические характеристики рабочих машин
в зависимости от коэффициента «х».
2. х =1 – линейно возрастающая механическая характеристика - момент сопротивления линейно возрастает в зависимости от угловой скорости.
Обычно такая характеристика у машин, работающих с небольшой скоростью – вакуумные насосы доильных машин и др.
3. х=2 – нелинейно возрастающая (параболическая) характеристика. Обычно называют вентиляторной, поскольку у вентиляторов момент сопротивления зависит от квадрата скорости. Также - центробежные насосы, молочные сепараторы, молотильные барабаны при работе на холостом ходу и др.
4.х=-1 – нелинейно-спадающая характеристика. Момент сопротивления изменяется обратно-пропорционально скорости, а мощность, потребляемая механизмом, остается постоянной.
Такой характеристикой обладают некоторые токарные, расточные, фрезерные и другие металлорежущие станки, нории, элеваторы.
Реальные характеристики несколько отличаются от этих идеализированных, но условное деление в данном случае допускается.
Степень изменения скорости с изменением момента для различных машин различна и характеризуется жесткостью их механических характеристик.
Жесткость механической характеристики – отношение разности моментов к соответствующей разности угловых скоростей
bс = (Мс2 – Мс1)/(w2 - w1) = DМс/Dw (2)
В случае нелинейных характеристик их жесткость непостоянна и определяется в каждой точке как производная момента по угловой скорости
bс = dМc/dw(3)
При х=0 bс = 0 – абсолютно жесткая характеристика;
х=1 bс > 0 – постоянная (const);
х=2 bс = DМс/Dw = tga
х=-1 bс = DМс/Dw < 0.
Механической характеристикой электродвигателя называют зависимость вращающего или тормозного момента от скорости
|
|
|
М = ¦(w) или М = ¦(w)
Механические характеристики электродвигателей могут быть естественные и искусственные.
Естественной механической характеристикой обладает каждый ЭД. Она получается при номинальных параметрах питающей сети и электродвигателя, т.е. выполняются условия
U =Uн = const; f = fн = сonst; r2 = const – сопротивления, введенные в цепь ротора, отсутствуют, т.е. R=0;
Соединений обмоток ЭД соответствует указанной схеме завода-изготовителя.
Искусственные характеристики получаются при изменении параметров сети или схемы соединения обмоток, включения добавочных сопротивлений в обмотки статора или ротора ЭД. Эти характеристики создаются специально, когда естественная характеристика ЭД не удовлетворяет требованиям приводимого в движение механизма или машины, например, пуск двигателя с тяжелым механизмом.
Лекция №2
По жесткости механические характеристики ЭД можно разделить на четыре основные категории.
1. Абсолютно жесткая – это характеристика, при которой скорость с изменением момента остается постоянной (синхронные двигатели, двигатели постоянного тока с компаундной – смешанной, обмоткой возбуждения). Для них b = ¥ (рис.8, характеристика 1).






 М 3 в 2 1 1а
М 3 в 2 1 1а
 |
 5
5
 4
4
2а

 Мн С
Мн С
 |
 wн а w
wн а w
Рис.8 Механические характеристики электрических двигателей
2. Жесткая – характеристика, при которой незначительное изменение скорости вызывает значительное изменение момента (кривая 2, рис.8).
Такой характеристикой обладают «шунтовые» двигатели постоянного тока (с параллельной обмоткой возбуждения), а также асинхронные двигатели в пределах рабочей части механической характеристики.
3. Мягкая – характеристика, при которой с изменением момента скорость изменяется значительно. Ею обладают «сериесные» двигатели постоянного тока (с последовательной обмоткой возбуждения).
4. Абсолютно мягкая – характеристика, при которой момент двигателя с изменением угловой скорости остается постоянным.
Такой характеристикой обладают двигатели постоянного тока независимого возбуждения при питании их от постороннего источника тока. Их называют специальными характеристиками. Они имеют особую форму, приспособленную для тех или иных рабочих машин. Примером может служить кривая 5 (рис.8) –«экскаваторная» характеристика.
|
|
|
Статическая устойчивость электропривода
Работе ЭД и рабочей машины в установившемся режиме соответствует равновесие момента сопротивления машины и вращающего момента двигателя при определенной скорости, возникает динамическое равновесие, т.е.
М = Мс
При изменении под влиянием каких-либо внешних причин скорости двигателя и момента, они автоматически изменяются, восстанавливая нарушенное равновесие. Привод будет продолжать устойчиво работать при другой скорости с новым значением момента.
Для восстановления равновесия во всех неэлектрических двигателях требуется участие специальных регуляторов, которые воздействуют на источник энергии, увеличивая или уменьшая подачу воды, топлива, пара и др.
В электрических двигателях роль автоматического регулятора выполняет ЭДС ротора двигателя. Это очень ценное свойство.
Привод считается статически устойчивым, если в точке установившегося режима выполняется условие
bс - b > 0
или dМс/dw - dМ/dw > 0
Знание критерия статической устойчивости ЭП позволяет в каждом конкретном случае сравнительно легко определить, будет ли рассматриваемый ЭП работать устойчиво.
Пример.
Если использовать асинхронный двигатель с короткозамкнутым ротором и нагрузить его постоянным моментом (рис.7), то в т. «а» разность коэффициентов жесткости будет
bс - b > 0
т.е. dМс/dw - dМ/dw > 0
или 0/dw - (- dМ/dw) = 0 + b > 0, т.е. режим работы ЭП устойчивый.




 М, Мс 2 3
М, Мс 2 3
в







 Мс а DМс=0
Мс а DМс=0
 -DМ +Dw
-DМ +Dw


 -DМ
-DМ


 -Dw
-Dw
Dw
 w
w
Рис.9 Определение статической устойчивости электропривода
В точке “в”: dМс/dw - dМ/dw = 0 - b < 0, т.е. режим работы неустойчивый.
При работе того же двигателя с механизмом, обладающим вентиляторной характеристикой легко доказать, что во всех точках работа будет устойчивой (доказать самостоятельно по рис.9, кривые 2 и 3).
|
|
|
Типы электродвигателей и номинальные режимы
Номинальные режимы работы электродвигателя устанавливаются относительно работы его на высоте до 1000 м над уровнем моря при температуре окружающей среды +40°С.
Номинальной мощностью ЭД (Рн) называется полезная мощность на валу двигателя при номинальных параметрах частоты вращения (nн) и напряжении в сети (Uн) в соответствии с паспортными данными двигателя. Выражается в ваттах (Вт), киловаттах (кВт) или мегаваттах (МВт).
 |
Промышленность выпускает 95% двигателей переменного тока бесколлекторных асинхронных трехфазных с короткозамкнутым ротором.
Номинальный вращающий момент (Мн) – момент, развиваемый двигателем при номинальной мощности (Рн), частоте вращения (nн) и напряжении (Uн) указанными в паспорте электродвигателя
Мн= 9.55×Рн/nн н×м (4)
Номинальная частота (nн), номинальное напряжение (Uн), номинальный ток (Iн) и номинальный КПД (hн) – указанные в паспорте двигателя, при условии, что все остальные величины, характеризующие режим работы, имеют также номинальные значения.
Принцип работы трехфазного асинхронного электродвигателя
Принцип известен из курсов физики и электротехники. Он основан на электромагнитной индукции.
Конструктивно двигатель состоит из двух основных узлов:
1 – неподвижный – статор;
2 – вращающийся (подвижный) – ротор.
Статор. Внутри станины, цилиндра из чугуна или алюминия, помещен сердечник, набранный из колец, штампованных из листовой электротехнической стали толщиной 0.35 - 0.5 мм, изолированных друг от друга для уменьшения потерь на вихревые токи.
На внутренней поверхности колец выполнены пазы, предназначенные для укладки обмоток статора. Статор имеет три обмотки (по числу фаз) сдвинутые в пространстве на угол 120° друг относительно друга.
Если эти обмотки подключить к цепи переменного тока, то максимальное значение тока в каждой обмотке и создаваемый ими магнитный поток будут сдвинуты на 120° во времени и будут появляться в разные моменты времени через 1/50с при частоте тока 50Гц. Поэтому, оказывается, что максимальное значение магнитного потока движется по окружности статора – создается как бы непрерывно вращающееся магнитное поле.
Вспомним из электротехники как создается вращающееся магнитное поле.
Простейшая обмотка статора состоит из трех катушек смещенных, как уже говорилось, на 120° в пространстве друг относительно друга. Для удобства будем считать, что каждая катушка имеет только один виток. Обозначим начала витков А, В, С, а концы – Х, У, Z (рис.10).
 А
А
У Z
С В
Х
Рис.10 Обозначение обмоток и размещение их в статоре
|
|
|
Изменение ЭДС в каждой фазе сети происходит по синусоидальному закону и сдвинуто в каждой фазе по отношению к предыдущей на 1/3 периода Т или на угол 120°= 2/3p, т.е.:
ЭДС фазы А еА= Еm×sinwt
фазы В еВ = Еm×sin(wt – 2/3p)
фазы С еС = Еm×sin(wt – 4/3p)
где Еm –максимальное или амплитудное значение ЭДС, одинаковое по величине для всех трех фаз: ЕmА= ЕmВ = ЕmC = Еm.
Тогда, совмещенная волновая диаграмма, показывающая изменение ЭДС во всех трех фазах сети переменного тока, будет иметь вид (рис.11).
Соответственно будет изменяться и магнитный поток, создаваемый в каждой фазе, т.е.:
ФА = Фm×sinwt;
ФВ = Фm×sin(wt-2/3p);
ФС = Фm×sin(wt-4/3p).
 +е А В С
+е А В С
Еm Еm Еm
p wt
-е
t1
t2
t3
T
Рис.11 Изменение ЭДС в обмотках статора
Таким образом, в каждой фазе (катушке) статора двигателя, вектор магнитной индукции изменяется по синусоидальному закону, но не вращается вокруг оси. Условимся считать положительным направление ЭДС и тока от конца каждой фазы к ее началу.
Рассмотрим направление ЭДС, тока и вектора магнитной индукции в фазе статора «А-Х» (рис.12) при значениях ЭДС фазы «А» от еА= +Еm до еА= -Еm.
Как видно из рис.12 и рис.13, при изменении направления тока в катушке направление вектора магнитной индукции меняется на противоположное (по правилу правой руки).

 А А
А А
ФА ФА
Х Х
Рис.12 Направление магнитной Рис.13 В момент времени, когда
индукции при еА= +Еm еА= -Еm.
Но при одновременном включении трех фаз статора на переменный трехфазный ток результирующий вектор магнитного потока, являющийся геометрической суммой векторов всех трех фаз, будет вращаться.
В этом нетрудно убедиться, рассмотрев направление ЭДС, токов и векторов индукции в каждой фазе статора в моменты времени t1, t2 и t3, отличающиеся на волновой диаграмме на 1/3 периода Т.
Из волновой диаграммы (рис.11) видно, что в момент времени t1 направление ЭДС в фазе «А» положительно и, следовательно, направление тока в фазе «А-Х» статора, подключенной к фазе «А» сети тоже будет положительным, т.е. от конца катушки Х к ее началу А (рис.14).
А




 Y Z
Y Z
 |  | ||||
 |


 N S
N S
C B
 |
X
В фазах В и С сети направление ЭДС отрицательно и, соответственно, направление токов в фазах В-У и С-Z статора, также отрицательно, т.е. ток направлен от начал катушек В и С к их концам У и Z.
ЭДС в фазе А равна Еm, в фазе В – 0.5Еm, в фазе С – 0.5Еm. Следовательно и магнитные индукции Ф в момент времени t1 в фазах будут:
ФА=Фm; ФВ=+0.5Фm; ФС=+0.5Фm.
При их геометрическом сложении сумма магнитных индукций будет 1.5Фm.

 ФВ=0.5Фm
ФВ=0.5Фm






 0.5Фm ФА=Фm
0.5Фm ФА=Фm
ФС=0.5Фm
1.5Фm
 |
Рис.15 Сумма векторов магнитных индукций трех обмоток статора
В момент времени t2, который отличается от t1 на t2-t1=1/3T, направление ЭДС в фазе В будет положительным, а в фазах А и С - отрицательным. Соответственно будут направлены и токи в фазах статора: в фазе В-У – от конца к началу, а в фазах С-Z и А-Х - от начал к концам.
В результате геометрического сложения векторов магнитных индукций всех трех фаз результирующий вектор оказывается смещенным на 120° (1/3 оборота) (рис.16) по отношению к положению, которое он занимал в момент времени t1.
А
 N
N
 У Z
У Z

C В
Х
S
Рис.16 Расположение полюсов в статоре в момент времени t2.
В момент времени t3 направление ЭДС сети, соответствующие им токи и магнитные индукции, будут также отличаться от момента времени t2 на 1/3 периода Т или на 120° (рис.17).


 S А
S А
 |
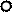

 У Z
У Z
 |  |
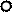 С В
С В
Х N
Рис.17 Расположение полюсов в статоре в момент времени t3.
Как видно из рассмотренного примера, магнитное поле, создаваемое трехфазным переменным током при протекании через обмотки статора, имеет два полюса или одну пару полюсов р=1.
За время (t2-t1) ось поворачивается на 1/3 оборота или, за время равное периоду переменного тока Т, наодин оборот. При частоте тока сети ¦1=50Гц число периодов в минуту составит 60צ1=3000 мин-1, т.е. магнитное поле, имеющее одну пару полюсов р=1, за минуту совершит 3000 оборотов.
Таким образом, при увеличении числа пар полюсов частота вращения будет уменьшаться согласно выражения
n0 = 60צ1/р мин-1 (5)
Скорость вращающегося магнитного поля статора n0 называется синхронной потому, что она изменяется одновременно (синхронно) с частотой питающей сети. Следовательно, ряд синхронных скоростей магнитного поля статора при ¦1=50Гц в зависимости от числа пар полюсов, будет следующим:
| р = 1 | р = 2 | р = 3 | р = 4 | р = 5 | р = 6 |
| n0=3000 | n0=1500 | n0=1000 | n0=750 | n0=600 | n0=500 |
Лекция № 3
Ротор. Внутрь статора помещают стальной цилиндр, вращающийся на подшипниках. Вдоль ротора выполнены пазы в которые укладываются обмотки ротора. Они выполняются в виде «беличьего» колеса, т.е. короткозамкнутые – короткозамкнутый ротор.
В электродвигателях большой мощности одни концы обмоток замыкают накоротко, а другие выводят на контактные кольца, подключаемые через реостат. Это двигатели с контактными кольцами или с фазным ротором.
Магнитный поток статора (Ф), вращаясь в пространстве с постоянной скоростью, наводит в обмотках ротора ЭДС (Е2), которая создает в короткозамкнутой обмотке ротора ток ротора (I2).
Вращающееся поле статора (Ф), взаимодействуя с током ротора (I2), создает вращающий момент (М), (направление которого определяется по правилу левой руки), увлекающий ротор в направлении вращения поля.
При этом скорость вращения ротора всегда будет меньше скорости вращения магнитного поля статора, т. к., если бы ротор вращался со скоростью равной скорости вращения магнитного поля статора, то его обмотки были бы неподвижными по отношению к линиям поля статора, не пересекали бы их и в обмотке ротора не индуктировалась бы ЭДС (Е2) и, следовательно, не было бы тока ротора (I2), т.е. отсутствовал бы вращающий момент.
Таким образом, в отличие от синхронной скорости вращающегося магнитного поля статора (n0), ротор двигателя вращается с асинхронной скоростью (n), отставая от частоты вращения магнитного поля статора. Степень отставания ротора относительно вращающегося поля статора характеризуется скольжением ротора:
S = 
или n = n0(1 – s).
Величина скольжения обычно невелика и при работе ЭД изменяется незначительно (0.05-0.12) в зависимости от нагрузки на двигатель.
Скольжение имеет большое значение для асинхронных двигателей, определяя многие его свойства. Следует иметь в виду, что при s=1 ротор электродвигателя неподвижен. При уменьшении скольжения частота вращения ротора возрастает и при s=0 ротор достигает наибольшей (синхронной) частоты вращения. В этом случае, частота вращения магнитного поля статора и частота вращения ротора одинаковы.
Обмотки статора могут соединяться либо в звезду, либо в треугольник (рис.18).





 А В С А В С
А В С А В С
Y D
 | |||
 | |||


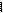








 C1 С6 С1
C1 С6 С1
 |  |
C6 C4









 C5 С3 С4
C5 С3 С4
С5 С2

 C3 C2 Uф=220 В
C3 C2 Uф=220 В
 Uл=380 В
Uл=380 В
 |











 или или
или или



















 С1 С2 С3 С1 С2 С3
С1 С2 С3 С1 С2 С3
 |  |  | |||||||||
 |  |  | |||||||||







 С4 С5 С6
С4 С5 С6

 С4 С5 С6
С4 С5 С6
клеммная колодка клеммная колодка

С1 С2 С3 С1 С2 С3
С4 С5 С6
С4 С5 С6
Рис.18 Соединение обмоток в «звезду» и в «треугольник».
Механическая характеристика асинхронного двигателя
Методика вывода и построения механической характеристики двигателя заключается в том, что в уравнении момента все составляющие в функции электрических величин заменяются на составляющие в функции скольжения.
Представим асинхронный двигатель в виде схемы (рис.19)


 С А В
С А В
 w1 Е1
w1 Е1
r1 U1
 х1 обмотка статора
х1 обмотка статора
 |  | ||||
 |





 r2 Е2 контактные кольца
r2 Е2 контактные кольца


 обмотка ротора х2 U2
обмотка ротора х2 U2




 регулировочный
регулировочный







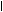
 реостат (R)
реостат (R)
Рис. 19 Схема асинхронного двигателя с фазным ротором
где U1 и U2 – напряжения на обмотках статора и ротора соответственно;
Е1 и Е2 – ЭДС в обмотках статора и ротора соответственно;
w1 – количество витков обмотки статора;
r1 и r2 – активное сопротивление обмотки статора и ротора;
х1 и х2 – индуктивное сопротивление обмотки статора и ротора:
х2= 2pצ2×L2 = 2pצ1×L2×s (6)
где ¦2 – частота тока в роторе;
L2 – индуктивность обмоток ротора;
2pצ1×L2 = х20 – индуктивное сопротивление неподвижного ротора.
Обычно величина постоянная для данного двигателя.
Тогда: х2 = х20×s (7)
Аналогично ЭДС вращающегося ротора: Е2 = Е20×s (8)
где Е20 – ЭДС неподвижного ротора. Величина постоянная для опреде-
ленного двигателя. В паспорте двигателя указывается как Uротора;
R – сопротивление одной фазы пускорегулирующего реостата.
Уравнение естественной механической характеристики
асинхронного двигателя
Естественная механическая характеристика определяется или рассчитывается при условии постоянства следующих параметров
U1 = Uн = const; I1 = Iн =const; ¦1 = ¦н = const; r2 = const; R = 0.
Искусственная механическая характеристика (промежуточная) получится при изменении хотя бы одного из этих параметров.
Из электротехники известно
М=с×Ф×I2×cosy2 (9)
где с – коэффициент, учитывающий конструктивные особенности
двигателя;
Ф – результирующий вращающий магнитный поток;
I2×cosy2 - активный ток ротора;
y2 - угол сдвига между ЭДС (Е2), наведенной в роторе и током
ротора (I2).
Известно, что магнитный поток (Ф), полный ток ротора (I2) и cosy2 являются функциями скольжения, т.е.
Ф =¦(s); I2 = ¦(s); cosy2 = ¦(s).
Также из электротехники известно, что
Е1=4.44×w1צ1×k1×Ф (10)
где k1 – обмоточный коэффициент.
Откуда
Ф=  (11)
(11)
Из электротехники же известно, что
I2= 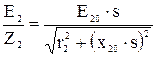 (12)
(12)
cosy2=  (13)
(13)
Отношение Е1/Е20 = k - называется коэффициентом трансформации
А также, для короткозамкнутого двигателя
U1 = Е1 + I1×Z1 @ Е1, т.е.
U1@Е1 или U21@Е21 (14)
Подставляя (11), (12), (13) в уравнение (9) и учитывая (14), получим
 (15)
(15)
обозначим, как величины постоянные 
Тогда, уравнение (15) примет вид
М=с1×U21×


