к 12-месячным цепным средним.

Метод корригированных средних принимает во внимание и правильно учитывает влияние длительно действующих факторов только тогда, когда тенденция развития, вызванная влиянием этих факторов, прямолинейна. Однако тенденция в развитии явлений, может быть какой угодно.

По сравнению с методами обычных и корригированных средних данный метод имеет то преимущество, что позволяет учесть влияние длительно действующих факторов независимо от того, какова форма тенденции развития - прямолинейная или криволинейная.

Ход работы

1. Вычисляют 12-месячные цепные средние. Следует отметить, что при этом цепные осреднения не могут быть вычислены для первых шести месяцев первого года и за последние 5 месяцев последнего года. Усреднение на этом этапе работы проводится для устранения временно действующих и сезонно действующих причин. Следовательно в каждой из 12-месячной цепной средней осталось только влияние длительно действующих факторов.

2. Делят фактические данные каждого месяца отдельно на 12-месячные цепные средние и полученный результат умножают на 100. Это действие производится для исключения учета влияния временно действующих и сезонно действующих факторов. Следует напомнить, что фактические данные отражают на себе влияние как длительно действующих, так и временно и сезонно действующих причин, а 12-месячные цепные средние - влияние только длительно действующих причин. Следовательно принимая за основание деления 12-месячные цепные средние, исключают влияние временно и сезонно действующих причин.

3. Полученные таким образом результаты усредняют помесячно и получают 12 месячных средних. Это делается для устранения временно действующих случайных причин. Следовательно в полученных месячных средних осталось влияние только сезонно действующих причин.

4. Производят усреднение 12-месячных средних и получают общую среднюю. В этой средней устранено влияние сезонно действующих причин.

5. Находят индексы сезонных колебаний путем отношения каждой из месячных средних к общей средней, результат умножают на 100 для получения результатов в процентах.

 

Ошибки, допускаемые при количественной характеристике

сезонных колебаний

 

1. Иногда, для того чтобы выразить сезонные колебания, пользуются месячными экстенсивными показателями. Для этого годовое число принимают за 100 %, а месячные числа распре-деляют в процентах по отношению к итогу. Этот метод мало чем отличается от метода, описанного под названием “Метод обычных средних”. Однако существуют два обстоятельства, дающих основание предпочитать метод обычных средних применению метода экстенсивных показателей. Во-первых, базой для сравнения месячных средних при пользовании методом обычных средних является среднегодовой уровень равный 100 %, а при методе экстенсивных показателей 8,33=10/12. Во-вторых, при помесячных процентных показателях не учитывается различная длина месяца. В-третьих, тогда, когда в развитии изучаемого явления сказывается наличие длительно действующих факторов, следует применять иные методы количественной характеристики сезонности (метод корригированных средних, метод отношений).

2. Недооценка фактора сезонности может привести к неправильным выводам. Например, было отмечено, что такой антропометрический признак как “вес” имеет более высокие значения осенью и зимой и более низкие весной и летом.

3. Наиболее подходящим способом графического изображения сезонных колебаний является построение круговой линейной диаграммы.

 

Кластерный анализ

Кластерный анализ является одним из базовых методов распознавания образов без обучения. Методами кластерного анализа решается задача разбиения (классификации, кластеризации) множества объектов таким образом, чтобы все объекты, принадлежащие одному кластеру (классу, группе) были более похожи друг на друга, чем на объекты других кластеров. В отечественной литературе синонимом термина "кластерный анализ" является термин "таксономия". В иностранной литературе под таксономией традиционно понимается классификация видов животных и растений.

Все рассмотренные далее методы могут быть использованы как для классификации объектов, так и для классификации признаков

Виды используемых в кластерном анализе мер сходства и различия перекликаются с философской дилеммой: "ищите сходство" или "ищите различие". Меры сходства для кластерного анализа могут бы" следующих видов:

Мера сходства типа расстояния (функции расстояния), называемая также мерой различия. В этом случае объекты считаются тем более похожими, чем меньше расстояние между ними, поэтому некоторые авторы называют меры сходства типа расстояния мерами различия.

Мера сходства типа корреляции, называемая связью, является мерой, определяющей похожесть объектов. В этом случае объекты считаются тем более похожими, чем больше связь между ними. Меры могут быть легко приведены к предыдущему типу, как показано ниже.

Фактически, кластерный анализ является не столько обычным статистическим методом, сколько "набором" различных алгоритмов "распределения объектов по кластерам". Следует понимать, что кластерный анализ определяет "наиболее возможно значимое решение". Поэтому проверка статистической значимости в действительности здесь неприменима, даже в случаях, когда известны p-уровни (как, например, в методе K средних).

 

Иерархическое дерево

 

Рассмотрим горизонтальную древовидную диаграмму. Диаграмма начинается с каждого объекта в классе (в левой части диаграммы). Теперь представим себе, что постепенно (очень малыми шагами) вы "ослабляете" ваш критерий о том, какие объекты являются уникальными, а какие нет. Другими словами, вы понижаете порог, относящийся к решению об объединении двух или более объектов в один кластер.

В результате, связывается вместе всё большее и большее число объектов и объединяется все больше и больше кластеров, состоящих из все сильнее различающихся элементов. Окончательно, на последнем шаге все объекты объединяются вместе.

Меры расстояния

 

Объединение или метод древовидной кластеризации используется при формировании кластеров несходства или расстояния между объектами. Эти расстояния могут определяться в одномерном или многомерном пространстве.

Евклидово расстояние. Это, по-видимому, наиболее общий тип расстояния. Оно попросту является геометрическим расстоянием в многомерном пространстве и вычисляется следующим образом:

.

Евклидово расстояние (и его квадрат) вычисляется по исходным, а не по стандартизованным данным. Это обычный способ его вычисления, который имеет определенные преимущества (например, расстояние между двумя объектами не изменяется при введении в анализ нового объекта, который может оказаться выбросом). Тем не менее, на расстояния могут сильно влиять различия между осями, по координатам которых вычисляются эти расстояния.

Квадрат евклидова расстояния. Иногда может возникнуть желание возвести в квадрат стандартное евклидово расстояние, чтобы придать большие веса более отдаленным друг от друга объектам. Это расстояние вычисляется следующим образом:

.

Расстояние городских кварталов (манхэттенское расстояние). Это расстояние является просто средним разностей по координатам. Для этой меры влияние отдельных больших разностей (выбросов) уменьшается (так как они не возводятся в квадрат). Манхэттенское расстояние вычисляется по формуле:

.

Расстояние Чебышева. Это расстояние может оказаться полезным, когда желают определить два объекта как "различные", если они различаются по какой-либо одной координате (каким-либо одним измерением). Расстояние Чебышева вычисляется по формуле: .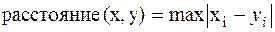

Степенное расстояние. Иногда желают прогрессивно увеличить или уменьшить вес, относящийся к размерности, для которой соответствующие объекты сильно отличаются. Это может быть достигнуто с использованием степенного расстояния. Степенное расстояние вычисляется по формуле:

.

где r и p - параметры, определяемые пользователем. Несколько примеров вычислений могут показать, как "работает" эта мера. Параметр p ответственен за постепенное взвешивание разностей по отдельным координатам, параметр r ответственен за прогрессивное взвешивание больших расстояний между объектами. Если оба параметра r и p, равны двум, то это расстояние совпадает с расстоянием Евклида.

Процент несогласия. Эта мера используется в тех случаях, когда данные являются категориальными. Это расстояние вычисляется по формуле:

расстояние(x,y) = (Количество x<>y_i)/n_i

 

Правила объединения или связи

 

На первом шаге, когда каждый объект представляет собой отдельный кластер, расстояния между этими объектами определяются выбранной мерой.

Одиночная связь (метод ближайшего соседа). Этот метод является самым простым для понимания из иерархических агломеративных методов кластерного анализа. Метод начинает процесс классификации с поиска и объединения двух наиболее похожих объектов в матрице сходства. На следующем этапе находятся два очередных наиболее похожих объекта, и процедура повторяется до полного исчерпания матрицы сходства.

В процессе кластеризации методом ближней связи явно прослеживается образование цепочек объектов. Таким образом, для выделения кластеров после окончания процесса кластеризации требуется задаться некоторым пороговым уровнем сходства, на котором выделяется число кластеров, большее единицы. Процедура не всегда обнаруживает такое свойство, как образование одного большого кластера на последнем этапе кластеризации, и часто заканчивается явным разделением всех предъявленных объектов на кластеры. После проведения классификации рекомендуется визуализировать результаты кластеризации путем построения дендрограммы. Для большого числа объектов такая визуализация является единственным способом получить представление об общей конфигурации объектов.

Полная связь (метод наиболее удаленных соседей). В этом методе расстояния между кластерами определяются наибольшим расстоянием между любыми двумя объектами в различных кластерах (т. е. "наиболее удаленными соседями"). Этот метод обычно работает очень хорошо, когда объекты происходят на самом деле из реально различных "рощ". Если же кластеры имеют в некотором роде удлиненную форму или их естественный тип является "цепочечным", то этот метод непригоден.

Невзвешенное попарное среднее. В этом методе расстояние между двумя различными кластерами вычисляется как среднее расстояние между всеми парами объектов в них. Метод эффективен, когда объекты в действительности формируют различные "рощи", однако он работает одинаково хорошо и в случаях протяженных ("цепочного" типа) кластеров.

Взвешенное попарное среднее. Метод идентичен методу невзвешенного попарного среднего, за исключением того, что при вычислениях размер соответствующих кластеров (т. е. число объектов, содержащихся в них) используется в качестве весового коэффициента. Поэтому предлагаемый метод должен быть использован (скорее даже, чем предыдущий), когда предполагаются неравные размеры кластеров.

Невзвешенный центроидный метод. В этом методе расстояние между двумя кластерами определяется как расстояние между их центрами тяжести.

Взвешенный центроидный метод (медиана). Этот метод идентичен предыдущему, за исключением того, что при вычислениях используются веса для учёта разницы между размерами кластеров (т. е. числами объектов в них). Поэтому, если имеются (или подозреваются) значительные отличия в размерах кластеров, этот метод оказывается предпочтительнее предыдущего.

Метод Варда (Уорда). Этот метод отличается от всех других методов, поскольку он использует методы дисперсионного анализа для оценки расстояний между кластерами. Метод минимизирует сумму квадратов (SS) для любых двух (гипотетических) кластеров, которые могут быть сформированы на каждом шаге. В целом метод представляется очень эффективным, однако он стремится создавать кластеры малого размера.

 

Метод K средних

 

В общем случае метод K средних строит ровно K различных кластеров, расположенных на возможно больших расстояниях друг от друга.

С вычислительной точки зрения, вы можете рассматривать этот метод как дисперсионный анализ "наоборот". Программа начинает с K случайно выбранных кластеров, а затем изменяет принадлежность объектов к ним, чтобы: (1) - минимизировать изменчивость внутри кластеров, и (2) - максимизировать изменчивость между кластерами. Данный способ аналогичен методу "дисперсионный анализ наоборот" в том смысле, что критерий значимости в дисперсионном анализе сравнивает межгрупповую изменчивость с внутригрупповой при проверке гипотезы о том, что средние в группах отличаются друг от друга. В кластеризации методом K средних программа перемещает объекты (т.е. наблюдения) из одних групп (кластеров) в другие для того, чтобы получить наиболее значимый результат при проведении дисперсионного анализа (ANOVA).

Обычно, когда результаты кластерного анализа методом K средних получены, можно рассчитать средние для каждого кластера по каждому измерению, чтобы оценить, насколько кластеры различаются друг от друга. В идеале вы должны получить сильно различающиеся средние для большинства, если не для всех измерений, используемых в анализе. Значения F-статистики, полученные для каждого измерения, являются другим индикатором того, насколько хорошо соответствующее измерение дискрими-нирует кластеры.

 

Выбор адекватного теста для того, чтобы сравнивать показатели достаточно сложное мероприятие, поскольку Вам необходимо выбирать между двумя семействами тестов - параметрическими и непараметрическими.

Выбор между параметрическими и непараметрическими

тестами: легкая ситуация.

Выбор между параметрическими и непараметрическими тестами иногда достаточно прост: Вы должны четко выбрать параметрический тест, если Вы уверены, что Ваши данные были получены как выборка из популяции, которая соответствует нормальному распределению. Вы должны определенно выбирать непараметрический тест в следующих ситуациях:

· Результат является ранговым значением или оценочным значением и популяция явно не имеет нормального распределения. Примеры могут включать ранжирование студентов, шкалу Апгара, которая измеряет здоровье новорожденных (измеряется на шкале от 0 до 10 и все значения являются целыми), визуальную аналоговую шкалу боли (которая измеряется на непрерывной шкале где 0 - это отсутствие боли и 10 - это непереносимая боль), и так называемая звездочная шкала, которая используется критиками при оценке фильмов и ресторанов (*неплохо, ***** прекрасно).

· Некоторые значения очень резко отличаются от остальных, то есть слишком высокие или слишком низкие для измерений. Даже если популяция является Гауссовой невозможно анализировать такие данные параметрическим тестом, поскольку Вы не знаете всех значений. Использование с этими данными непараметрического теста достаточно простое: Вы присваиваете тем значениям, которые являются слишком низкими для того, чтобы их можно было измерить произвольное, но очень небольшое значение, и для очень больших значений Вы присваиваете произвольное, но очень большое значение, а затем выполняете непараметрический тест. Поскольку непараметрические тесты базируются только на информации о ранговом положении значений, тот факт, что Вы не знаете точных значений этих показателей уже не будет Вам сильно мешать.

· Данные, которые достаточно точно измерены, но Вы уверены, что популяция не распределяется в соответствии с нормальным законом. Если данные не получены из Гауссовского распределения, тогда Вы должны вначале подумать нельзя ли трансформировать значение так, чтобы оно превратилось в Гауссовское. Например, Вы можете взять логарифм или величину обратную всем значениям. Часто имеются биологические или химические причины (также как и статистические) для того, чтобы выполнить ту или иную трансформацию.

Выбор между параметрическими и непараметрическими

тестами: сложные случаи.

Не всегда легко определить является ли выборка из Гауссовой популяции. Обратите внимание на следующие положения:

· Если Вы имеете большое количество наблюдений (100 или более) Вы можете посмотреть на распределение данных и совершенно четко будет видно насколько оно соответствует знаменитой колоколообразной кривой нормального распределения. Формальный статистический тест (тест Колмогорова-Смирнова) может использоваться для того, чтобы проанализировать вопрос насколько распределение данных отличается от Гауссова распределения. Когда у Вас имеется только небольшое количество наблюдений, очень сложно принять решение о том, следуют ли данные Гауссовому распределению и формальные тесты также имеют очень маленькую статистическую мощность для того, чтобы найти различие между Гауссовым и не Гауссовым распределением.

· Вы должны посмотреть на предыдущие данные. Помните, что то что Вас интересует - это распределение популяции в целом, а не распределение Вашей выборки. Принимая решение о том, является ли Ваше распределение нормальным, посмотрите на все имеющиеся данные, а не только на данные нынешнего эксперимента.

· Обратите внимание на источники разброса, когда разброс идет как результат суммы различных источников и ни один из источников не является основным источником разброса, у Вас скорее всего будет распределение Гаусса. Когда люди сомневаются, то некоторые выбирают параметрические тесты (поскольку они не уверены, что нарушается допущение о следовании нормальному закону распределения), а другие выбирают непараметрические тесты (поскольку они не уверены, что выполняются допущения о соответствии распределения Гаусса.

Выбор между параметрическим и непараметрическим тестом: насколько это на самом деле влияет на результат?

На самом деле надо ли задумываться о выборе параметрического или непараметрического теста? Ответ зависит от размере выборки. Есть четыре вещи о которых следует подумать:

· Большая выборка. Что произойдет, если Вы используете параметрический тест с данными, которые были получены на Гауссовой популяции? Центральная предельная теорема гарантирует, что параметрический тест будет хорошо работать с большими выборками если даже популяция, из которой была получены выборка, не является Гауссовой. Иными словами параметрические тесты являются устойчивыми к отклонению от Гауссового распределения в том случае, если выборка достаточно большая. Проблема, однако, заключается в том, что невозможно сказать насколько большая является достаточно большой и это все зависит от природы определенного не Гауссового распределения. Однако в том случае, если популяция не является действительно очень странной, Вы по всей вероятности, можете достаточно спокойно выбирать параметрический тест, если у Вас имеется по крайней мере, две дюжины наблюдений в каждой группе.

· Большая выборка. Что произойдет, если Вы будете использовать непараметрический тест с данными из Гауссовой популяции? Непараметрические тесты работают достаточно хорошо в большими выборками Гауссовой популяции. Р-значение имеет тенденцию быть немножко великоватым, но различия очень небольшие. Иными словами непараметрические тесты лишь ненамного менее мощны, чем параметрические тесты на больших выборках.

· Небольшие выборки. Что произойдет, если Вы будете использовать параметрический тест с данными от не Гауссовой популяции? Вы не можете полагаться на центральную предельную теорему и поэтому р-значение будет неправильным.

· Небольшие выборки. Что произойдет, если Вы будете использовать непараметрические тесты с данными из Гауссовой популяции? В этом случае р-оценка имеет тенденцию быть крайне высокой. Непараметрический тест не обладает достаточно высокой статистической мощностью на небольших выборках.

Поэтому большие наборы данных не представляют большой проблемы. Обычно достаточно легко сказать пришли ли данные из Гауссовой популяции, хотя на самом деле это уже не столь важно, поскольку непараметрические тесты достаточно мощны, а параметрические тесты устойчивы. Небольшие наборы данных как раз и являются основной проблемой. Достаточно сложно сказать пришли ли данные из Гауссовой популяции, однако это очень важно. Непараметрические тесты при небольшом объеме данных недостаточно мощны, а параметрические тесты не являются устойчивыми.

Одно или двухсторонняя p-оценка?

Для большинства статистических тестов Вы должны выбирать хотите ли Вы рассчитать одно- или двух- стороннюю р-оценку. Различия между одно и двухсторонней р-оценкой обсуждалось ранее, а теперь давайте вспомним про эти различия в контексте t-теста. Р-оценка подсчитывается для нулевой гипотезы что две популяции имеют одинаковые значения средних и любые различия между двумя выборочными средними являются следствием случайных факторов. Если эта нулевая гипотеза справедлива односторонняя р-оценка - это вероятность того, что две выборочных средних будут различаться настолько много, насколько было обнаружено или (даже больше) в направлении, которое было указано гипотезой за счет случайных факторов, даже если среднее в популяции в целом на самом деле равное. Двухсторонняя р-оценка также включает вероятность того, что выборочные средние могут различаться таким же образом и в противоположном направлении, то есть другая группа имеет большее среднее. Двухсторонняя р-оценка таким образом выше, чем односторонняя.

Односторонняя р-оценка является адекватной когда Вы можете точно установить (и перед сбором любых данных), что здесь нет никаких различий между средними либо различия будут идти в направлении, которое Вы можете указать с самого начала (то есть Вы можете указать в какой группе будут более высокие средние значения). Если Вы не можете указать направления или любые различия, прежде чем начинать сбор данных, тогда более адекватным будет использовать двухстороннюю р-оценку. Если Вы сомневаетесь, выбирайте двухстороннюю р-оценку.

Если Вы выбираете односторонний тест, Вы должны сделать это до сбора каких бы то ни было данных и Вам необходимо установить направление Вашей экспериментальной гипотезы. Если данные пойдут в другую сторону, Вы должны будете согласиться на то, что эти различия ассоциация или корреляция является следствием действия случайных факторов вне зависимости от того, насколько серьезными получаются эти различия. Если Вы будете заинтересованы (даже немного) тем, насколько данные могут пойти в "неправильном" направлении, то тогда Вы должны использовать двухстороннюю р-оценку. По этим и другим причинам, которые обсуждались ранее, я бы рекомендовал Вам, чтобы Вы всегда анализировали только двухстороннюю р-оценку.

Парный или непарный тест?

Когда Вы сравниваете две группы, Вам необходимо решить использовать или не использовать парный тест. Когда Вы сравниваете три или более группы, термин парные уже не используется, используется термин повторные измерения.

Вы должны использовать парный тест, когда Вы сравниваете группы, в которых индивидуальные значения не связаны друг с другом и не соотнесены один с другим. Выбирайте парный тест или тесты с повторными измерениями, когда значения представляют собой повторные измерения у одного и того же субъекта (до и после вмешательства) или измерения, сделанные на специально подобранных парах наблюдений. Парные или тесты с повторными измерениями также подходят для повторных экспериментов в лаборатории, которые выполняются в разное время каждый раз со своим собственным контролем.

Вы должны подбирать парный тест, когда значение в одной группе больше коррелирует с определенными значениями в другой группе, чем со случайными значениями в другой группе. Адекватным является выбирать парный тест только в том случае, если субъекты были собраны в пары до начала сбора данных. Вы не можете создавать парный тест на данных, которые Вы собрали ранее, а сейчас анализируете.

Тест Фишера или хи-квадрат?

Когда Вы анализируете таблицы сопряженности с двумя строками и двумя столбцами, Вы можете использовать либо точный тест Фишера, либо тест хи-квадрат. Тест Фишера является более хорошим выбором, поскольку он всегда дает точное значение р-оценки. Хи-квадрат легче подсчитывать, но он дает только примерное значение р-оценки. Если компьютер делает все расчеты, Вы должны выбирать тест Фишера за исключением ситуации, когда Вы предпочитаете хи-квадрат на основе того, что он более хорошо известен. Вы должны совершенно четко избегать хи-квадрат в том случае, если количество наблюдений (любое число ниже 6). Когда значение больше р-оценки, которые получаются в результате использования теста хи-квадрат и теста Фишера будут очень похожи друг на друга.

Тест хи-квадрат рассчитывает примерные p-значения и поправка Йетса на непрерывность предназначена для того, чтобы сделать это приближение лучше. Без поправки Йетса p-значения слишком небольшие, однако если коррекция заходит слишком далеко, результирующая p-оценка оказывается слишком большой. Статистики дают различные рекомендации по отношению к поправке Йетса. Когда имеется большая выборка, то поправка Йетса не приводит к серьезным различиям. Если Вы выбираете тест Фишера, p-значение является точным и в этой ситуации поправка Йетса на непрерывность не является необходимой.

Регрессия или корреляция?

Линейная регрессия и корреляция являются очень похожими друг на друга и их легко спутать. В некоторых ситуациях имеет смысл выполнять оба типа расчета. Рассчитывайте линейную корреляцию, если Вы измеряете как Х, так и Y у каждого обследованного и хотите оценить насколько хорошо они связаны друг с другом. Выбирайте Пирсоновский (параметрический коэффициент) коэффициент корреляции если Вы предполагаете, что Х и Y были выбраны из Гауссовой популяции. В другом случае выбирайте непараметрический коэффициент корреляции Спирмена. Не рассчитывайте коэффициент корреляции или доверительный интервал если Вы сами воздействовали на значение переменной Х. Рассчитывайте линейную регрессию только в том случае, если одна из переменных Х по всей вероятности является предшественником или причиной изменения другой переменной Y. Совершенно четко выбирайте линейную регрессию, если Вы сами воздействовали на переменную Х. В линейной регрессии очень серьезные различия получаются в зависимости от того, какая переменная обозначается Х, а какая переменная обозначается Y, поскольку подсчеты при помощи линейной регрессии не симметричны по отношению к Х и Y. Если Вы поменяете местами эти две переменные, Вы можете получить другую регрессионную линию. В противоположность этому линейный коэффициент корреляции симметричный по отношению к Х и Y, и если Вы поменяете местами маркеры для Х и Y, Вы получите тот же самый корреляционный коэффициент.

Вопросы для самопроверки:

 

1. Перечислите требования, которые необходимы для вычисления критерия Стьюдента, критерия c² Пирсона.

2. Что такое метод наименьших квадратов?

3. Сформулируйте в примерах задачу из области Вашей будущей специализации, при решении которой необходимо вычислить: а) регрессионное уравнение б) частные коэффициенты корреляции

4. Сформулируйте в содержательных понятиях задачи из области специализации, связанные с анализом динамических рядов.

5. Сформулируйте в содержательных понятиях задачи из области специализации, связанные с анализом циклических явлений.

6. На какие компоненты могут быть разложены динамические ряды и, какую информацию об исследуемом процессе несут эти компоненты?

7. Как можно определить какое из регрессионных уравнений наилучшим способом описывает тренд динамического ряда.

8. По каким показателям осуществляется объединение объектов в кластеры.

РАЗДЕЛ IV. РАБОТА С ПРОГРАММОЙ EASYSTATISTICS

Общие сведения о программе EasyStatistics

 

В программе 3 основных страницы: "Новый файл", "Выборка" и "Результаты".

 

В окне "Новый файл" проводятся основные операции с базой:

1. Создание нового файла

2. Редактирование

3. Изменение названий переменных и случаев.

4. Сохранение файла

5. Установка фильтра

 

Внимание: все расчеты осуществляются по окну "Выборка"

В случае если открывается уже ранее созданный файл окна "Файл данных" и "Выборка" совпадают. Это значит, что для вычисления любой статистики будут использованы все переменные и случаи. Если необходимы только часть из них, необходимо воспользоваться кнопкой "Фильтр".

 

Окно "Выборка" предназначено для

1. Просмотра текущих переменных и случаев, используемых в анализе

2. Сохранения части основной базы в виде отдельного файла

 

Окно "Результаты" предназначено для

1. Просмотра результатов

2. Печати результатов

3. Сохранения результатов в виде текстового файла или файла MS Excel

4. Копирования результатов в буфер обмена

Внимание: кнопка печать работает только в окне "Результаты"

 

Статистические методы:

% P-?

Описательная статистика Частотный анализ Таблицы 2х2 Сравнение независимых выборок Сравнение связанных выборок Дисперсионный анализ Корреляционный анализ Множественная регрессия Проверка типа распределения эмпирических данных Вероятностный калькулятор

Создание новой базы данных

 

Для создания новой базы данных необходимо выбрать пункт меню Файл→Новый или нажать кнопку в панели инструментов.

В появившемся окне потребуется ввести количество переменных и случаев

После нажатия кнопки "Создать" в окне "Новый файл" формируется таблица нужных размеров. По умолчанию все переменные называются VAR1, VAR2 и т.д.

Для того, чтобы изменить названия переменных и случаев надо выбрать пункт меню "Правка→Редактировать названия переменных и случаев" или кнопку

После окончания редактирования рекомендуется снова нажать кнопку или пункт меню "Правка→Завершить редактирование".

 

Внимание: Называть переменные можно по-русски, но если потом потребуется перевод файла в другие статистические программы, то рекомендуется ввод английскими буквами и до 8 символов (например, вместо "Возраст" можно написать "Age" или "Vozrast").

 

Теперь заполняются данные:

 

Внимание: В том случае если на какой-то объект исследования нет данных, то просто оставляется пустое место

 

После окончания ввода базу данных желательно сохранить "Файл → сохранить как". Поддерживаются форматы:

1. est – основной формат EasyStatistics

2. sta – формат Statistica 5.0-5.5

3. xls – формат MS Excel

4. txt – текстовый формат с разделителями табуляции

 

Внимание: Программа никак не отслеживает сохранены данные или нет. Если закрыть программу, не сохранив файл, то потеряются все набранные данные.

Работа с файлами

 

Для того, чтобы открыть ранее сделанную базу данных нужно выбрать пункт меню "Файл→ открыть" или нажать на кнопку .

Поддерживаются форматы:

1. est – основной формат EasyStatistics

2. sta – формат Statistica 5.0-5.5

3. * – текстовый формат с разделителями табуляции

 

 

Копирование и вставка данных

 

Копирование (кнопка ) возможно в любом из окон «Файл», «Выборка», «Результаты», вставка () только в окне «Файл».

 

Внимание: Иногда требуется перенести в программу значительные объемы данных, например, из MS Excel. В этом случае программа может зависнуть. Поэтому, в зависимости от ситуации рекомендуется выполняить копирование-вставку несколькими частями или, если есть необходимость перенести в программу целый лист, необходимо сохранить его в MS Excel в формате «текстовый формат с разделителями табуляции», а затем открыть в EasyStatistics.

 

Если есть необходимость копировать или вставлять названия переменных или случаев, перед началом операции необходимо выбрать пункт меню "Правка→Редактировать названия переменных и случаев" или кнопку .

 

Работа с фильтрами

 

Вся статистическая обработка выполняется для данных, находящихся в окне «Выборка». В случае если открывается уже ранее созданный файл окна "Файл данных" и "Выборка" совпадают. Это значит, что для вычисления любой статистики будут использованы все переменные и случаи. Если необходимы только часть из них, необходимо воспользоваться кнопкой или воспользоваться пунктом меню "Таблица→Фильтр".

Переменные пишутся цифрами (1 2 7-10) или выделяются мышкой.

 

Внимание: Для выбора переменных по-порядку (например, 1-10) используется клавиша Shift + Мышка, для выделения в разнобой (например, 1 3 5-7) используется клавиша Ctrl + Мышка.

 

Выбор случаев – это математическое выражение, поэтому во избежание путаницы перед номером переменной используется приставка v (или V).

 

Окно для ввода переменных   Окно для написания условия

 

Примеры выражений:

(допустим, на рисунке переменная Пол закодирована следующим образом: 1 – девушки, 2 – юноши, переменные Ботаника и История содержат оценки по этим предметам на экзамене)

1. v5=1 (отобрать только девушек)

2. v5=1 & v6=5 (отобрать девушек с оценкой «отлично» по ботанике)

3. v5=1 & v6=5 & v7=5 (отобрать девушек с оценкой «отлично» по ботанике и истории)

4. v5=1 & v6=5! v7=5 (отобрать девушек с оценкой «отлично» по ботанике или истории)

5. v6=5! v6=4 (отобрать всех лиц с отличными и хорошими оценками по ботанике)

6. (v6+v7)/2>=4 (отобрать всех лиц со средним баллом по ботанике и истории не менее 4.

7. (v6+v7)/2>=4 & v5=2 (отобрать юношей со средним баллом по ботанике и истории не менее 4.

8. v0<30

⇐ Предыдущая1234

Поделиться:

Воспользуйтесь поиском по сайту: