 |
методом узловых потенциалов
|
|
|
|
к выполнению расчетно-графического
задания №1
Красноярск
ИПК СФУ
 2010
2010
УДК 621.3
Печатается по решению редакционно-издательского
совета университета
Расчет линейных электрических цепей постоянного тока: метод. указания к выполнению расчетно-графического задания №1 / сост. А. Ф. Копылов. – Красноярск: ИПК СФУ, 2010. – 47 с.
Методические указания содержат варианты заданий, теоретические сведения и методику расчета электрических цепей постоянного тока, необходимые для выполнения расчетно-графического задания №1.
Предназначены для студентов направления 210300.62 «Радиотехника».
© Сибирский федеральный
университет, 2010
Учебно-методическое издание
РАСЧЕТ ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ
ЦЕПЕЙ ПОСТОЯННОГО ТОКА
Методические указания
к выполнению расчетно-графического
задания №1
Составители:
Редактор
Компьютерная верстка
 |
Подписано в печать 21.09.09.
Печать плоская.
Формат 60х84/16.
Бумага офсетная.
Усл. печ. л. 3,72.
Тиражэкз.
Заказ
Издательско-полиграфический комплекс
Сибирского федерального университета
660041, г. Красноярск, пр. Свободный, 82а
Отпечатано в типографии ИПК СФУ
 660041, г. Красноярск, пр. Свободный, 82а
660041, г. Красноярск, пр. Свободный, 82а 
1. ЗАДАНИЕ И ВЫБОР ВАРИАНТА ДЛЯ ЕГО ВЫПОЛНЕНИЯ
Целью настоящего расчетно-графического задания (РГЗ) является изучение студентами основных методов расчета сложных электрических цепей. С этой целью студенту поручается рассчитать токи во всех ветвях схемы сложной электрической цепи. Схема электрической цепи, в ветвях которой следует рассчитать токи, приведена на рис. 1.1. Эта схема является универсальной для всех вариантов РГЗ и различается по вариантам количеством и местом включения источников ЭДС и тока. Студент перерисовывает схему рис. 1.1 и воспроизводит на схеме только те элементы, которые содержатся в его варианте. Номером варианта являются последние две цифры зачетной книжки или студенческого билета (от 1 до 100). В соответствии с этим номером из табл. 1.1следует произвести выбор данных, необходимых для выполнения задания.
|
|
|

Рис. 1.1. Электрическая схема цепи, в которой следует рассчитать токи
| Номер вари-анта | Величины сопротивлений  – –  , Ом , Ом
| Величины источников ЭДС  – – 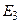 , В , В
| |||||||

| 
| 
| 
| 
| 
| 
| 
| 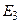
| |
| - | |||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | - | |||||||
| - | - | - | |||||||
| - | |||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | |||||||||
| - | - | - | |||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | |||||||||
| - | - | ||||||||
| - | |||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | - | |||||||
| - | |||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | - | |||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | - | |||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - |
|
|
|
Таблица 1.1
| Номер вари-анта | Величины источников ЭДС  – –  , В , В
| Величины источников тока  – –  , А , А
| |||||||

| 
| 
| 
| 
| 
| 
| 
| 
| |
| - | - | - | - | - | - | - | |||
| - | - | - | - | - | - | ||||
| - | - | - | - | - | - | ||||
| - | - | - | - | - | |||||
| - | - | - | - | - | |||||
| - | - | - | - | - | - | - | |||
| - | - | 1,5 | - | - | - | - | |||
| - | - | - | - | 2,5 | - | - | |||
| - | - | - | - | - | - | ||||
| - | - | - | - | - | 3,5 | - | |||
| - | - | - | - | 4,5 | - | - | |||
| - | - | - | - | - | |||||
| - | - | - | - | - | - | ||||
| - | - | - | - | - | |||||
| - | - | - | - | - | - | ||||
| - | - | - | - | - | |||||
| - | - | - | - | 3,5 | - | - | |||
| - | - | 3,5 | - | - | 2,5 | - | |||
| - | - | 4,5 | - | - | 1,5 | - | |||
| - | - | 5,5 | - | - | - | - | |||
| - | - | - | - | 5,5 | - | - | |||
| - | - | - | - | - | 6,5 | - | |||
| - | - | - | - | - | - | 7,5 | |||
| - | - | - | - | - | - | ||||
| - | - | - | - | - | - | ||||
| - | - | - | - | - | |||||
| - | - | - | - | - | - | - | |||
| - | - | - | - | - | - | ||||
| - | - | - | - | - | - | ||||
| - | - | 6,5 | - | - | - | - | |||
| - | - | - | 7,5 | - | - | - | |||
| - | - | - | 8,5 | - | - | ||||
| - | - | - | - | 9,5 | - | - | |||
| - | - | - | - | - | - | ||||
| - | - | - | - | - | - | ||||
| - | 1,5 | - | - | - | - | ||||
| - | - | - | 2,5 | - | - | - | |||
| - | - | - | - | 2,5 | - | - | |||
| - | - | - | - | 3,5 | - | - | |||
| - | - | - | - | - | - | ||||
| - | - | - | - | - | - | ||||
| - | - | - | - | - | - |
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | - | |||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | |||||||||
| - | - | - | |||||||
| - | - | ||||||||
| - | - | ||||||||
| - | |||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | - | |||||||
| - | - | - | |||||||
| - | - | - | |||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | - | |||||||
| - | - | - | |||||||
| - | - | - | |||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | - | |||||||
| - | - | - | |||||||
| - | - | ||||||||
| - | |||||||||
| - | |||||||||
| - | |||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - |
Продолжение табл. 1.1
|
|
|
| - | - | - | - | - | 1,5 | - | |||
| - | - | - | - | - | - | 2,5 | |||
| - | - | 3,5 | - | - | - | - | |||
| - | - | - | 4,5 | - | - | - | |||
| - | - | - | 5,5 | - | - | 2,5 | |||
| - | - | - | - | 2,2 | - | - | |||
| - | - | - | - | - | 2,4 | - | |||
| - | - | - | - | - | - | 2,6 | |||
| - | - | - | - | - | 2,8 | - | |||
| - | - | - | - | - | - | ||||
| - | - | - | - | - | - | - | |||
| - | - | - | - | 1,5 | - | - | |||
| - | - | - | - | 3,2 | - | 2,5 | - | ||
| - | - | - | 4,4 | - | - | - | 3,5 | ||
| - | - | 4,6 | - | - | - | 4,5 | - | ||
| - | - | - | 0,1 | - | 1,2 | - | - | ||
| - | - | - | - | 2,2 | - | 0,2 | - | ||
| - | - | - | 3,2 | - | 0,3 | - | - | ||
| - | - | 4,2 | - | 0,4 | - | - | - | ||
| - | 1,6 | 0,5 | - | - | - | - | |||
| - | - | - | 0,6 | 1,8 | - | ||||
| - | - | - | 1,9 | - | 0,7 | - | - | ||
| - | - | - | - | 2,1 | - | 0,8 | - | ||
| - | - | - | - | 2,2 | - | - | 0,9 | ||
| - | - | - | 2,3 | - | - | - | |||
| - | 2,4 | - | - | - | - | ||||
| - | - | - | 1,1 | - | - | ||||
| - | - | - | 1,2 | - | - | - | |||
| - | - | 1,3 | - | - | - | - | |||
| - | - | - | 1,4 | - | - | - | |||
| - | - | - | - | 1,5 | - | 2,5 | - | ||
| - | - | - | - | 1,6 | 1,5 | ||||
| - | - | 2,5 | - | - | - | - | |||
| - | - | - | - | 3,5 | - | - | - | ||
| - | - | - | - | 4,5 | - | - | |||
| - | - | - | - | - | 1,5 | - | - | ||
| - | - | - | 1,5 | - | - | - | |||
| - | - | - | - | 2,5 | - | - | 0,2 | ||
| - | - | - | 3,5 | - | - | 0,1 | - | ||
| - | - | - | 4,5 | - | 0,3 | - | - | ||
| - | - | - | - | 0,4 | - | - | |||
| - | - | - | 0,5 | - | - | - | |||
| - | - | 0,6 | - | - | - | - | |||
| - | - | 0,7 | - | - | - | - | |||
| - | - | - | 0,8 | - | - | - |
|
|
|
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - | ||||||||
| - | - |
Для выбранного варианта задания выполнить следующее:
1. Составить на основании законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы.
2. Определить токи во всех ветвях схемы методом контурных токов.
3. Определить токи во всех ветвях схемы методом узловых потенциалов.
4. Результаты расчета токов, проведенного двумя методами, свести в таблицу и сравнить их.
5. Рассчитать любой ток методом эквивалентного генератора.
6. Составить баланс мощностей в исходной схеме.
7. Начертить потенциальную диаграмму для любого замкнутого контура, включающего обе ЭДС.
2. РАСЧЕТ ВЕЛИЧИН ТОКОВ НЕПОСРЕДСТВЕННЫМ ПРИМЕНЕНИЕМ ЗАКОНОВ КИРХГОФА, МЕТОДАМИ КОНТУРНЫХ ТОКОВ, УЗЛОВЫХ ПОТЕНЦИАЛОВ И МЕТОДОМ ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА
В нашем расчетно-графическом задании мы рассматриваем следующие способы расчета токов во всех ветвях заданной схемы:
|
|
|
– расчет токов путем применения законов Кирхгофа;
– расчет токов методом контурных токов;
– расчет токов методом узловых потенциалов;
– расчет токов методом эквивалентного генератора.
Окончание табл. 1.1
| - | - | - | 0,9 | - | - | - | |||
| - | - | - | - | 1,1 | - | 1,5 | |||
| - | - | - | - | - | 1,2 | - | 1,2 | ||
| - | - | - | - | - | 1,3 | - | 1,3 | ||
| - | - | - | - | - | - | 1,4 | - | ||
| - | - | - | 2,1 | - | - | 1,5 | - | ||
| - | - | - | 2,2 | - | - | - | |||
| - | - | - | - | - | 2,3 | - | |||
| - | - | - | 2,5 | - | - | - | |||
| - | - | - | - | - | 3,1 | - | |||
| - | - | - | - | - | - | 3,2 |
2.1. Анализ (расчет) сложных электрических цепей применением уравнений Кирхгофа
Задача анализа (расчета) цепи – это нахождение токов во всех ее ветвях; при этом величины сопротивлений, источников ЭДС и тока и сама схема электрической цепи должны быть известны.
Сложная электрическая цепь – это такая цепь, рассчитать токи в которой невозможно с помощью закона Ома и требуется применение специальных методов расчета.
Разберем порядок расчета (анализа) сложной электрической цепи применением законов Кирхгофа и получим необходимые расчетные формулы в общем виде. Для этого в качестве типовой анализируемой схемы электрической цепи примем схему, показанную на рис. 1.1. Положим, что в этой схеме установлены источники ЭДС  и
и  , а также источники тока
, а также источники тока  и
и  . Тогда типовая схема, показанная на рис. 1.1 примет вид, показанный на рис. 2.1.
. Тогда типовая схема, показанная на рис. 1.1 примет вид, показанный на рис. 2.1.
Для составления уравнений по законам Кирхгофа следует обозначить направления токов во всех ветвях схемы, а также все узлы в схеме. Поскольку до того, как токи во всех ветвях схемы не буду рассчитаны, неизвестными являются не только величины искомых токов, но и их направления, направления токов в ветвях схемы рис. 2.1 придется выбрать произвольно. После того, как токи будут определены, они окажутся либо со знаком “плюс”, либо со знаком “минус”. Этот знак покажет, что, при обозначении направления тока в той или иной ветви схемы, мы либо случайно угадали его истинное направление (если ток получился с плюсом), либо не угадали (если ток получился с минусом). Для анализа цепи знак, с которым получился искомый ток, значения не имеет – пусть будет хоть “плюс”, хоть “минус”, но менять направление тока в схеме, если при расчете он получился отрицательным, не следует, чтобы далее при работе с этой схемой не ошибиться в других расчетах. То есть, отрицательное значение постоянного тока в той или иной ветви электрической цепи, получившееся при расчете, означает только то, что ток в этой ветви течет в направлении, противоположном выбранному в начале расчета схемы, и этот факт не требует изменения направления при проведении дальнейших расчетов.

Рис. 2.1. Пример схемы сложной электрической цепи
На рис. 2.2 показана та же схема, что и на рис. 2.1, но с обозначенными на ней узлами, а также направлениями и величинами токов в ветвях (их удобно называть токами ветвей).
Направления токов ветвей на рис. 2.2 обозначены стрелками на проводах ветвей, а величины токов ветвей – символами  ,
,  ,
,  ,
,  ,
,  ,
,  с индексами, соответствующими индексам сопротивлений, расположенных в этих ветвях. Малыми буквами латинского алфавита
с индексами, соответствующими индексам сопротивлений, расположенных в этих ветвях. Малыми буквами латинского алфавита  ,
,  ,
,  и
и  обозначены все узлы – точки соединения трех и более ветвей. Потенциалы этих узлов имеют обозначения
обозначены все узлы – точки соединения трех и более ветвей. Потенциалы этих узлов имеют обозначения  ,
,  ,
,  и
и  , соответственно.
, соответственно.
После того, как в анализируемой схеме обозначены токи ветвей, узлы и их потенциалы, запишем уравнения первого и второго законов Кирхгофа для этой схемы.

Рис. 2.2. Эквивалентная схема сложной электрической цепи с обозначенными на ней узлами 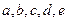 , а также токами ветвей
, а также токами ветвей 
По первому закону Кирхгофа можно составить, в общей сложности, четыре уравнения – для узлов a, b, c и d. Запишем эти уравнения, условившись, что втекающие токи (то есть, направленные в узел), имеют знак «плюс», а вытекающие токи (то есть, направленные из узла) – знак «минус». Можно было взять и обратные этим направления токов – вытекающие из узла с «плюсом», втекающие в узел – с «минусом». Для расчетов это значения не имеет и на результатах не сказывается, так как означает домножение правой и левой частей уравнений первого закона Кирхгофа на  .
.
Тогда для узлов a, b, c и d уравнения первого закона Кирхгофа будет иметь следующий вид, соответственно:
 . (2.1)
. (2.1)
 , (2.2)
, (2.2)
 , (2.3)
, (2.3)
 . (2.4)
. (2.4)
Сравнив между собой уравнения (2.1) – (2.4), отметим, что первые три из них, записанные для узлов a, b и c (2.1) – (2.3), отличаются друг от друга, по крайней мере, одним током. Четвертое же уравнение (2.4) первого закона Кирхгофа для узла d (2.4) содержит все токи, уже имеющиеся в уравнениях для узлов a, b и c. Этой означает, что уравнение первого закона Кирхгофа для узла d (2.4) является линейно зависимым от уравнений первого закона Кирхгофа для узлов a (2.1), b (2.2) и c (2.3). При этом узлы a, b и c называют независимыми, а узел d – зависимым. Соответственно этому, уравнения первого закона Кирхгофа для схемы рис. 2.2 для узлов a, b и c (2.1), (2.2), (2.3), соответственно, будут линейно независимы, а уравнение первого закона Кирхгофа для узла d – линейно зависимым от уравнений первого закона Кирхгофа для других узлов схемы рис. 2.2. Таким образом, количество независимых узлов в анализируемой схеме электрической цепи оказывается на один меньше общего числа узлов в этой схеме, а количество независимых уравнений, которые можно составить по первому закону Кирхгофа, на одно меньше общего числа уравнений, которые можно составить по этому закону для анализируемой схемы.
По этой причине уравнение для узла d (2.4) можно исключить из системы уравнений первого закона Кирхгофа, что эквивалентно заземлению этого узла. Тогда система уравнений, составленных по первому закону Кирхгофа для этой цепи примет вид:
 . (2.5)
. (2.5)
Поскольку общее число уравнений для нахождения токов во всех шести ветвях схемы рис. 2.2 должно быть также не менее шести, для получения решения к трем уравнениям, составленным по первому закону Кирхгофа (2.5), требуется составить ещё три уравнения. Это можно сделать, составив три уравнения второго закона Кирхгофа для схемы рис. 2.2. Для составления этих трёх уравнений перерисуем схему рис. 2.2 анализируемой цепи и представим её в виде, показанном на рис. 2.3. Обозначения, принятые на схеме рис. 2.3 соответствуют обозначениям, принятым на схеме рис. 2.2, но, в отличие от схемы рис. 2.2, на рис. 2.3 прерывистыми овалами со стрелками обозначены направления обхода контуров схемы анализируемой цепи. Эти направления выбраны по часовой стрелке и означают, что все падения напряжений на элементах контура, который мы будем обходить, и которые совпадут по направлению с направлением обхода контура, будут иметь знак «плюс» в левой части уравнения второго закона Кирхгофа, а при несовпадении направления обхода с направлением падения напряжения на данном элементе контура, будут иметь знак «минус» в левой части уравнения второго закона Кирхгофа, включая и источники тока и ЭДС, если в правой части уравнения второго закона Кирхгофа при этом записан ноль. Кроме того, на схеме рис. 2.3 расставлены полярности и обозначены падения напряжений для каждого элемента цепи, включая источники ЭДС и тока. Полярности падений напряжений соответствуют принятым ранее направлениям токов  в ветвях, то есть, для сопротивлений падение напряжения направлено согласно с направлением тока (от плюса к минусу), а для источников ЭДС и тока падение напряжения противоположно току внутри источника. Направления обхода контуров можно было выбрать и против часовой стрелки – как и при выборе направлений токов в узлах при составлении уравнений первого закона Кирхгофа, это означает всего лишь домножение правой и левой частей уравнений второго закона Кирхгофа на
в ветвях, то есть, для сопротивлений падение напряжения направлено согласно с направлением тока (от плюса к минусу), а для источников ЭДС и тока падение напряжения противоположно току внутри источника. Направления обхода контуров можно было выбрать и против часовой стрелки – как и при выборе направлений токов в узлах при составлении уравнений первого закона Кирхгофа, это означает всего лишь домножение правой и левой частей уравнений второго закона Кирхгофа на  .
.

Рис. 2.3. Эквивалентная схема сложной электрической цепи с обозначенными на ней направлениями обхода контуров (по часовой стрелке)
Количество уравнений, составленных по второму закону Кирхгофа для анализируемой схемы рис. 2.3, должно быть равно числу независимых контуров. Число независимых контуров в схеме рис. 2.3 равно трём, так как, если составить для трёх обозначенных прерывистыми овалами со стрелками контуров этой схемы уравнения по второму закону Кирхгофа (первый контур  , второй контур
, второй контур  , третий контур
, третий контур  ), окажется, что, в этих уравнениях будут фигурировать все возможные падения напряжений, имеющиеся на рис. 2.3. Все остальные возможные обходы контуров (например, обход по контуру
), окажется, что, в этих уравнениях будут фигурировать все возможные падения напряжений, имеющиеся на рис. 2.3. Все остальные возможные обходы контуров (например, обход по контуру  , контуру
, контуру  ), являются линейно зависимыми и не могут быть приняты для системы уравнений второго закона Кирхгофа.
), являются линейно зависимыми и не могут быть приняты для системы уравнений второго закона Кирхгофа.
Ещё один важный момент, который следует подробно рассмотреть, связан с тем, что часть ветвей анализируемой схемы содержит источники тока. В анализируемой схеме рис. 2.3 это первая ветвь, образованная сопротивлением  , источником ЭДС
, источником ЭДС  и источником тока
и источником тока  , а также шестая ветвь, образованная сопротивлением
, а также шестая ветвь, образованная сопротивлением  и источником тока
и источником тока  . Учет этих источников тока не сразу ясен при составлении уравнений второго закона Кирхгофа для контуров, поэтому есть смысл разобрать этот вопрос подробнее.
. Учет этих источников тока не сразу ясен при составлении уравнений второго закона Кирхгофа для контуров, поэтому есть смысл разобрать этот вопрос подробнее.
Если преобразовать ветви с источниками тока в эквивалентные им ветви с источниками ЭДС, то источники ЭДС  и
и  , эквивалентные источникам тока
, эквивалентные источникам тока  и
и  , можно легко включить в уравнения второго закона Кирхгофа по тому же принципу, как и источники ЭДС
, можно легко включить в уравнения второго закона Кирхгофа по тому же принципу, как и источники ЭДС  и
и  . Преобразовать же источники тока в источники ЭДС можно, используя принцип эквивалентных преобразований: различные электрические схемы эквивалентны друг другу, если на внешних относительно этих схем узлах токи и напряжения остаются неизменными.
. Преобразовать же источники тока в источники ЭДС можно, используя принцип эквивалентных преобразований: различные электрические схемы эквивалентны друг другу, если на внешних относительно этих схем узлах токи и напряжения остаются неизменными.
Проведем преобразование источника тока в эквивалентный ему источник ЭДС на примере шестой ветви. Изобразим на рис. 2.4, а фрагмент схемы цепи рис. 2.3, включающий шестую ветвь, который заключен между узлами a и c. На рис. 2.4, б покажем цепь с источником ЭДС, эквивалентную исходной шестой ветви.
В исходной схеме замещения источника тока рис. 2.4, а, падение напряжения


